Проектирование реляционных БД на основе принципов нормализации
Даталогическое проектирование
В реляционных БД даталогическое или логическое проектирование приводит к разработке схемы БД, то есть совокупности схем отношений, которые адекватно моделируют абстрактные объекты предметной области и семантические связи между этими объектами. Основой анализа корректности схемы являются так называемые функциональные зависимости между атрибутами БД. Некоторые зависимости между атрибутами отношений являются нежелательными из-за побочных эффектов и аномалий, которые они вызывают при модификации БД. При этом под процессом модификации БД мы понимаем внесение новых данных в БД или удаление некоторых данных из БД, а также обновление значений некоторых атрибутов.
Однако этап логического или даталогического проектирования не заканчивается проектированием схемы отношений. В общем случае в результате выполнения этого этапа должны быть получены следующие результирующие документы:
- Описание концептуальной схемы БД в терминах выбранной СУБД.
- Описание внешних моделей в терминах выбранной СУБД.
- Описание декларативных правил поддержки целостности базы данных.
- Описание процедур поддержки семантической целостности базы данных.
Однако перед тем как описывать построенную схему в терминах выбранной СУБД, нам надо выстроить эту схему. Именно этому процессу и посвящен данный раздел. Мы должны построить корректную схему БД, ориентируясь на реляционную модель данных.
Корректной назовем схему БД, в которой отсутствуют нежелательные зависимости между атрибутами отношений.
Процесс разработки корректной схемы реляционной БД называется логическим проектированием БД.
Проектирование схемы БД может быть выполнено двумя путями:
- путем декомпозиции (разбиения),когда исходное множество отношений, входящих в схему БД заменяется другим множеством отношений (число их при этом возрастает), являющихся проекциями исходных отношений;
- путем синтеза,то есть путем компоновки из заданных исходных элементарных зависимостей между объектами предметной области схемы БД.
Классическая технология проектирования реляционных баз данных связана с теорией нормализации, основанной на анализе функциональных зависимостей между атрибутами отношений. Понятие функциональной зависимости является фундаментальным в теории нормализации реляционных баз данных. Мы определим его далее, а пока коснемся смысла этого понятия. Функциональные зависимости определяют устойчивые отношения между объектами и их свойствами в рассматриваемой предметной области. Именно поэтому процесс поддержки функциональных зависимостей, характерных для данной предметной области, является базовым для процесса проектирования.
Процесс проектирования с использованием декомпозиции представляет собой процесс последовательной нормализации схем отношений, при этом каждая последующая итерация соответствует нормальной форме более высокого уровня и обладает лучшими свойствами по сравнению с предыдущей.
Каждой нормальной форме соответствует некоторый определенный набор ограничений, и отношение находится в некоторой нормальной форме, если удовлетворяет свойственному ей набору ограничений.
В теории реляционных БД обычно выделяется следующая последовательность нормальных форм:
- первая нормальная форма (1NF);
- вторая нормальная форма (2NF);
- третья нормальная форма (3NF);
- нормальная форма Бойса—Кодда (BCNF);
- четвертая нормальная форма (4NF);
- пятая нормальная форма, или форма проекции-соединения (5NF или PJNF).
Основные свойства нормальных форм:
- каждая следующая нормальная форма в некотором смысле улучшает свойства предыдущей;
- при переходе к следующей нормальной форме свойства предыдущих нормальных форм сохраняются.
В основе классического процесса проектирования лежит последовательность переходов от предыдущей нормальной формы к последующей. Однако в процессе декомпозиции мы сталкиваемся с проблемой обратимости,то есть возможности восстановления исходной схемы. Таким образом, декомпозиция должна сохранять эквивалентность схем БД при замене одной схемы на другую.
Схемы БД называются эквивалентными,если содержание исходной БД может быть получено путем естественного соединения отношений, входящих в результирующую схему, и при этом не появляется новых кортежей в исходной БД.
При выполнении эквивалентных преобразований сохраняется множество исходных фундаментальных функциональных зависимостей между атрибутами отношений.
Функциональные зависимости определяют не текущее состояние БД, а все возможные ее состояния, то есть они отражают те связи между атрибутами, которые присущи реальному объекту, который моделируется с помощью БД.
Поэтому определить функциональные зависимости по текущему состоянию БД можно только в том случае, если экземпляр БД содержит абсолютно полную информацию (то есть никаких добавлений и модификации БД не предполагается). В реальной жизни это требование невыполнимо, поэтому набор функциональных зависимостей задает разработчик, системный аналитик, исходя из глубокого системного анализа предметной области.
Приведем ряд основных определений.
Функциональной зависимостью набора атрибутов В отношения R от набора атрибутов A того же отношения, обозначаемой как R.A -> R.B или A -> B
называется такое соотношение проекций R[A] и R[B], при котором в каждый момент времени любому элементу проекции R[A] соответствует только один элемент проекции R[B], входящий вместе с ним в какой-либо кортеж отношения R.
Функциональная зависимость R.A -> R.B называется полной,если набор атрибутов B функционально зависит от A и не зависит функционально от любого подмножества A, то есть R.A -> R.B называется полной, если:
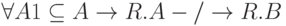 ,
,
что читается следующим образом:
для любого A1, являющегося подмножеством А, R.B функционально не зависит от R.A, в противном случае зависимость R.A -> R.B называется неполной.
Функциональная зависимость R.A -> R.B называется транзитивной, если существует набор атрибутов С такой, что:
- С не является подмножеством А.
- С не включает в себя B.
- Существует функциональная зависимость R.A -> R.C.
- Не существует функциональной зависимости R.C -> R.A.
- Существует функциональная зависимость R.C -> R.B.
Возможным ключом отношения называется набор атрибутов отношения, который полностью и однозначно (функционально полно) определяет значения всех остальных атрибутов отношения, то есть возможный ключ — это набор атрибутов, однозначно определяющий кортеж отношения, и при этом при удалении любого атрибута из этого набора его свойство однозначной идентификации кортежа теряется.
А может ли быть ситуация, когда отношение не имеет возможного ключа? Давайте вспомним определение отношения: отношение — это подмножество декартова произведения множества доменов. И в полном декартовом произведении все наборы значений различны, тем более в его подмножестве. Значит, обязательно для каждого отношения всегда существует набор атрибутов, по которому можно однозначно определить кортеж отношения. В вырожденном случае это просто полный набор атрибутов отношения, потому что если мы зададим для всех атрибутов конкретные значения, то, по определению отношения, мы получим только один кортеж.
В общем случае в отношении может быть несколько возможных ключей.
Среди всех возможных ключей отношения обычно выбирают один, который считается главным и который называют первичным ключом отношения.
Неключевым атрибутом называется любой атрибут отношения, не входящий в состав ни одного возможного ключа отношения.
Взаимно-независимые атрибуты — это такие атрибуты, которые не зависят функционально один от другого.
Если в отношении существует несколько функциональных зависимостей, то каждый атрибут или набор атрибутов, от которого зависит другой атрибут, называется детерминантом отношения.
Для функциональных зависимостей как фундаментальной основы проекта БД были проведены исследования, позволяющие избежать избыточного их представления. Ряд зависимостей могут быть выведены из других путем применения правил, названных аксиомами Армстронга, по имени исследователя, впервые сформулировавшего их. Это три основных аксиомы:
- Рефлексивность: если В является подмножеством А, то А -> B
- Дополнение: если А->B, то A.C -> B.C
- Транзитивность: если A -> B и B -> C, то A -> C.
Доказано, что данные правила являются полными и исчерпывающими, то есть, применяя их, из заданного множества функциональных зависимостей можно вывести все возможные функциональные зависимости.
Множество всех возможных функциональных зависимостей, выводимое из заданного набора исходных функциональных зависимостей, называется его замыканием.
Отношение находится в первой нормальной форме тогда и только тогда, когда на пересечении каждого столбца и каждой строки находятся только элементарные значения атрибутов.
В некотором смысле это определение избыточно, потому что собственно оно определяет само отношение в теории реляционных баз данных. Однако в силу исторически сложившихся обстоятельств и для преемственности такое определение первой нормальной формы существует и мы должны с ним согласиться. Отношения, находящиеся в первой нормальной форме, часто называют просто нормализованными отношениями. Соответственно, ненормализованные отношения могут интерпретироваться как таблицы с неравномерным заполнением, например таблица "Расписание", которая имеет вид:
| Преподаватель | День недели | Номер пары | Название дисциплины | Тип занятий | Группа |
|---|---|---|---|---|---|
| Петров В. И. | Понед. | 1 | Теор. выч. проц. | Лекция | 4906 |
| Вторник | 1 | Комп. графика | Лаб. раб.. | 4907 | |
| Вторник | 2 | Комп. графика | Лаб. раб | 4906 | |
| Киров В. А. | Понед. | 2 | Теор. информ. | Лекция | 4906 |
| Вторник | 3 | Пр-е на С++ | Лаб. раб. | 4907 | |
| Вторник | 4 | Пр-е на С++ | Лаб. раб. | 4906 | |
| Серов А. А. | Понед. | 3 | Защита инф. | Лекция. | 4944 |
| Среда | 3 | Пр-е на VB | Лаб. раб | 4942 | |
| Четверг | 4 | Пр-е на VB | Лаб. раб. | 4922 |
Здесь на пересечении одной строки и одного столбца находится целый набор элементарных значений, соответствующих набору дней, перечню пар, набору дисциплин, по которым проводит занятия один преподаватель.
Для приведения отношения "Расписание" к первой нормальной форме необходимо дополнить каждую строку фамилией преподавателя.
| Преподаватель | День недели | Номер пары | Название дисциплины | Тип занятий | Группа |
|---|---|---|---|---|---|
| Петров В. И. | Понед. | 1 | Теор. выч. проц. | Лекция | 4906 |
| Петров В. И. | Вторник | 1 | Комп. графика | Лаб. раб.. | 4907 |
| Петров В. И. | Вторник | 2 | Комп. графика | Лаб. раб | 4906 |
| Киров В. А. | Понед. | 2 | Теор. информ. | Лекция | 4906 |
| Киров В. А. | Вторник | 3 | Пр-е на С++ | Лаб. раб. | 4907 |
| Киров В. А. | Вторник | 4 | Пр-е на С++ | Лаб. раб. | 4906 |
| Серов А. А. | Понед. | 3 | Защита инф. | Лекция. | 4944 |
| Серов А. А. | Среда | 3 | Пр-е на VB | Лаб. раб | 4942 |
| Серов А. А. | Четверг | 4 | Пр-е на VB | Лаб. раб. | 4922 |
