Методы проектирования логических моделей реляционных баз данных. Декомпозиция и синтез отношений
Пример. Применение алгоритма синтеза
Пример иллюстрирует работу алгоритма на каждом из его этапов.
- Если
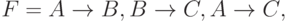 то
то  может быть удалена.
может быть удалена. - Пусть
 тогда или A, или B могут быть удалены из
тогда или A, или B могут быть удалены из 
 или
или  выводится из F1 следующим образом:
Из
выводится из F1 следующим образом:
Из  (по аддитивности); из
(по аддитивности); из 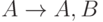 и
и  (по транзитивности).
(по транзитивности). - Пусть
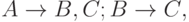 тогда С может быть удалена из
тогда С может быть удалена из  Из
Из 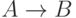 и
и  (по транзитивности); из
(по транзитивности); из 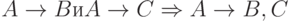 (по аддитивности).
(по аддитивности). - Пусть
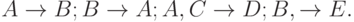 Тогда так как
Тогда так как  то имеется одна группа
то имеется одна группа  Так как
Так как  (по расширяемости и аддитивности), то другая группа есть
(по расширяемости и аддитивности), то другая группа есть 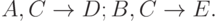
- Из
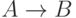 и
и  Так как
Так как 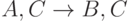 принадлежит к другой группе, чем
принадлежит к другой группе, чем 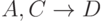 и
и 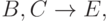 то последние ФЗ могут быть заменены на
то последние ФЗ могут быть заменены на 
- Имеем

- Пусть с=(A;B;A,B).
 Сдвигаем A,B в правую часть с и получаем с' = (A;B). Тогда
Сдвигаем A,B в правую часть с и получаем с' = (A;B). Тогда 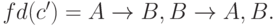 A,B может быть удалена из с, так как они есть в левой части с'.
Так как
A,B может быть удалена из с, так как они есть в левой части с'.
Так как 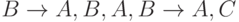 могут быть выведены из
могут быть выведены из  то с может быть заменена на с'.
то с может быть заменена на с'. - Пусть

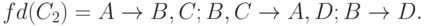 D удаляется из
D удаляется из  и
и 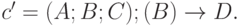
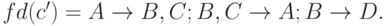 Так как
Так как  может быть выведена из
может быть выведена из  то С2 может быть заменена на С'.
то С2 может быть заменена на С'. - Пусть
 Тогда первое отношение есть ABCD c ключом (A,{B,C}) ; второе отношение есть BD с ключом {B} ; третье отношение есть FG с ключом {F,G}.
Тогда первое отношение есть ABCD c ключом (A,{B,C}) ; второе отношение есть BD с ключом {B} ; третье отношение есть FG с ключом {F,G}.
Выводы
- В рамках теории реляционных баз данных предлагается два основных подхода к построению логических моделей баз данных: метод декомпозиции и метод синтеза схем отношений.
- Метод декомпозиции основывается на разбиении некоторого универсального отношения на два или более отношений с помощью реляционной операции проекции.
- Метод синтеза основывается на обработке исходного множества ФЗ предметной области базы данных.
- Метод декомпозиции нагляден, достаточно просто реализуется в инструментальных CASE -средствах проектирования, но имеет ряд потенциальных недостатков, связанных с потерей данных при соединениях и с потерей ФЗ.
- Метод синтеза не приводит к потерям ФЗ, но имеет ряд потенциальных угроз потери информации при соединениях и обладает высокой вычислительной стоимостью.
- Предлагается ряд технических приемов по преодолению потенциальных недостатков в обоих подходах, позволяющих строить эффективные логические модели данных.
- На практике при построении логической модели реляционной базы данных целесообразно комбинировать оба подхода, отдавая предпочтение методу декомпозиции.
Создание логической модели реляционной базы данных методом декомпозиции: преобразование ER -диаграмм в отношения базы данных
Практика проектирования реляционных баз данных методом декомпозиции отношений показала ряд его недостатков, связанных с потерей данных при соединениях и с потерей ФЗ. Однако метод декомпозиции достаточно прост для понимания, нагляден, легко реализуется в инструментальных CASE -средствах проектирования и в настоящее время является наиболее часто применяемым при проектировании баз данных.
Для построения логических моделей реляционных баз данных методом декомпозиции сформулирован ряд правил, получивших название правила преобразования ER-диаграмм в отношения базы данных. Правила позволяют исключить потенциальные недостатки метода декомпозиции и нацелены на приведения схемы отношений базы данных к нормальным формам.
Рассмотрим правила преобразования на примере базы данных о преподавателях, читающих лекции в институте. Сущность Преподаватель соотносится с сущностью Предмет посредством связи Читает. При этом возможны следующие варианты поведения данной предметной области:
- каждый преподаватель читает только один курс, и каждый курс читается только одним преподавателем, т.е. классы принадлежности обеих сущностей являются обязательными;
- каждый преподаватель читает только один курс, и каждый курс читается не более чем одним преподавателем, т.е. класс принадлежности первой сущности является обязательным, а второй сущности - необязательным;
- каждый преподаватель читает не более одного курса, и каждый курс читается не более чем одним преподавателем, т.е. классы принадлежности обеих сущностей не являются обязательными;
- каждый преподаватель читает не более одного курса, а каждый курс читается только одним преподавателем.
Возможны варианты с иной степенью связи, например когда каждый преподаватель может читать несколько курсов.
Каждый из этих вариантов может быть представлен ER-диаграммой. Однако следует помнить, что каждая ER-диаграмма представляет свой собственный набор правил поведения предметной области и только одна из них может быть истинной в каждый момент времени.
Если степень бинарной связи определена, то предварительные отношения могут быть получены путем просмотра нескольких альтернатив и выбора варианта, наиболее подходящего с точки зрения правил предметной области и личных предпочтений проектировщика. Определяющими признаками выбора одного из альтернативных вариантов представления отношения являются степень связи и класс принадлежности сущности.
Сформулируем первое правило.
Правило 1. Если степень бинарной связи 1:1 и класс принадлежности обеих сущностей является обязательным, то требуется построение только одного отношения. При этом первичным ключом отношения может быть ключ любой сущности.
Исходное отношение является одновременно и конечным отношением.
Пример.
ПРЕПОДАВАТЕЛЬ (Табельный_номер, Фамилия, Предмет,
Количество_часов)Это правило может быть применено для первого варианта поведения предметной области, когда исходное отношение не требует декомпозиции, так как не содержит избыточных данных и нуль-значений.
Сформулируем второе правило.
Правило 2. Если степень бинарной связи 1:1 и класс принадлежности одной сущности является обязательным, а другой сущности - не обязательным, то требуется построение двух отношений - по одному на каждую сущность. При этом первичным ключом каждого отношения является ключ его сущности, а ключ сущности с необязательным классом принадлежности добавляется в отношение для сущности с обязательным классом принадлежности в качестве атрибута (миграция ключа).
Пример.
Исходное отношение:
ПРЕПОДАВАТЕЛЬ_1 (Табельный_номер, Фамилия, Предмет,
Количество_часов)
Результирующие отношения:
ПРЕПОДАВАТЕЛЬ_2 (Табельный_номер, Фамилия, Предмет)
ПРЕДМЕТЫ (Предмет, Количество_часов)Это правило может быть применено во втором варианте, когда исходное отношение уже требует декомпозиции. Исходное отношение ПРЕПОДАВАТЕЛЬ_1 содержит проблему нуль-значений: данные о предметах, которые не читаются в данный момент, не могут быть внесены в базу данных.
Результирующее отношение ПРЕПОДАВАТЕЛЬ_2 не имеет проблемы нуль-значений. В результирующем отношении ПРЕДМЕТЫ эта проблема исключается: для предмета, который в данный момент не читается, определяется специальное непустое значение по умолчанию. Миграция ключа необходима для восстановления исходного отношения. Таким образом, миграция ключа в методе декомпозиции представляет собой перенос первичного ключа одного отношения в другое отношение для предотвращения потери данных при соединении.
