Методы проектирования логических моделей реляционных баз данных. Декомпозиция и синтез отношений
Алгоритм метода синтеза отношений
В данном разделе приводится лишь некоторый обзор алгоритма синтеза отношений.
Мы уже рассматривали примеры декомпозиции с потерей ФЗ. Причиной потери ФЗ является некоторая ФЗ 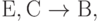 которая не может быть исключена из множества F-зависимостей, связанных с получаемыми отношениями R1 или R2. Таким образом, суть проблемы сводится к нарушению замкнутости реляционных операций над ФЗ на полученной схеме базы данных. Для того чтобы ее решить, необходимо пополнить минимальное покрытие ФЗ, или, как говорят, усилить минимальное покрытие.
которая не может быть исключена из множества F-зависимостей, связанных с получаемыми отношениями R1 или R2. Таким образом, суть проблемы сводится к нарушению замкнутости реляционных операций над ФЗ на полученной схеме базы данных. Для того чтобы ее решить, необходимо пополнить минимальное покрытие ФЗ, или, как говорят, усилить минимальное покрытие.
На пути решения этой проблемы было бы неплохо усилить все ФЗ, связав их с уникальными ключами, скажем, описывая для них уникальные индексы. Тогда можно контролировать целостность базы данных. Для этого нужно усилить минимальное покрытие. Грубо говоря, усиливаемость минимального покрытия означает, что выделено множество первичных ключей и все ФЗ из минимального покрытия пересмотрены в призме этого множества с точки зрения выводимости ФЗ рассматриваемой базы данных.
Введем определение.
Определение 4. Реляционная база данных называется полной, если:
- все ФЗ усилены ключами;
- все отношения находятся в 3НФ;
- не существует варианта базы данных с меньшим числом схем, удовлетворяющим вышеперечисленным свойствам.
Почти всегда в предметной области базы данных можно выделить набор отношений, обладающих свойством полноты. Доказана теорема [Мейер], что существует алгоритм, который выводит полную базу данных из множества заданных ФЗ.
Поскольку такой алгоритм строит схему базы данных непосредственно из заданного набора ФЗ, он называется алгоритмом синтеза базы данных. При этом на первый план выступает проблема правильного представления отношения с заданной схемой своими проекциями, т.е. соединения по результирующей схеме базы данных могут оказаться ложными. Однако если минимальное покрытие исходного набора ФЗ будет усилено, то подобного явления можно избежать.
Пример. Универсальный ключ и ложные соединения
Пусть отношение R имеет кортежи:
Случай 1. Отсутствие ложных соединений
Разбиение на отношения
не дает ложных соединений.
Случай 2. Наличие ложных соединений
Разбиение на отношения
дает ложные соединения
ABCD
Поскольку
то решить проблему можно, введя универсальный ключ {A,C}. Тогда можно добавить в исходную схему отношение
AC
и выполнить соединение отношений AB, BCD и AC, которое восстановит исходное отношение ABCD.
Заметим, что атрибут А выступает в качестве ключа практически во всех ФЗ. Выделенный или добавленный атрибут, обладающий подобным свойством, называется универсальным ключом. Таким образом, решение проблемы ложных соединений заключается в добавлении подсхемы, которая содержит универсальный ключ, и выполнении соединения с ее использованием.
Теперь можно перейти к обзору алгоритма синтеза реляционной базы данных.
Теоретически показано, что для того, чтобы синтезировать полную базу данных, необходимо построить кольцевое минимальное покрытие для исходного набора ФЗ.
Введем некоторые обозначения. Составной ФЗ называется ФЗ: 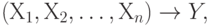 где Y может быть пусто. С каждой составной ФЗ можно связать набор ФЗ:
где Y может быть пусто. С каждой составной ФЗ можно связать набор ФЗ: 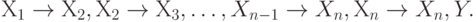 Пусть С - множество составных ФЗ, fd(C) - множество всех ФЗ, связанных с ФЗ из С.
Пусть С - множество составных ФЗ, fd(C) - множество всех ФЗ, связанных с ФЗ из С.
В принятых обозначениях основные этапы алгоритма синтеза отношений приведены ниже.
Алгоритм поэтапного синтеза отношений
Вход: F - множество ФЗ предметной области базы данных
Выход: схема полной базы данных
Этап 1. Нахождение неизбыточного покрытия F1 для F
Для каждой ФЗ из F проверяется, может ли данная ФЗ быть выведена из оставшихся ФЗ. Если да, то ФЗ удаляется. Этап завершается после перебора всех ФЗ из F. В результате выполнения этапа получается множество ФЗ F1.
Этап 2. Сокращение слева элементов F1
Удаляются последовательно один за другим атрибуты из левых частей ФЗ F1 ; проверяется, может ли полученная ФЗ быть выведена из исходных ФЗ F1. Если да, то исходная ФЗ заменяется на новую ФЗ. Этап завершается после перебора всех ФЗ F1. В результате получается множество ФЗ F2.
Этап 3. Сокращение справа элементов F2
Удаляются последовательно один за другим атрибуты ФЗ из правых частей ФЗ F2 ; проверяется, может ли исходная ФЗ быть выведена из полученной ФЗ и имеющихся ФЗ F2. Если да, то исходная ФЗ заменяется на новую ФЗ. Этап завершается после перебора всех ФЗ F2. В результате получается множество ФЗ F3.
На этом сокращение ФЗ закончено. Избыточность отсутствует. Необходимо приступать к построению минимального покрытия.
Этап 4. Разделение F3 на классы эквивалентности по правым частям
Строится разбиение F3 на группы: две ФЗ принадлежат одной и той же группе тогда и только тогда, когда их правые части эквивалентны. В результате получается множество классов эквивалентности ФЗ 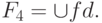
Этап 5. Удаление в классах эквивалентности избыточных ФЗ
Для всех пар ФЗ fdi и fdj из одной и той же группы проверяется, может ли ФЗ левой стороны fdj от правой стороны fdj быть выведена из этой группы ФЗ. Если да, то из fdj ФЗ удаляется и добавляется в правую часть этой ФЗ к правой fdi. Новая ФЗ будет находиться в той же группе, что и исходная ФЗ. В результате получается минимальное число ФЗ F5, покрывающих F3.
Этап 6. Получение классов эквивалентности по левым частям F5 и составных ФЗ C1
Для каждого множества ФЗ с эквивалентными левыми частями из F5 создается составная ФЗ 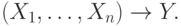 Если какой-либо атрибут из Y есть в Xi, то этот атрибут удаляется. В результате получается множество составных ФЗ С1.
Если какой-либо атрибут из Y есть в Xi, то этот атрибут удаляется. В результате получается множество составных ФЗ С1.
Этап 7. Удаление избыточных зависимостей из С1
Для каждой составной ФЗ из С1 и для каждого атрибута Xi из левой части С сдвигаются атрибуты в правую часть. В результате получается множество составных ФЗ С'. Если fd(C') эквивалентно fd(C1), то С1 заменяется на С'. В результате получается множество ФЗ С2.
Этап 8. Формирование кольцевого минимального покрытия
Для каждой составной ФЗ c из С2 и каждого атрибута A из правой части c удаляется атрибут А. В результате получается С', состоящее из с'. Если fd(C') эквивалентно fd(C2), то С2 заменяется на С'. В результате получается множество ФЗ С3.
Этап 9. Формирования схемы полной базы данных
Для каждой составной ФЗ с из С3 формируется таблица атрибутов, которые появляются в с. Ключами для этой таблицы являются Хi из левой части с. Таблица послужит для усиления ФЗ в F.
Алгоритм поэтапного синтеза отношений обладает хорошей сходимостью, его целесообразно использовать в запрограммированном виде. Для этого можно воспользоваться уже готовой программой, или написать свою программу с учетом специфики своих задач, обратившись к монографии Д. Мейера [3].

