Реляционная модель данных
Разность отношений
Операция разности выполняется над двумя совместными отношениями А и В. Результатом операции разности является отношение С, которое включает в себя кортежи отношения А, отличные от кортежей отношения В. Таким образом, разность отношений можно представить с помощью теоретико-множественной операции разности:
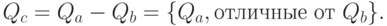
Отметим для дальнейшего, что пересечение отношений можно представить через разность отношений как Qa - (Qa - Qb).
Пример. Разность отношений. Выполним операцию разности отношений КЛИЕНТ_1 и КЛИЕНТ_2. Исходные отношения: КЛИЕНТ_1 (#, Фамилия, Возраст) и КЛИЕНТ_2 (#, Фамилия, Возраст)
Результирующее отношение:
КЛИЕНТ (#, Фамилия, Возраст) = КЛИЕНТ_1 - КЛИЕНТ_2
Декартово произведение отношений
Операция декартова произведения выполняется над двумя произвольными отношениями А и В. Результатом операции декартова произведения является отношение С, степень которого равна сумме степеней исходных отношений, а мощность - произведению мощностей исходных отношений. Таким образом, декартово произведение отношений можно представить с помощью декартова произведения множеств:

Пример. Операция "декартово произведение". Выполним операцию декартова произведения отношений СЛУЖАЩИЕ и МЕДОСМОТР. Исходные отношения: СЛУЖАЩИЕ (#, Фамилия, Пол) МЕДОСМОТР (Процедура, Дата)
Результирующее отношение:
РЕЗУЛЬТАТЫ_МЕДОСМОТРА ( #, Фамилия, Пол, Процедура, Дата ) =
СЛУЖАЩИЙ Х МЕДОСМОТР
| 1 | Иванов | м | ЭКГ | 17.08 |
| 1 | Иванов | м | Анализ крови | 20.08 |
| 1 | Иванов | м | Терапевт | 23.08 |
| 5 | Антонова | ж | ЭКГ | 17.08 |
| 5 | Антонова | ж | Анализ крови | 20.08 |
| 5 | Антонова | ж | Терапевт | 23.08 |
Проекция отношения
Операция проекции выполняется над одним отношением А. Результатом выполнения операции проекции над отношением А является отношение С, которое включает в себя все кортежи отношения А, но только с теми атрибутами, на которые выполняется проекция. Операцию проекции отношения можно представить следующим образом:

Для обозначения проекции в теории реляционных баз данных принято использовать греческую букву 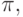 а для обозначения атрибутов, которые участвуют в операции проекции, принято использовать их номера или имена как подстрочные индексы
а для обозначения атрибутов, которые участвуют в операции проекции, принято использовать их номера или имена как подстрочные индексы 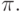 Предполагается, что существует взаимно однозначное соответствие между номерами атрибутов и их именами для данной схемы отношения. Для обозначения атрибутов, которые участвуют в проекции, в формуле выше использованы индексы i1, i2, …, iN, где N - число атрибутов проекции.
Предполагается, что существует взаимно однозначное соответствие между номерами атрибутов и их именами для данной схемы отношения. Для обозначения атрибутов, которые участвуют в проекции, в формуле выше использованы индексы i1, i2, …, iN, где N - число атрибутов проекции.
Таким образом, операция проекции заключается в удалении некоторых атрибутов в исходном отношении Qa и упорядочивании оставшихся атрибутов.
Пример. Проекция отношения. Выполним операцию проекции отношения СОТРУДНИК на атрибуты ОТДЕЛ и ДОЛЖНОСТЬ. Исходное отношение: СОТРУДНИК (#, Фамилия, Отдел, Должность)
| 1 | Иванов | 12 | Инженер |
| 2 | Исаев | 11 | Гл.специалист |
| 3 | Петров | 11 | Инженер |
| 4 | Фролов | 11 | Инженер |
| 5 | Антонова | 12 | Конструктор |
Результирующее отношение:
ДОЛЖНОСТЬ (Отдел, Должность) = p (Отдел, Должность)
Деление отношений
Операция деления выполняется над двумя отношениями А и В, где А - отношение-делимое, а B - отношение-делитель. При этом атрибуты B должны являться подмножеством атрибутов A. Результатом выполнения операции деления является отношение С, которое включает в себя атрибуты отношения А, отличные от атрибутов отношения В, и только те кортежи, декартовы произведения которых с отношением В дают отношение А:

Представление частного отношений через другие алгебраические операции может быть получено следующим образом. Предположим, что  Пусть n и m - арности отношений Qa и Qb, n > m. Тогда разность исходных отношений есть множество кортежей t степени n - m, таких, что для всех кортежей s степени m из Qb, кортеж ts принадлежит Qa. Пусть
Пусть n и m - арности отношений Qa и Qb, n > m. Тогда разность исходных отношений есть множество кортежей t степени n - m, таких, что для всех кортежей s степени m из Qb, кортеж ts принадлежит Qa. Пусть  Тогда
Тогда  есть множество кортежей степени n, не принадлежащих Qa. Каждый из них формируется из n - m первых компонентов кортежа из Qa, за которым следуют компоненты кортежа Qb. Пусть далее
есть множество кортежей степени n, не принадлежащих Qa. Каждый из них формируется из n - m первых компонентов кортежа из Qa, за которым следуют компоненты кортежа Qb. Пусть далее  есть множество кортежей t степени n - m, состоящих из первых n - m компонентов Qa, причем для каждого из них в Qb существует некоторый кортеж s степени m, такой, что ts не принадлежит Qa. Таким образом, разность отношений T - V есть, по определению, частное отношений
есть множество кортежей t степени n - m, состоящих из первых n - m компонентов Qa, причем для каждого из них в Qb существует некоторый кортеж s степени m, такой, что ts не принадлежит Qa. Таким образом, разность отношений T - V есть, по определению, частное отношений 
Пример. Деление отношений. Выполним операцию деления отношения РЕЗУЛЬТАТЫ_МЕДОСМОТРА на отношение МЕДОСМОТР. Исходные отношения: РЕЗУЛЬТАТЫ_МЕДОСМОТРА (#, Фамилия, Пол, Процедура, Дата) МЕДОСМОТР (Процедура, Дата )
| 1 | Иванов | М | ЭКГ | 17.08 |
| 1 | Иванов | М | Анализ крови | 20.08 |
| 1 | Иванов | М | Терапевт | 23.08 |
| 5 | Антонова | Ж | ЭКГ | 17.08 |
| 5 | Антонова | Ж | Анализ крови | 20.08 |
| 5 | Антонова | Ж | Терапевт | 23.08 |
Результирующее отношение:
СЛУЖАЩИЙ (#, Фамилия, Пол) = РЕЗУЛЬТАТЫ_МЕДОСМОТРА / МЕДОСМОТР
