Лекция 11: Численное решение краевых задач для систем обыкновенных дифференциальных уравнений
10.3. Краевая разностная задача Штурма - Лиувилля для обыкновенного дифференциального уравнения второго порядка
Задача Штурма-Лиувилля для обыкновенного дифференциального уравнения второго порядка часто встречается в приложениях. Рассмотрим линейную задачу
![\begin{gather*}
\frac{d}{dt}\left[{g\frac{du}{dt}}\right] + h\frac{du}{dt} + su = f, t \in [a, b], \\
{A\frac{du}{dt} + Bu = D, t = a, } \\
A^{\prime}\frac{du}{dt} + B^{\prime}u = D^{\prime}, t = b, \end{gather*}](/sites/default/files/tex_cache/f02a4c4d53ffb580a794fb94d7bcc0d5.png) |
( 10.1) |
где коэффициенты g, h, s, вообще говоря, являются функциями независимого переменного t.
Для разностной аппроксимации рассматриваемой краевой задачи введем равномерную разностную сетку  и определим на этой сетке сеточную функцию
и определим на этой сетке сеточную функцию 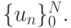
Коэффициент g, вообще говоря, может не иметь первой производной. Такая задача может возникнуть, например, в случае расчета установившегося распределения температуры в задаче стационарной теплопроводности с контактным разрывом. Представим разностную задачу в виде

Контактный разрыв при этом помещается в узел с номером n. В этом случае фактически аппроксимируется тепловой поток через границы ячейки разностной сетки, для уравнения теплопроводности получается консервативная разностная схема — подробнее смотри в лекциях, посвященных численному решению уравнений в частных производных.
Выписанные выше соотношения определяют простейшую разностную схему. Под разностной схемой здесь и ниже понимается совокупность разностных уравнений для определения значений сеточной функции внутри расчетной области, дополненная соответствующими начальными и граничными условиями для этой сеточной функции.
Для определения значений сеточной функции получается СЛАУ с трехдиагональной матрицей
- b0u0 + c0u1 = d0, anun - 1 - bnun + cnun - 1 = dn , n = 1, ..., N - 1, anuN - 1 - bnun = dn,
где
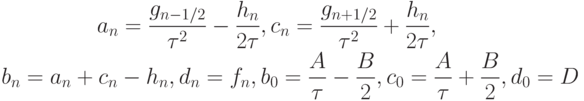
Эта СЛАУ представима в каноническом виде A'u = D, где A' — матрица
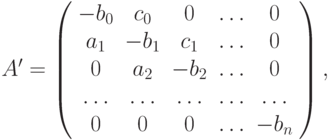
u, d есть векторы - столбцы
D = (d0, d1, ..., dn)T.
Трехдиагональные матрицы часто возникают при численном решении краевых задач как для обыкновенных дифференциальных уравнений, так и для уравнений в частных производных. Ранее матрица подобной структуры встречалась при построении сплайна Шонберга ( "Интерполяция функций" ). Характерная особенность таких матриц заключается в том, что при большой размерности матрица имеет ленточную структуру — все элементы вне ленты (главная диагональ матрицы и по одной диагонали над и под ней) нулевые. В общем случае численное решение СЛАУ n - го порядка требует O(N3) арифметических действий и O(N2) ячеек памяти. В численных методах большую роль играют экономичные алгоритмы, в которых количество арифметических операций пропорционально количеству неизвестных — O(N).
К таким алгоритмам относится метод трехточечной разностной прогонки, появление которого в России связано с именем И.М.Гельфанда, в англоязычной литературе такая прогонка называется алгоритмом Томаса. Экономия памяти очевидна — необходимо хранить только три диагонали исходной матрицы (три одномерных массива). Рассмотрим экономичный вариант метода Гаусса, предназначенный для решения подобных систем.
Решение ищется в виде прогоночного соотношения
un - 1 = pnun + qn, n = 1, ..., N,
где pn и qn — прогоночные коэффициенты, подлежащие определению.
Левое краевое условие также записывается в виде прогоночного соотношения
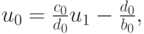
где p1 = c0/ b0, q1 = - d0/ b0 (заметим, что если A > 0 и B < 0, то b0 > c0, 0 < p < 1 ).
Получим рекуррентные формулы, позволяющие последовательно вычислить p2, q2, p3, q3 и т.д. вплоть до pn, qn.
Подставив равенство u n - 1 = pnun + qn в уравнение anun - 1 - bnun + cnu n + 1 = dn, получим an(pnun + qn) - bnun + cnun + 1 = dn, или

Сравнивая эту запись со стандартным видом прогоночного соотношения
un = pn + 1un + 1 + qn + 1,
видим, что для прогоночных коэффициентов должны выполняться равенства
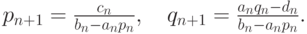
Эти формулы определяют прямой ход прогонки.
Из краевого условия на правом конце отрезка интегрирования anuN - 1 - bNuN = dN и прогоночного соотношения uN - 1 = pNuN + qN находим величину uN.
Далее последовательно вычисляются остальные неизвестные un n = N - 1, ..., 1 un - 1 = pnun + qn. Это — обратный ход алгоритма прогонки.
