НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 3: Численное решение систем линейных алгебраических уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Московский физико-технический институт

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

2.5.2. Влияние ошибок округления на результат численного решения

Будем трактовать суммарный эффект ошибок округления при выполнении одного итерационного шага как возмущение правой части в итерационном процессе

${\mathbf{u}}_k = {\mathbf{Bu}}_{k - 1} + {\mathbf{F}}.$

( 2.19)

Результат вычислений на каждой итерации при наличии ошибок округления представим в виде

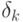${\mathbf{u}}_k^M = {\mathbf{Bu}}_{k - 1}^M + {\mathbf{F}} + {\mathbf{\delta }}_k,$

( 2.20)

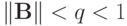где ${\mathbf{\delta }}_k$ — суммарная погрешность округления. Норму разности между реальным и идеальным (т.е. в отсутствии ошибки округления) результатами расчетов получим, вычитая (2.19) из (2.20). Учтем, что $\|\mathbf{B}\| < q < 1$ ,

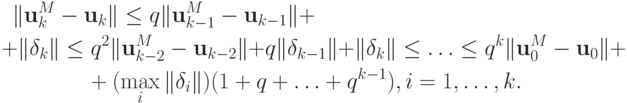
$\begin{multline*} \|{{\mathbf{u}}_k^M - {\mathbf{u}}_k}\| \le q \|{{\mathbf{u}}_{k - 1}^M - {\mathbf{u}}_{k - 1}}\| + \\ + \|{{\mathbf{\delta }}_k}\| \le q^2\|{{\mathbf{u}}_{k - 2}^M - {\mathbf{u}}_{k - 2}}\| + q\|{{\mathbf{\delta }}_{k - 1}}\| + \|{{\mathbf{\delta }}_k}\| \le \ldots \le q^k\|{{\mathbf{u}}_0^M - {\mathbf{u}}_0}\| + \\ + (\max\limits_i \|{{\mathbf{\delta }}_i}\|) (1 + q + \ldots + q^{k - 1}), i = 1, \ldots, k. \end{multline*}$

Так как начальное приближение задано точно 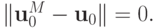$\|{{\mathbf{u}}_0^M - {\mathbf{u}}_0}\| = 0.$ Обозначим 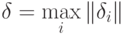$\delta = \max\limits_i \|{{\mathbf{\delta }}_i}\|$ и вычислим сумму членов геометрической прогрессии. Получим

$\|{{\mathbf{u}}_k^M - {\mathbf{u}}_k}\| \le \delta \frac{q^k - 1}{q - 1} \le \frac{\delta }{1 - q}$

, то есть погрешность, вносимая в решение из-за конечной разрядности мантиссы, не зависит от количества итераций. Этот результат является характеристикой устойчивости рассматриваемого вычислительного процесса.

2.5.3. Методы Якоби, Зейделя, верхней релаксации

Представим матрицу $\mathbf{A}$ в виде

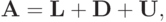$\mathbf{A} = \mathbf{L} + \mathbf{D} + \mathbf{U},$

( 2.21)

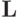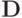где $\mathbf{L}$ и $\mathbf{U}$ — нижняя и верхняя треугольные матрицы с нулевыми элементами на главной диагонали, $\mathbf{D}$ — диагональная матрица. Рассматриваемая СЛАУ может быть переписана в следующем эквивалентном виде:

$\mathbf{Lu}+ \mathbf{Du} + \mathbf{Uu} = \mathbf{f}.$

Построим два итерационных метода 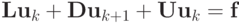$\mathbf{Lu}_k + \mathbf{Du}_{k+1} + \mathbf{Uu}_k = \mathbf{f}$

и

$\mathbf{Lu}_{k+1} + \mathbf{Du}_{k+1} + \mathbf{Uu}_k = \mathbf{f},$

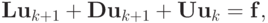
или, соответственно,

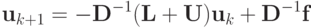${\mathbf{u}}_{k+1} = -\mathbf{D}^{- 1}(\mathbf{L} + \mathbf{U}){\mathbf{u}}_k + \mathbf{D}^{-1}\mathbf{f}$

( 2.22)

и

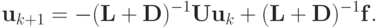${\mathbf{u}}_{k+1} = -(\mathbf{L} + \mathbf{D})^{- 1}{\mathbf{Uu}}_k + (\mathbf{L} + \mathbf{D})^{-1}\mathbf{f}.$

( 2.23)

Очевидно, что эти формулы описывают итерационные процессы вида (2.16), если положить в (2.22)

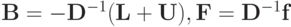
$\mathbf{B} = -\mathbf{D}^{-1}(\mathbf{L} + \mathbf{U}), \mathbf{F} = \mathbf{D}^{-1}\mathbf{f}$

или

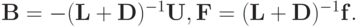
$\mathbf{B} = -(\mathbf{L}+\mathbf{D})^{-1}\mathbf{U}, \mathbf{F} = (\mathbf{L} + \mathbf{D})^{-1}\mathbf{f}.$

Эти итерационные процессы называются методами Якоби и Зейделя . Представим их в компонентной записи. Метод Якоби будет иметь вид (перенесем итерационный индекс k вверх):

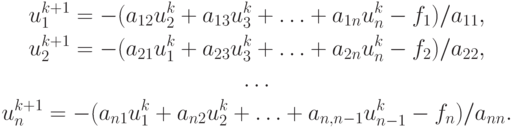
$\begin{gather*} u_1^{k + 1} = - (a_{12}u_2^k + a_{13}u_3^k + \ldots + a_{1n}u_n^k - f_1 )/a_{11}, \\ u_2^{k + 1} = - (a_{21}u_1^k + a_{23}u_3^k + \ldots + a_{2n}u_n^k - f_2 )/a_{22}, \\ \ldots \\ u_n^{k + 1} = - (a_{n1}u_1^k + a_{n2}u_2^k + \ldots + a_{n,n - 1}u_{n - 1}^k - f_n )/a_{nn}. \end{gather*}$

Метод Зейделя можно представить следующим образом:

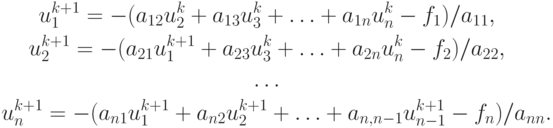
$\begin{gather*} u_1^{k + 1} = - (a_{12}u_2^k+ a_{13}u_3^k+ \ldots + a_{1n}u_n^k - f_1 )/a_{11}, \\ u_2^{k + 1} = - (a_{21}u_1^{k + 1}+ a_{23}u_3^k + \ldots + a_{2n}u_n^k - f_2 )/a_{22}, \\ \ldots \\ u_n^{k + 1} = - (a_{n1}u_1^{k + 1} + a_{n2}u_2^{k + 1} + \ldots + a_{n,n - 1}u_{n - 1}^{k + 1}- f_n )/a_{nn}. \end{gather*}$

Эти формулы легко выводятся, если учесть, что элементами матрицы D^-1 являются $d_{ii} = a_{ii}^{- 1}.$

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численное решение систем линейных алгебраических уравнений

2.5.2. Влияние ошибок округления на результат численного решения

2.5.3. Методы Якоби, Зейделя, верхней релаксации

Вопросы и ответы