Функции

Рекурсия

Определения функций не могут быть вложенными, т.е. нельзя внутри тела одной функции определить тело другой. Разумеется, можно вызвать одну функцию из другой. В том числе функция может вызвать сама себя.

Рассмотрим функцию вычисления факториала целого числа. Ее можно реализовать двумя способами. Первый способ использует итерацию:

int
fact(int n)
{
     int result = 1;
     for (int i = 1; i <= n; i++) 
          result = result * i;
     return result;
}

Второй способ:

int
fact(int n)
{
   if (n==0 || n==1)     // факториал 1 равен 1
          return 1;
   else            // факториал числа n равен
                   // факториалу n-1 
                   // умноженному на n  
                                                 
          return n * fact(n -1);
}

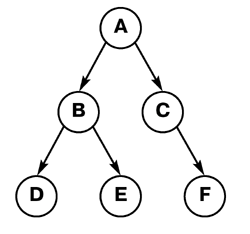
Функция   fact вызывает сама себя с модифицированными аргументами. Такой способ вычислений называется рекурсией. Рекурсия – это очень мощный метод вычислений. Значительная часть математических функций определяется в рекурсивных терминах. В программировании алгоритмы обработки сложных структур данных также часто бывают рекурсивными. Рассмотрим, например, структуру двоичного дерева. Дерево состоит из узлов и направленных связей. С каждым узлом могут быть связаны один или два узла, называемые сыновьями этого узла. Соответственно, для "сыновей" узел, из которого к ним идут связи, называется "отцом". Узел, у которого нет "отца", называется корнем. У дерева есть только один корень. Узлы, у которых нет "сыновей", называются листьями. Пример дерева приведен на рис. 5.1.

Рис. 5.1. Пример дерева.

В этом дереве узел A – корень дерева, узлы B и C – "сыновья" узла A, узлы D и E – "сыновья" узла B, узел F – "сын" узла C. Узлы D, E и F – листья. Узел B является корнем поддерева, состоящего из трех узлов B, D и E. Обход дерева (прохождение по всем его узлам) можно описать таким образом:

1. Посетить корень дерева.
2. Обойти поддеревья с корнями — "сыновьями" данного узла, если у узла есть "сыновья".
3. Если у узла нет "сыновей" — обход закончен.

Очевидно, что реализация такого алгоритма с помощью рекурсии не составляет труда.

Довольно часто рекурсия и итерация взаимозаменяемы (как в примере с факториалом). Выбор между ними может быть обусловлен разными факторами. Чаще рекурсия более наглядна и легче реализуется. Однако, в большинстве случаев итерация более эффективна.