|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Описание неопределенностей в теории принятия решений
Основные результаты в вероятностной модели. В классической вероятностной модели элементы исходной выборки 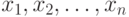 рассматриваются как независимые одинаково распределенные случайные величины. Как правило, существует некоторая константа C > 0 такая, что в смысле сходимости по вероятности
рассматриваются как независимые одинаково распределенные случайные величины. Как правило, существует некоторая константа C > 0 такая, что в смысле сходимости по вероятности
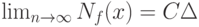 |
( 2) |
Соотношение (2) доказывается отдельно для каждой конкретной задачи.
При использовании классических статистических методов в большинстве случаев используемая статистика 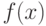 является асимптотически нормальной. Это означает, что существуют константы а и
является асимптотически нормальной. Это означает, что существуют константы а и  такие, что
такие, что
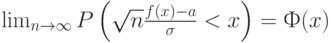
где 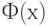 - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. При этом обычно оказывается, что
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. При этом обычно оказывается, что
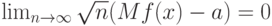
и
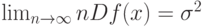
а потому в классической прикладной математической статистике средний квадрат ошибки статистической оценки равен
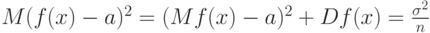
с точностью до членов более высокого порядка.
В статистике интервальных данных ситуация совсем иная - обычно можно доказать, что средний квадрат ошибки равен
 |
( 3) |
Из соотношения (3) можно сделать ряд важных следствий. Прежде всего, отметим, что правая часть этого равенства, в отличие от правой части соответствующего классического равенства, не стремится к 0 при безграничном возрастании объема выборки. Она остается больше некоторого положительного числа, а именно, квадрата нотны. Следовательно, статистика 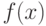 не является состоятельной оценкой параметра a. Более того, состоятельных оценок вообще не существует.
не является состоятельной оценкой параметра a. Более того, состоятельных оценок вообще не существует.
Пусть доверительным интервалом для параметра a, соответствующим заданной доверительной вероятности  , в классической математической статистике является интервал
, в классической математической статистике является интервал 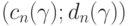 В статистике интервальных данных аналогичный доверительный интервал является более широким. Он имеет вид
В статистике интервальных данных аналогичный доверительный интервал является более широким. Он имеет вид 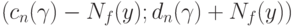 .Таким образом, его длина увеличивается на две нотны. Следовательно, при увеличении объема выборки длина доверительного интервала не может стать меньше, чем
.Таким образом, его длина увеличивается на две нотны. Следовательно, при увеличении объема выборки длина доверительного интервала не может стать меньше, чем 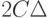 (см. формулу (2)).
(см. формулу (2)).
В статистике интервальных данных методы оценивания параметров имеют другие свойства по сравнению с классической математической статистикой. Так, при больших объемах выборок метод моментов может быть заметно лучше, чем метод максимального правдоподобия (т.е. иметь меньший средний квадрат ошибки - см. формулу (3)), в то время как в классической математической статистике второй из названных методов всегда не хуже первого. Именно так обстоит дело при оценивании параметров гамма-распределения.
Рациональный объем выборки. Анализ формулы (3) показывает, что в отличие от классической математической статистики нецелесообразно безгранично увеличивать объем выборки, поскольку средний квадрат ошибки остается всегда большим квадрата нотны. Поэтому представляется полезным ввести понятие "рационального объема выборки" 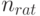 , при достижении которого продолжать наблюдения нецелесообразно.
, при достижении которого продолжать наблюдения нецелесообразно.
Как установить "рациональный объем выборки"? Можно воспользоваться идеей "принципа уравнивания погрешностей", выдвинутой в монографии [2]. Речь идет о том, что вклад погрешностей различной природы в общую погрешность должен быть примерно одинаков. Этот принцип дает возможность выбирать необходимую точность оценивания тех или иных характеристик в тех случаях, когда это зависит от исследователя. В статистике интервальных данных в соответствии с "принципом уравнивания погрешностей" предлагается определять рациональный объем выборки nrat из условия равенства двух слагаемых - метрологической составляющей, связанной с нотной, и статистической составляющей - в среднем квадрате ошибки (3), т.е. из условия
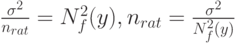
Для практического использования выражения для рационального объема выборки неизвестные теоретические характеристики необходимо заменить их оценками. Это делается в каждой конкретной задаче по-своему.
Исследовательскую программу в области статистики интервальных данных можно "в двух словах" сформулировать так: для любого алгоритма анализа данных (алгоритма прикладной статистики) необходимо вычислить нотну и рациональный объем выборки. Или иные величины из того же понятийного ряда, возникающие в многомерном случае, при наличии нескольких выборок и при иных обобщениях описываемой здесь простейшей схемы. Затем проследить влияние погрешностей исходных данных на точность оценивания, доверительные интервалы, значения статистик критериев при проверке гипотез, уровни значимости и другие характеристики статистических выводов. Очевидно, классическая математическая статистика является частью статистики интервальных данных, выделяемой условием 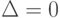 .
.
Нечеткие множества
Пусть  - некоторое множество. Подмножество
- некоторое множество. Подмножество  множества
множества  характеризуется своей характеристической функцией
характеризуется своей характеристической функцией
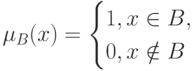 |
( 4) |
Что такое нечеткое множество? Обычно говорят, что нечеткое подмножество  множества
множества  характеризуется своей функцией принадлежности
характеризуется своей функцией принадлежности ![\mu_c \to[0,1]](/sites/default/files/tex_cache/766649e6b4c87e90eb63feb190ed6de3.png) Значение функции принадлежности в точке х показывает степень принадлежности этой точки нечеткому множеству. Нечеткое множество описывает неопределенность, соответствующую точке х - она одновременно и входит, и не входит в нечеткое множество
Значение функции принадлежности в точке х показывает степень принадлежности этой точки нечеткому множеству. Нечеткое множество описывает неопределенность, соответствующую точке х - она одновременно и входит, и не входит в нечеткое множество  . За вхождение -
. За вхождение -  шансов, за второе -
шансов, за второе - 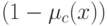 шансов.
шансов.
Если функция принадлежности  имеет вид (4) при некотором B, то
имеет вид (4) при некотором B, то  есть обычное (четкое) подмножество
есть обычное (четкое) подмножество  . Таким образом, теория нечетких множеств является не менее общей математической дисциплиной, чем обычная теория множеств, поскольку обычные множества - частный случай нечетких.
. Таким образом, теория нечетких множеств является не менее общей математической дисциплиной, чем обычная теория множеств, поскольку обычные множества - частный случай нечетких.
Соответственно можно ожидать, что теория нечеткости как целое обобщает классическую математику. Однако еще в 1970-х годах установлено, что теория нечеткости в определенном смысле сводится к теории случайных множеств и тем самым является частью классической математики. Другими словами, по степени общности обычная математика и нечеткая математика эквивалентны. Однако для практического применения в теории принятия решений описание и анализ неопределенностей с помощью теории нечетких множеств весьма плодотворны.
Обычное подмножество можно было бы отождествить с его характеристической функцией. Этого математики не делают, поскольку для задания функции (в ныне принятом подходе) необходимо сначала задать множество. Нечеткое же подмножество с формальной точки зрения можно отождествить с его функцией принадлежности. Однако термин "нечеткое подмножество" предпочтительнее при построении математических моделей реальных явлений.
