|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Доходность и риск
Безусловно, показатель доходности к погашению не является идеальным. Будучи средней эффективной процентной ставкой, он "заглаживает" возможные колебания доходности в течение периода владения облигацией. Кроме того, он совершенно не учитывает индивидуальные возможности реинвестирования доходов, которые имеются у отдельных инвесторов: эффективная ставка предполагает однократное реинвестирование в течение года. Тем не менее, пока еще не изобретено иного способа подсчета доходности, который в такой же степени чутко реагировал бы на любые изменения ожидаемого денежного потока. Поэтому именно YTM (и его разновидность YTC) получили наиболее широкое применение в финансовом анализе. Не следует забывать, что эти показатели являются ничем иным как разновидностями основополагающего финансового понятия – внутренней нормы доходности (IRR).
Наряду с купонными существуют облигации с нулевым купоном (бескупонные или дисконтные). Доход по ним образуется только за счет разницы между ценой покупки и продажи. Как правило, они продаются со скидкой (дисконтом) от номинальной цены, а выкупаются по номиналу. К этим инструментам вообще неприменимы понятия купонной и текущей доходности: их полная доходность включает в себя только вторую составляющую – прирост стоимости капитала. Методика расчета доходности краткосрочных дисконтных облигаций (например, ГКО) уже неоднократно рассматривалась в настоящем пособии, поэтому в данном параграфе будут рассмотрены только долгосрочные (с продолжительностью свыше 1 года) финансовые инструменты. Очевидно, что измерителем доходности таких инвестиций должна являться сложная процентная ставка. Рассмотрим пример: двухлетняя дисконтная облигация номиналом 10 тыс. рублей продается по курсу 78. Следовательно, общая сумма дохода к концу второго года по ней составит 2 тыс. 200 рублей (10000 – 7800). Доходность к погашению этой облигации может быть найдена из уравнения:
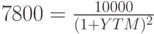
По сути дела, задача сводится к определению сложной эффективной годовой ставки по формуле (2.2.15). Применив эту формулу, получим  . Иными словами, разместив на банковский депозит 7800 рублей под эффективную ставку 13,228%, через 2 года с него можно было бы снять наращенную сумму 10 тыс. рублей
. Иными словами, разместив на банковский депозит 7800 рублей под эффективную ставку 13,228%, через 2 года с него можно было бы снять наращенную сумму 10 тыс. рублей 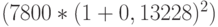 . Точно такой же результат можно получить, применив компьютерную функцию ВНДОХ для денежного потока (-7800, 0, 10000). Однако в данном случае задача проще, чем при расчете YTM купонных облигаций, поэтому нет необходимости для усложнения расчетов: достаточно помнить формулу определения эффективной ставки (2.2.15).
. Точно такой же результат можно получить, применив компьютерную функцию ВНДОХ для денежного потока (-7800, 0, 10000). Однако в данном случае задача проще, чем при расчете YTM купонных облигаций, поэтому нет необходимости для усложнения расчетов: достаточно помнить формулу определения эффективной ставки (2.2.15).
Ожидаемая доходность бессрочных облигаций, по которым выплачиваются "вечные" ренты, рассчитывается по формуле:
 |
( 5.3.3) |
 – сумма ежегодных купонных выплат;
– сумма ежегодных купонных выплат;
 – цена приобретения облигации.
– цена приобретения облигации.
Очевидно, что этот показатель отражает только текущую доходность, так как условиями размещения подобных займов не предусматривается выплата каких-то иных доходов. Тем не менее, никто не мешает инвестору запланировать перепродажу облигации через несколько лет владения ею по цене, которая может отличаться от цены покупки. В этом случае он сможет рассчитать доходность к погашению данного инструмента. Например, покупая за 46 фунтов стерлингов бессрочную консоль Казначейства Великобритании, по которой ежегодно выплачивается доход в сумме 4 фунта стерлингов, инвестор может рассчитывать на годовую доходность 8,696% (4 / 46). Однако, если по его "расчислению" через два года он сможет продать эту облигацию на вторичном рынке за 50 фунтов, то ее доходность к погашению (точнее, к перепродаже) должна находиться путем решения следу ющего уравнения:
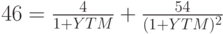
irr (а следовательно, и доходность к погашению облигации) данного денежного потока составит 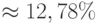 . Применив приближенную формулу расчета (5.2.3), получим:
. Применив приближенную формулу расчета (5.2.3), получим:

Основное отличие акций состоит в неопределенности величины ожидаемых по ним доходов. В этом смысле можно выделить привилегированные акции, дивиденды по которым, как правило, известны заранее и должны выплачиваться раньше дивидендов по обыкновенным акциям. По сути дела привилегированные акции являются промежуточной стадией между собственным (обыкновенные акции) и заемным (облигации) капиталом. Для определения их доходности используется формула, аналогичная применяемой для бессрочных облигаций:
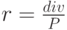 |
( 5.3.4) |
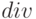 – сумма ожидаемых дивидендов на 1 акцию,
– сумма ожидаемых дивидендов на 1 акцию,
Точно так же, как для бессрочных облигаций, в случае планируемой перепродажи акции на вторичном рынке, полная доходность владения ею может быть определена как YTM.
Для обыкновенных акций прогнозирование величины будущих дивидендов является наиболее важной и самой сложной проблемой. Чаще всего при этом используется модель постоянного роста (модель Гордона), предполагающая неизменный в обозримом будущем темп прироста суммы дивидендов, выплачиваемых по акции. Ожидаемая доходность владения акцией в этом случае будет находиться по следующей формуле:
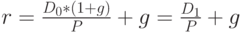 |
( 5.3.4) |
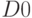 – последний выплаченный дивиденд по акции;
– последний выплаченный дивиденд по акции;
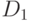 – дивиденд, ожидаемый к выплате в ближайшем периоде в будущем;
– дивиденд, ожидаемый к выплате в ближайшем периоде в будущем;
 – ожидаемый темп прироста дивиденда в будущем.
– ожидаемый темп прироста дивиденда в будущем.
Например, на рынке имеется предложение обыкновенных акций по цене 250 рублей за 1 шт. Известно, что в прошлом году по ним был выплачен дивиденд в сумме 30 рублей на 1 акцию. В дальнейшем ожидается непрерывный рост дивиденда на 2% в год. Ожидаемая доходность акции составит:
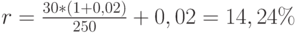
Абсолютно все формулы, рассмотренные в данном параграфе, строились на предположении об определенности потоков будущих доходов, выплачиваемых владельцам ценных бумаг. Однако в реальности 100%-й определенности практически никогда не существует. Даже самые надежные инструменты (например, правительственные облигации) несут в себе опасность того, что фактический результат может значительно отличаться от ожидаемого: высокая инфляция может "съесть" весь фиксированный доход по облигации, несмотря на четкое выполнение эмитентом своих номинальных обязательств. Следовательно, во всех финансовых расчетах должен присутствовать еще один важнейший параметр (о котором практически ничего не было сказано в предыдущих параграфах), характеризующий меру неопределенности, сопряженную с возможностью получения ожидаемого дохода. В финансах эта неопределенность обозначается термином риск, отражающим вероятность получения результата, отличающегося от запланированного. Так как важнейшим результатом любой финансовой операции является получение дохода на инвестиции, величина риска отождествляется со степенью разброса фактической доходности операции вокруг ее ожидаемой величины. Чем больше разброс данных, тем рискованнее финансовая операция.
Возвращаясь к рассмотренным выше формулам, можно сказать, что все полученные с их помощью результаты являются не более, чем субъективными оценками. Каждому результату должна быть приписана вероятность его возникновения в будущем. Большинство из них предполагает наличие вариантов, то есть множественность исходов. Поэтому от прогнозирования однозначных цифр необходимо перейти к изучению распределения вероятностей того или иного события. Без этого заучивание рассмотренных формул становится бессмысленным занятием, а попытки их практического применения обернутся существенным материальным ущербом для инвестора.
