Lecture
Распределение моментов поступления вызовов
Крутые распределения
Крутые распределения также называют гиперэкспоненциальными распределениями или обобщенными распределениями Эрланга с коэффициентом формы в интервале \[ 1 < \varepsilon \le 2 \] . Эта обобщенная функция распределения получена свертыванием k экспоненциальных распределений (рис.4.2). Здесь мы рассматриваем только случай, где все k экспоненциальных распределений идентичны. Тогда мы получаем следующую плотность функция, которая называется k распределением Эрланга (распределение Эрланга k -го порядка):
\[ f(t)=\frac{(\lambda t)^{k-1}}{(k-1)!}*\lambda * e^{-\lambda t}, \lambda > 0, t \ge 0, k=1,2,\dots. \] \[ F(t)=\sum_{j=k}^{\infty} \frac{(\lambda t)^j}{j!}*e^{-\lambda t} \] \[ =1-\sum_{j=0}^{k-1} \frac{(\lambda t)^j}{j!}*e^{-\lambda t} \]Следующие моменты могут быть найдены с использованием (3.31) и (3.32):
\[ m=\frac{k}{\lambda}, \] \[ \sigma^2=\frac{k}{\lambda^2}, \] \[ \varepsilon=1+\frac{\sigma^2}{m^2}=1+\frac 1k. \]i -тый нецентральный момент:
\[ m_i=\frac{(i+k-1)!}{(k-1)!}*\left (\frac{1}{\lambda}\right )^i. \]Функция плотности получена в секции 6.2.2. Средний остаток времени "жизни" \[ m_{1,r}(x) \] для \[ x \ge 0 \] будет меньше, чем средняя величина:
\[ m_{1,r}(x) \le m, x \ge 0. \]
Рис. 4.3. k распределения Эрланга со средней величиной. Случай k = 1 соответствует экспоненциальному распределению (функции плотности)
С этим распределением мы имеем два параметра \[ (\lambda, k) \] , доступные для наблюдений. Средняя величина часто сохраняется фиксированной. Чтобы изучить влияние параметра k в функции распределения, мы нормализуем все k распределения Эрланга к одной и той же самой средней величине как 1, распределение Эрланга, то есть экспоненциальное распределение заменим средним значением \[ 1/\lambda \] , a t -на k t или \[ \lambda \] на \[ \lambda k \] :
\[ f(t)dt=\frac{(\lambda kt)^{k-1}}{(k-1)!}e^{-\lambda kt} k \lambda dt, \] \[ m=\frac{1}{\lambda}, \] \[ \sigma^2=\frac{1}{k \lambda^2}, \] \[ \varepsilon=1+\frac 1k. \]Заметим, что коэффициент формы независим от времени. Функция (4.15) плотности проиллюстрирована на рис.4.3 для различных значений k с \[ \lambda =1 \] . Возьмем случай, когда k = 1 соответствует экспоненциальному распределению. Если \[ k \to m1 \] , мы получаем постоянный временной интервал ( \[ \varepsilon=1 \] ). Решая f(t) = 0, находим максимальное значение:
\[ \lambda t=\frac{k-1}{k} \]Так называемые крутые распределения носят такое имя, потому что увеличение функций распределения от 0 до 1 идет быстрее, чем в экспоненциальном распределении. В теории телетрафика мы иногда используем название - распределение Эрланга для усеченного Пуассоновского распределения (секция 7.3).
Плоские распределения
Общая функция распределения находится в этом случае с помощью взвешенной суммы экспоненциальных распределений (составное распределение) с коэффициентом формы \[ \varepsilon \ge 2 \] :
\[ F(t)=\int_0^{\infty}(1-e^{-\lambda t})dW(\lambda), \lambda > 0, t \ge 0, \]Функция веса может быть дискретна или непрерывна (интеграл Стилтьеса). Этот класс распределения соответствует параллельной комбинации экспоненциальных распределений (рис.4.4). Функция плотности называется полностью монотонной с чередующимися знаками (Пальма, 1957 [82]:
\[ (-1)^v*f^{(v)}(t) \ge 0. \]Среднее остаточное время "жизни" \[ т_{1,r} (х) \] для всего \[ х \ge 0 \] является большим, чем средняя величина:
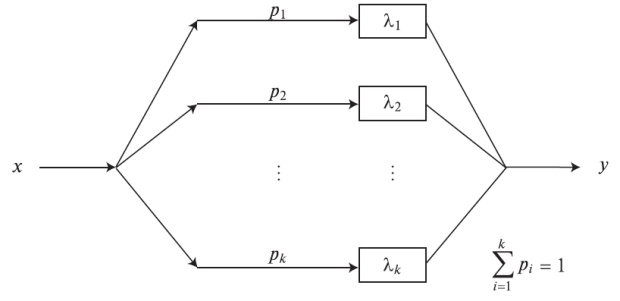
\[ m_{1,r}(x) \ge 0, x \ge 0. \]Комбинируя k экспоненциальных параллельных распределений и выбирая i - число ветви i с вероятностью \[ p_i \] , мы получаем гиперэкспоненциальное распределение, которое является плоским распределением ( \[ \varepsilon \ge 2 \] )
Гиперэкспоненциальное распределение
В этом случае \[ W(\lambda) \] - дискретно. Предположим, что нам даны следующие значения:
\[ \lambda_1, \lambda_2, \dots, \lambda_k, \]и что \[ W(\lambda) \] имеет положительные и увеличивающие значения:
\[ p_1, p_2, \dots, p_k, \]где
\[ \sum_{i=1}^k p_i=1. \]Для всех других значений \[ W(\lambda) \] является постоянным. В этом случае (4.20) становится:
\[ F(t)=1-\sum_{i=1}^k p_i*e^{-\lambda_it}, t \ge 0. \]Средние величины и коэффициент формы могут быть найдены из (3.36)и(3.37)( \[ \sigma_i=m_{1,i}=1/\lambda \] ):
\[ m_1=\sum_{i=1}^k \frac{p_i}{\lambda_i}, \] \[ \varepsilon=2\left \{ \sum_{i=1}^k \frac{p_i}{\lambda_i^2}\right \} \left / \left \{ \sum_{i=1}^k \frac{p_i}{\lambda_i} \right \}^2 \ge 2. \]Если k = 1 или все \[ \lambda_i \] равны, мы получаем экспоненциальное распределение.
Распределения этого класса называются гиперэкспоненциальными распределениями, и могут быть получены комбинацией k параллельных экспоненциальных распределений, где вероятность выбора i -того распределения - \[ p_i \] . Распределение называется плоским, потому что увеличения его функции распределения от 0 до 1 идет медленнее, чем при экспоненциальном распределении.
Практически, трудно оценить больше, чем один или два параметра. Самый важный случай - для \[ n=2(p_1=p, p_2=1-p) \]
\[ F(t)=1-p*e^{-\lambda_1 t}-(1-p)*e^{-\lambda_2 t}. \]Статистические проблемы возникают, даже когда мы имеем дело с тремя параметрами. Так, для практических приложений, мы обычно выбираем \[ \lambda_i=2\lambda *p_i \] . и, таким образом, уменьшаем число параметров до двух.
\[ F(t)=1-pe^{-2\lambda pt}-(1-p)e^{-2\lambda \lambda 1-p)t. \]Средняя величина и коэффициент формы получаются равными:
\[ m=\frac{1}{\lambda},\\ \varepsilon=\frac{1}{2p(1-p)}. \]При таком выборе параметров две ветви имеют тот же самый вклад в среднюю величину. Pис.4.5 иллюстрирует пример.
Распределения Кокса
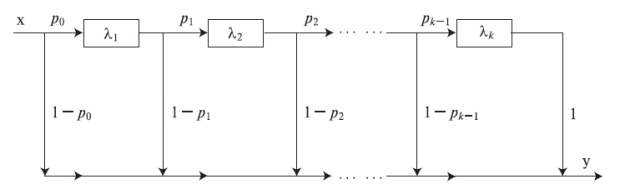
Комбинируя крутые и плоские распределения, мы получаем общий класс распределений (распределения фазового типа), которые может быть описаны с помощью экспоненциальной фазы в последовательном и параллельном случае (например, \[ k \times l \] матрицу). Чтобы проанализировать модель с таким видом распределений, мы можем применить теорию Марковских процессов, для которых имеются мощные инструментальные средства, такие, как метод диаграмм состояний (фазовый метод). В общем случае мы можем учесть обратную связь между состояниями (фазами).
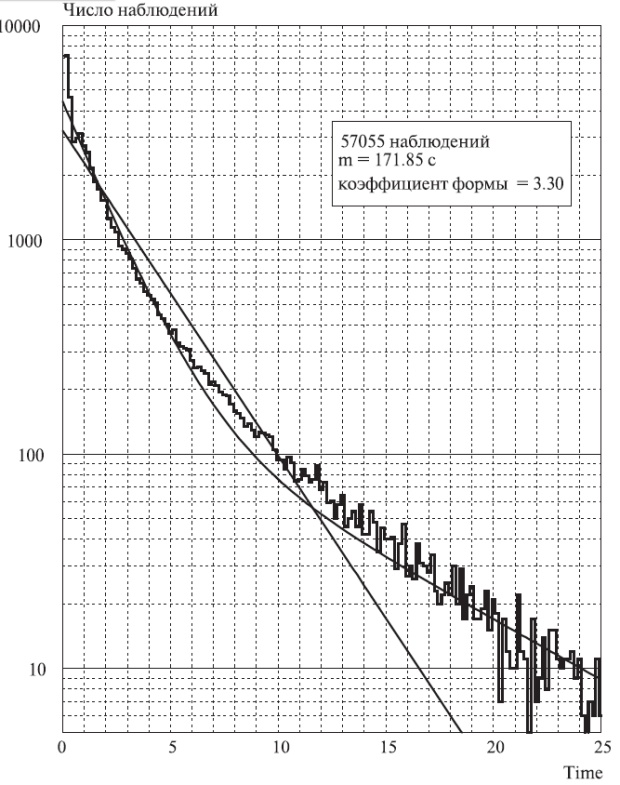
Рис. 4.5. Функция плотности (частотная) для времен пребывания в системе наблюдаемых линий на местной станции в течение часа наибольшей нагрузки.
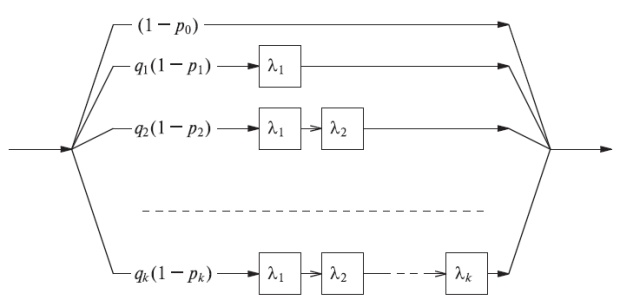
Рис. 4.6. Распределение Кокса - обобщенное распределение Эрланга, имеющее параллельные и последовательные экспоненциальные распределения.
Диаграмма состояния эквивалентна рис.4.7.
Рассмотрим распределение Кокса, которое показано на рис.4.6 (Кокс, 1955 [17]). Оно также иногда называется распределением эрланговского разветвления (иначе, распределением Эрланга с ветвями).
Средняя величина и дисперсия этого распределения Кокса (рис.4.7) получаются из формулы в секции 3.2 для последовательных и параллельных случайных переменных, как это показано на рис.4.6:
\[ m_1=\sum_{i=1}^k q_i(1-p_i) \left \{ \sum_{j=1}^i \frac{1}{\lambda_j} \right \}, \]где
\[ q_i=p_0*p_1* \dots p_{i-1}. \]Выражение \[ q_i(1-p_i) \] - вероятность перехода процесса, когда он находится в i -том состоянии. Средняя величина может быть выражена простой формулой:
\[ m_1=\sum_{i=1}^k \frac{q_i}{\lambda_i}=\sum_{i=1}^k m_{1,i}, \]где \[ m_{1,i}=\frac{q_i}{\lambda_i} \] - средняя величина в i -том состоянии. Второй момент получается
\[ m_2=\sum_{i=1}^k\{q_i(1-p_i)*m_{2,i}\},\\ \quad=\sum_{i=1}^k\left\{ q_i(1-p_i)*\left \{\sum_{j=1}^i \frac{1}{\lambda_j^2}+\left ( \sum_{j=1}^i \frac{1}{\lambda_j}\right)^2 \right\} \right\}, \]где \[ m_{2,i} \] получен из (3.8): \[ m_{2,i}=\sigma_{2,i}^2+m_{1,i}^2 \] .; это можно записать как:
\[ m_2=2*\sum_{i=1}^k \left\{ \left(\sum_{j=1}^i \frac{1}{\lambda_j}\right)*\frac{q_i}{\lambda_i} \right \}. \]После чего получаем дисперсию (3.8):
\[ \sigma^2=m_2-m_1^2. \]Сложение двух распределений Кокса для случайных переменных дает другое распределение Кокса для случайной переменной, то есть этот класс является замкнутым по отношению к сложению.
Функция распределения Кокса может быть записана как сумма экспоненциальных функций:
\[ 1-F(t)=\sum_{i=1}^k c_i*e^{-\lambda_i t}. \]где
\[ 0 \le \sum_{i=1}^k c_i \le 1, \]и
\[ - \infty < c_i < +\infty. \]Мультиноминальное распределение
Для более поздних приложений важны следующие свойства. Если мы полагаем, что точка выбрана наугад в пределах временного интервала, подчиняющегося распределению Кокса, то вероятность, что эта точка - в пределах фазы i, равна:
\[ \frac{m_i}{m}, i=1,2,\dots, k. \]Если мы повторяем этот эксперимент \[ y \] раз (независимо), то вероятность, что фаза \[ i \] наступала \[ y_i \] раз, определяется с помощью мулътиноми-нальногораспределения (оно же - полиномиальное распределение):
\[ p\{y|y_1, y_2, \dots, y_k\}=\begin{pmatrix} y\\ y_1y_2 \dots y_k \end{pmatrix}*\left (\frac{m_{1,1}}{m}\right )^{y_1}*\left (\frac{m_{1,2}}{m} \right)^{y_2} \dots \left(\frac{m_{1,k}}{m} \right)^{y_k}. \]где
\[ y=\sum_{i=1}^k y_i, \]и
\[ \begin{pmatrix} y\\ y_1y_2 \dots y_k \end{pmatrix}=\frac{y!}{y_1!* y_2! \dots y_k!}. \]Элементы в (4.38) называются мультиноминальными коэффициентами. Благодаря свойству экспоненциальных распределений - отсутствию памяти, - мы имеем полную информацию об остаточном времени "жизни", если знаем номер текущей фазы.