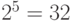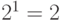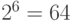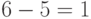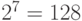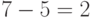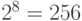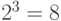Импульсно-кодовое преобразование
Алгоритм компандирования по A-закону
Процесс компандирования при современных параметрах микросхем может осуществляться с помощью постоянных запоминающих устройств прямым табличным преобразованием. Однако существуют алгоритмы, позволяющие делать другое преобразование путем несложного пересчета.
Алгоритм определения составляющих формата компандирования по рис. 8.6 для числа  иллюстрируется таблицей 8.3 и выполняется в следующем порядке.
иллюстрируется таблицей 8.3 и выполняется в следующем порядке.
В таблице показана линейная комбинация, содержащая старшие разряды величины отсчета. 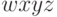 указывает номер шага квантования, прочерки указывают на те разряды, которые могут быть пропущены в связи с уменьшением точности для данной величины отсчета.
указывает номер шага квантования, прочерки указывают на те разряды, которые могут быть пропущены в связи с уменьшением точности для данной величины отсчета.
- Знак определяется согласно знаку заданного числа N и кодируется следующим образом:
0 — положительная величина отсчета,
1 — отрицательная величина.
- Номер сегмента
Находится такое минимальное из возможных число
 , что
, что 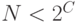
(точнее,
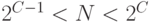 ).
).Номер сегмента определяется как
 .
. - Номер шага
Номер шага квантования может быть определен несколькими способами.
1-й способ. После определения номера сегмента вычисляется следующая разность:
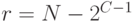 .
.Эта разность переводится в двоичную форму, содержащую
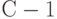 разряд, и в конце двоичной комбинации удаляются
разряд, и в конце двоичной комбинации удаляются  младших разрядов. Что дает
младших разрядов. Что дает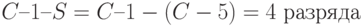 .
.2-й способ. Определяются разряды номера шага, а именно
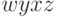 .
. определяется следующим образом.
определяется следующим образом.
a. Сравниваются числа  и
и 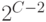 .
.
Если 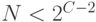 , то
, то  . Устанавливается новое число
. Устанавливается новое число  и выполняется шаг
и выполняется шаг  этого алгоритма, в другом случае (
этого алгоритма, в другом случае (  )
) 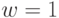 , вычисляется
, вычисляется 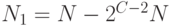 и выполняется пункт
и выполняется пункт  этого алгоритма.
этого алгоритма.
Далее сравниваются числа  и
и 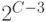 .
.
Если 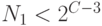 , то
, то  . Устанавливается новое число
. Устанавливается новое число 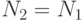 и выполняется следующий шаг этого алгоритма, в другом случае (
и выполняется следующий шаг этого алгоритма, в другом случае ( 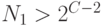 )
) 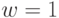 и вычисляется
и вычисляется 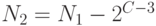 и выполняется следующий шаг этого алгоритма.
и выполняется следующий шаг этого алгоритма.
Далее аналогичная процедура выполняется на следующих шагах для  и
и  .
.
Рассмотрим несколько примеров компандирования отсчетов.
Предположим, нам надо получить все характеристики значения отсчета 68.
Минимальное число, удовлетворяющее условию:
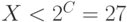
это 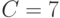 .
.
Тогда десятичный номер сегмента равен  (или двоичное значение 010). Далее вычисляем остаток:
(или двоичное значение 010). Далее вычисляем остаток:
 .
.
Вычислим номер разряда первым способом. Двоичное значение для 6
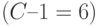 оставшихся разрядов равно 000011, поскольку
оставшихся разрядов равно 000011, поскольку 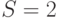 . Исключаем два последних разряда в двоичном представлении, получаем код шага квантования
. Исключаем два последних разряда в двоичном представлении, получаем код шага квантования  . Полный восьмиразрядный формат равен 0 010 0000.
. Полный восьмиразрядный формат равен 0 010 0000.
Вычислим номер разряда вторым способом.
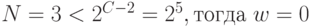
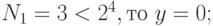
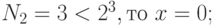
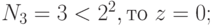
 .
.
Рассмотрим число 125.
Из неравенства 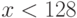 получаем
получаем 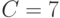 .
.
Номер сегмента 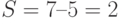 .
.
Остаток 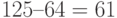 .
.
Первый способ.
Двоичное представление остатка 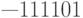 . Исключая последние два знака, получаем код шага квантования
. Исключая последние два знака, получаем код шага квантования 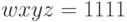 .
.
Второй способ.
 .
.
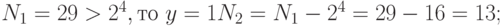

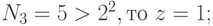
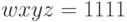 .
.