НОУ ИНТУИТ | Основы программирования. Лекция 2: Типы переменных. Целые и вещественные переменные, представление целых и вещественных чисел в компьютере

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 16.09.2005 | Уровень: для всех | Доступ: свободно | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 205 студентам

| Поделиться |

Поддержать программу

Вещественные переменные

Вещественные числа представляются в компьютере в так называемой экспоненциальной, или плавающей, форме. Вещественное число r имеет вид

$r = \pm 2^{e} \cdot m$

Представление числа состоит из трех элементов:

знак числа - плюс или минус. Под знак числа отводится один бит в двоичном представлении, он располагается в старшем, т.е. знаковом разряде. Единица соответствует знаку минус, т.е. отрицательному числу, ноль - знаку плюс. У нуля знаковый разряд также нулевой;
показатель степени e, его называют порядком или экспонентой. Экспонента указывает степень двойки, на которую домножается число. Экспонента может быть как положительной, так и отрицательной (для чисел, меньших единицы). Под экспоненту отводится фиксированное число двоичных разрядов, обычно восемь или одиннадцать, расположенных в старшей части двоичного представления числа, сразу вслед за знаковым разрядом;
мантисса m представляет собой фиксированное количество разрядов двоичной записи вещественного числа в диапазоне от 1 до 2:
```
1 <= m<2
```
Следует подчеркнуть, что левое неравенство нестрогое - мантисса может равняться единице, а правое - строгое, мантисса всегда меньше двух. Разряды мантиссы включают один разряд целой части, который ввиду приведенного неравенства всегда равен единице, и фиксированное количество разрядов дробной части. Поскольку старший двоичный разряд мантиссы всегда равен единице, хранить его необязательно, и в двоичном коде он отсутствует. Фактически двоичный код хранит только разряды дробной части мантиссы.

В языке Си вещественным числам соответствуют типы float и double. Элемент типа float занимает 4 байта, в которых один бит отводится под знак, восемь - под порядок, остальные 23 - под мантиссу (на самом деле, в мантиссе 24 разряда, но старший разряд всегда равен единице, поэтому хранить его не нужно). Тип double занимает 8 байтов, в них один разряд отводится под знак, 11 - под порядок, остальные 52 - под мантиссу. На самом деле в мантиссе 53 разряда, но старший всегда равен единице и поэтому не хранится. Поскольку порядок может быть положительным и отрицательным, в двоичном коде он хранится в смещенном виде: к нему прибавляется константа, равная абсолютной величине максимального по модулю отрицательного порядка. В случае типа float она равна 127, в случае double - 1023.

Основным типом является тип double, именно он наиболее естественен для компьютера. В программировании следует по возможности избегать типа float, так как его точность недостаточна, а процессор все равно при выполнении операций преобразует его в тип double. (Один из немногих случаев, где применение типа float оправдано, - трехмерная компьютерная графика.)

Несколько примеров представления вещественных чисел в плавающей форме:

1.0 = +2⁰*1.0
Здесь порядок равен 0, мантисса - 1. В двоичном коде мантисса состоит из одних нулей, так как старший разряд мантиссы (всегда единичный) в коде отсутствует. Порядок хранится в двоичном коде в смещенном виде, он равен 127 в случае float и 1023 в случае double ;
3.5 = +2¹*1.75
Порядок равен единице, мантисса состоит из трех единиц, из которых в двоичном коде хранятся две: 1100...0 ; смещенный порядок равен 128 для float и 1024 для double ;
0.625 = +2^-1*1.25
Порядок отрицательный и равен -1, дробная часть мантиссы равна 0100...0 ; смещенный порядок равен 126 для float и 1022 для double ;
100.0 = +2⁶*1.5625
Порядок равен шести, дробная часть мантиссы равна 100100...0 ; смещенный порядок равен 133 для float и 1029 для double.

При выполнении сложения двух положительных плавающих чисел происходят следующие действия:

выравнивание порядков. Определяется число с меньшим порядком. Затем последовательно его порядок увеличивается на единицу, а мантисса делится на 2, пока порядки двух чисел не сравняются. Аппаратно деление на 2 соответствует сдвигу двоичного кода мантиссы вправо, так что эта операция выполняется быстро. При сдвигах правые разряды теряются, из-за этого может произойти потеря точности (в случае, когда правые разряды ненулевые);
сложение мантисс;
нормализация: если мантисса результата стала равна или превысила двойку, то порядок увеличивается на единицу, а мантисса делится на 2. В результате этого мантисса попадает в интервал 1 <= m<2. При этом возможна потеря точности, а также переполнение, когда порядок превышает максимально возможную величину.

Вычитание производится аналогичным образом. При умножении порядки складываются, а мантиссы перемножаются как целые числа, после чего у результата правые разряды отбрасываются.

Машинный эпсилон

Действия с плавающими числами из-за ошибок округления лишь приближенно отражают арифметику настоящих вещественных чисел. Так, если к большому плавающему числу прибавить очень маленькое, то оно не изменится. Действительно, при выравнивании порядков все значащие биты мантиссы меньшего числа могут выйти за пределы разрядной сетки, в результате чего оно станет равным нулю. Таким образом, с плавающими числами возможна ситуация, когда

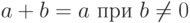
$a+b = a \ при \ b \ne 0$

Более того, для сложения не выполняется закон ассоциативности:

$a+(b+c) \ne (a+b)+c$

Действительно, пусть $\varepsilon$ - максимальное плавающее число среди чисел, удовлетворяющих условию

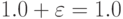
$1.0+\varepsilon = 1.0$

(приведенные выше рассуждения показывают, что такие числа существуют). Тогда

$(1.0+\varepsilon )+\varepsilon \ne 1.0+(\varepsilon +\varepsilon )$

поскольку левая часть неравенства равна единице, а правая строго больше единицы (это следует из максимальности числа $\varepsilon$ ).

Число $\varepsilon$ часто называют машинным эпсилоном или, чуть менее корректно, машинным нулем, поскольку при прибавлении к единице оно ведет себя как ноль. Величина машинного эпсилона характеризует точность операций компьютера. Она примерно одинакова для всех современных компьютеров: большинство процессоров работают с восьмибайтовыми плавающими числами (тип double в Си), а арифметика плавающих чисел подчиняется строгим международным стандартам.

Оценим величину машинного эпсилона для типа double. Число 1.0 записывается в плавающей форме как

1.0 = +2⁰*1.0.

Порядок плавающего числа 1.0 равен нулю. При сложении 1.0 с числом $\varepsilon$ производится выравнивание порядка путем многократного сдвига мантиссы числа $\varepsilon$ вправо и увеличения его порядка на 1. Поскольку все разряды числа $\varepsilon$ должны в результате выйти за пределы разрядной сетки, должно быть выполнено 53 сдвига. Порядок числа $\varepsilon$ после этого должен стать равным порядку числа 1.0, т.е. нулю. Следовательно, изначально порядок числа $\varepsilon$ должен быть равным -53:

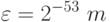
$\varepsilon = 2^{-53} \ m$

где m - число в диапазоне от единицы до двух. Таким образом, величина машинного эпсилона составляет примерно

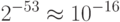
$2^{-53} \approx 10^{-16}$

Приблизительно точность вычислений составляет 16 десятичных цифр. (Это также можно оценить следующим образом: 53 двоичных разряда составляют примерно 15.95 десятичных, поскольку 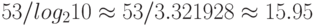$53/log_{2}10 \approx 53/3.321928 \approx 15.95$ .)

В случае четырехбайтовых плавающих чисел (тип float языка Си) точность вычислений составляет примерно 7 десятичных цифр. Это очень мало, поэтому тип float чрезвычайно редко применяется на практике. К тому же процессор сконструирован для работы с восьмибайтовыми вещественными числами, а при работе с четырехбайтовыми он все равно сначала приводит их к восьмибайтовому типу. В программировании следует избегать типа float и всегда пользоваться типом double.

Некоторые процессоры применяют внутреннее представление плавающих чисел с большим количеством разрядов мантиссы. Например, процессор Intel использует 80-битовое (десятибайтовое) представление. Поэтому точность вычислений, которые не записывают промежуточные результаты в память, может быть несколько выше указанных оценок.

Кроме потери точности, при операциях с вещественными числами могут происходить и другие неприятности:

переполнение - когда порядок результата больше максимально возможного значения. Эта ошибка часто возникает при умножении больших чисел;
исчезновение порядка - когда порядок результата отрицательный и слишком большой по абсолютной величине, т.е. порядок меньше минимально допустимого значения. Эта ошибка может возникнуть при делении маленького числа на очень большое или при умножении двух очень маленьких по абсолютной величине чисел.

Кроме того, некорректной операцией является деление на ноль. В отличие от операций с целыми числами, переполнение и исчезновение порядка считаются ошибочными ситуациями и приводят к аппаратному прерыванию работы процессора. Программист может задать реакцию на прерывание - либо аварийное завершение программы, либо, например, при переполнении присваивать результату специальное значение плюс или минус бесконечность, а при исчезновении порядка - ноль. Заметим, что среди двоичных кодов, представляющих плавающие числа, имеется несколько специальных значений. Перечислим некоторые из них:

бесконечно большое число - это плавающее число с очень большим положительным порядком и, таким образом, очень большое по абсолютной величине. Оно может иметь знак плюс или минус;
бесконечно малое, или денормализованное, число - это ненулевое плавающее число с очень большим отрицательным порядком (т.е. очень маленькое по абсолютной величине);
Not a Number, или NaN - двоичный код, который не является корректным представлением какого-либо вещественного числа.

Любые операции с константой NaN приводят к прерыванию, поэтому она удобна при отладке программы - ею перед началом работы программы инициализируются значения всех вещественных переменных. Если в результате ошибки программиста при вычислении выражения используется переменная, которой не было присвоено никакого значения, то происходит прерывание из-за операции со значением NaN и ошибка быстро отслеживается. К сожалению, в случае целых чисел такой константы нет: любой двоичный код представляет некоторое целое число.

Запись вещественных констант

Вещественные константы записываются в двух формах - с фиксированной десятичной точкой или в экспоненциальном виде. В первом случае точка используется для разделения целой и дробной частей константы. Как целая, так и дробная части могут отсутствовать. Примеры:

1.2,   0.725,   1.,   .35,   0.

В трех последних случаях отсутствует либо дробная, либо целая часть. Десятичная точка должна обязательно присутствовать, иначе константа считается целой. Отметим, что в программировании именно точка, а не запятая, используется для отделения дробной части; запятая обычно служит для разделения элементов списка.

Экспоненциальная форма записи вещественной константы содержит знак, мантиссу и десятичный порядок (экспоненту). Мантисса - это любая положительная вещественная константа в форме с фиксированной точкой или целая константа. Порядок указывает степень числа 10, на которую домножается мантисса. Порядок отделяется от мантиссы буквой "e" (от слова exponent), она может быть прописной или строчной. Порядок может иметь знак плюс или минус, в случае положительного порядка знак плюс можно опускать. Примеры:

1.5e+6      константа эквивалентна  1500000.0
1e-4        константа эквивалентна  0.0001
-.75E3      константа эквивалентна  -750.0

Дальше >>

Авторизоваться

Основы программирования

Типы переменных. Целые и вещественные переменные, представление целых и вещественных чисел в компьютере

Вещественные переменные

Машинный эпсилон

Запись вещественных констант

Вопросы и ответы