О деревьях
Представление с помощью списка ребер и кода Прюфера
Дерево при этом способе задается перечислением пар 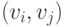 или
троек
или
троек 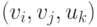 , если дополнительно нужна нумерация
ребер. Характер связей в списке определяется исходя из условий задачи.
, если дополнительно нужна нумерация
ребер. Характер связей в списке определяется исходя из условий задачи.
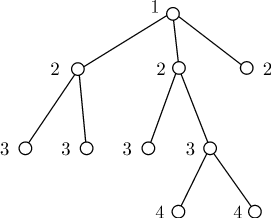
Для дерева, изображенного на (рис.11.1), имеем:
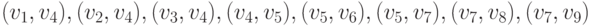 .
.
Алгоритм построения кода Прюфера
Пусть  — дерево с множеством вершин
— дерево с множеством вершин 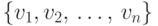 .
Будем считать, что номер вершины
.
Будем считать, что номер вершины 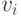 равен
равен  .
Сопоставим дереву
.
Сопоставим дереву  последовательность
последовательность 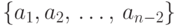 по следующему
правилу, представленному в виде функции: Функция кода Прюфера (
по следующему
правилу, представленному в виде функции: Функция кода Прюфера (  : дерево)
: дерево) 
- Пусть
 обозначает число вершин в
обозначает число вершин в  ,
а
,
а  — целочисленный вектор
длины
— целочисленный вектор
длины  ;
; -
![B=[1:n]](/sites/default/files/tex_cache/eec35446cb54743f0aa2d012299cc78e.png) ;
; - Для
 от
от  до
до  цикл
цикл -
 ;
; -
![a[i]](/sites/default/files/tex_cache/595711c58954cfc2eb727cba561e3512.png) — номер вершины, с которой смежна вершина с
номером
— номер вершины, с которой смежна вершина с
номером  ;
; -
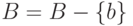 ;
; - удалить из
 вершины с номером
вершины с номером  ;
; - возврат
 .
.
Пример. Для дерева  . код Прюфера имеет вид
. код Прюфера имеет вид ![P_{2}
(T)= [2,5,5,5,6,6,10,9,10,11,13,15,15,10,13,13,13]](/sites/default/files/tex_cache/dac253cd827eda1d4cb055c1280467e1.png) .
.
В случае корневого ордерева процедура получения кода Прюфера аналогична.
Необходимо только на последнем месте указывать корневую вершину и при
распаковке кода исключать номер этой вершины из множества  .
.
Алгоритм раскодирования
Распаковка кода Прюфера осуществляется следующей функцией:
Функция
распаковки (  : код)
: код) 
- Пусть
 состоит из вершин
состоит из вершин 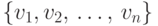 , таких, что номер
вершины
, таких, что номер
вершины 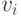 равен
равен  , где
, где  —
длина кода
—
длина кода  плюс 2;
плюс 2; -
![B=[1: n]](/sites/default/files/tex_cache/1c75e42e09a6f9e5923cf62a82a078a0.png) ;
; - Для
 от
от  до
до  цикл;
цикл; -
![b=\min \{ k\in B.k\ne A[j]](/sites/default/files/tex_cache/d68f6581e5b15b0e75f493bc7af6fe7b.png) для любого
для любого 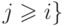 ;
; - В
 добавить ребро, соединяющее вершины с номерами
добавить ребро, соединяющее вершины с номерами  и
и ![A[i]](/sites/default/files/tex_cache/8a6b5ab46e06fa60418f7c34e624b076.png) ;
; -
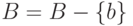 ;
; - возврат
 .
.
Уровневые коды корневых деревьев
Пусть 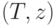 обозначает корневое дерево с лежащим в его основе
свободным деревом
обозначает корневое дерево с лежащим в его основе
свободным деревом  и корнем
и корнем  . Уровень
вершины
. Уровень
вершины  в
в 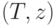 — это
расстояние от
— это
расстояние от  до
до  плюс единица. Уровневый код
(обозначение
плюс единица. Уровневый код
(обозначение ![L(T,z)=[l_{1},l_{2} \dts l_{n}]](/sites/default/files/tex_cache/79643f8077e7c4a7d0a85217ca5766a8.png) ) — это последовательность
целых чисел, полученная выписыванием уровней вершин дерева
) — это последовательность
целых чисел, полученная выписыванием уровней вершин дерева 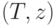 в постфиксном порядке.
в постфиксном порядке.
Уровневый
код называется каноническим
(обозначается 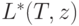 ), если он является наибольшим в
лексикографическом упорядочении среди всех уровневых кодов, описывающих
дерево.
), если он является наибольшим в
лексикографическом упорядочении среди всех уровневых кодов, описывающих
дерево.
Пример. Для дерева  , изображенного на (рис.11. 1), имеем
, изображенного на (рис.11. 1), имеем ![L(T,z)=[3,3,2,4,4,3,2,2,1]](/sites/default/files/tex_cache/c0ae5ac5f70a4031f1fa62abf612bd6d.png) — обычный уровневый код, а
канонический уровневый код
— обычный уровневый код, а
канонический уровневый код ![L^{*}(T,z)) =[4,4,3,3,2,3,3,2,2,1]](/sites/default/files/tex_cache/d3a1ea257bda360cafd80f012b3dd409.png) .
.