Индуктивные функции на пространстве последовательностей
Задачи для самостоятельного решения
При решении задач, приведенных ниже, необходимо выяснить, является
ли индуктивной заданная функция  . В случае ее индуктивности
следует предъявить отображение
. В случае ее индуктивности
следует предъявить отображение  , иначе нужно построить
индуктивное
расширение
, иначе нужно построить
индуктивное
расширение  исходной функции и предъявить
исходной функции и предъявить  для
него. В последнем
случае нужно также указать отображение
для
него. В последнем
случае нужно также указать отображение  и исследовать
построенное
расширение на минимальность (минимальность не является обязательным
условием). Завершить решение следует написанием
программы, реализующей однопроходный алгоритм, с указанием соответствия
между программными переменными и
обозначениями, использованными в теоретической части решения. Необходимо
объяснить, как в программе реализуется вычисление
и исследовать
построенное
расширение на минимальность (минимальность не является обязательным
условием). Завершить решение следует написанием
программы, реализующей однопроходный алгоритм, с указанием соответствия
между программными переменными и
обозначениями, использованными в теоретической части решения. Необходимо
объяснить, как в программе реализуется вычисление  или
или  на пустой
(или ее заменяющей) цепочке, как именно реализовано перевычисление
функции при удлинении цепочки и как находится
на пустой
(или ее заменяющей) цепочке, как именно реализовано перевычисление
функции при удлинении цепочки и как находится  в
случае использования индуктивного расширения.
в
случае использования индуктивного расширения.
Задача 9.5. Напишите программу, определяющую количество минимальных элементов в последовательности неположительных целых чисел.
Указание В данном случае для доопределения индуктивного расширения на пустой цепочке нет необходимости использовать величины Integer.MIN_VALUE или Integer.MAX_VALUE.
Задача 9.6. Напишите программу, определяющую значение в целой точке  многочлена,
заданного последовательностью его целых коэффициентов (в порядке
возрастания степеней).
многочлена,
заданного последовательностью его целых коэффициентов (в порядке
возрастания степеней).
Задача 9.7. Напишите программу, определяющую значение в целой точке  производной многочлена,
заданного последовательностью его целых коэффициентов (в порядке
убывания степеней).
производной многочлена,
заданного последовательностью его целых коэффициентов (в порядке
убывания степеней).
Указание
Продифференцировав по  равенство
равенство  и подставив затем
и подставив затем  , получите
соотношения
, получите
соотношения  и
и  , которые помогут построить
индуктивное расширение исходной функции.
, которые помогут построить
индуктивное расширение исходной функции.
Задача 9.8. Напишите программу, определяющую правильность формулы над
алфавитом из четырех символов 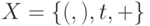 . Формула считается правильной,
если она может быть получена с помощью следующей НФБН:
. Формула считается правильной,
если она может быть получена с помощью следующей НФБН:  .
.
Указание
Рассмотрите следующее индуктивное расширение  функции
функции  , где
, где  ,
,  ,
, 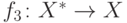 , определены следующим образом:
, определены следующим образом:
 может быть продолжена до правильной формулы,
может быть продолжена до правильной формулы,
 = разность числа левых и правых скобок в
= разность числа левых и правых скобок в  ,
,
 последний элемент
последний элемент  .
.
Задача 9.9. Напишите программу, определяющую номер  последнего элемента, равного
последнего элемента, равного  ,
в последовательности целых чисел. В том случае, если число
,
в последовательности целых чисел. В том случае, если число  в
последовательности не встречается, положите
в
последовательности не встречается, положите 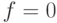 .
.
