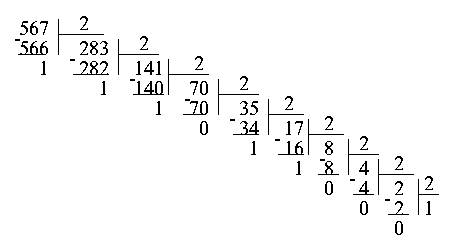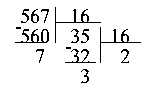Основы информатики
Двоичная система счисления
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам. Но, не всегда и не везде люди пользовались десятичной системой счисления. В Китае, например, долгое время применялась пятеричная система счисления. В ЭВМ используют двоичную систему потому, что она имеет ряд преимуществ перед другими:
- для ее реализации используются технические элементы с двумя возможными состояниями (есть ток - нет тока, намагничен - ненамагничен);
- представление информации посредством только двух состояний надежно и помехоустойчиво ;
- возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
- двоичная арифметика проще десятичной (двоичные таблицы сложения и умножения предельно просты).
В двоичной системе счисления всего две цифры, называемые двоичными (binary digits). Сокращение этого наименования привело к появлению термина бит, ставшего названием разряда двоичного числа. Веса разрядов в двоичной системе изменяются по степеням двойки. Поскольку вес каждого разряда умножается либо на 0, либо на 1, то в результате значение числа определяется как сумма соответствующих значений степеней двойки. Если какой-либо разряд двоичного числа равен 1, то он называется значащим разрядом. Запись числа в двоичном виде намного длиннее записи в десятичной системе счисления.
Арифметические действия, выполняемые в двоичной системе, подчиняются тем же правилам, что и в десятичной системе. Только в двоичной системе перенос единиц в старший разряд возникает чаще, чем в десятичной. Вот как выглядит таблица сложения в двоичной системе:
Таблица умножения для двоичных чисел еще проще:
Рассмотрим подробнее, как происходит процесс умножения двоичных чисел. Пусть надо умножить число 1101 на 101 (оба числа в двоичной системе счисления). Машина делает это следующим образом: она берет число 1101 и, если первый элемент второго множителя равен 1, то она заносит его в сумму. Затем сдвигает число 1101 влево на одну позицию, получая тем самым 11010, и если, второй элемент второго множителя равен единице, то тоже заносит его в сумму. Если элемент второго множителя равен нулю, то сумма не изменяется.
Двоичное деление основано на методе, знакомом вам по десятичному делению, т. е. сводится к выполнению операций умножения и вычитания. Выполнение основной процедуры - выбор числа, кратного делителю и предназначенного для уменьшения делимого, здесь проще, так как таким числом могут быть только либо 0, либо сам делитель.
Следует отметить, что большинство калькуляторов, реализованных на ЭВМ (в том числе и KCalc) позволяют осуществлять работу в системах счисления с основаниями 2, 8, 16 и, конечно, 10.
8-ная и 16-ная системы счисления
При наладке аппаратных средств ЭВМ или создании новой программы возникает необходимость "заглянуть внутрь" памяти машины, чтобы оценить ее текущее состояние. Но там все заполнено длинными последовательностями нулей и единиц двоичных чисел. Эти последовательности очень неудобны для восприятия человеком, привыкшим к более короткой записи десятичных чисел. Кроме того, естественные возможности человеческого мышления не позволяют оценить быстро и точно величину числа, представленного, например, комбинацией из 16 нулей и единиц.
Для облегчения восприятия двоичного числа решили разбивать его на группы разрядов, например, по три или четыре разряда. Эта идея оказалась очень удачной, так как последовательность из трех бит имеет 8 комбинаций, а последовательность из 4 бит - 16. Числа 8 и 16 являются степенями двойки, поэтому легко находить соответствие с двоичными числами. Развивая эту идею, пришли к выводу, что группы разрядов можно закодировать, сократив при этом длину последовательности знаков. Для кодировки трех битов требуется восемь цифр, поэтому взяли цифры от 0 до 7 десятичной системы. Для кодировки же четырех битов необходимо шестнадцать знаков; для этого взяли 10 цифр десятичной системы и 6 букв латинского алфавита: A, B, C, D, E, F. Полученные системы, имеющие основания 8 и 16, назвали соответственно восьмеричной и шестнадцатеричной.
В восьмеричной (octal) системе счисления используются восемь различных цифр 0, 1, 2, 3, 4, 5, 6, 7. Основание системы - 8. При записи отрицательных чисел перед последовательностью цифр ставят знак минус. Сложение, вычитание, умножение и деление чисел, представленных в восьмеричной системе, выполняются весьма просто подобно тому, как это делают в общеизвестной десятичной системе счисления.
В шестнадцатеричной (hexadecimal) системе счисления применяется десять различных цифр и шесть первых букв латинского алфавита. При записи отрицательных чисел слева от последовательности цифр ставят знак минус. Для того чтобы при написании компьютерных программ отличить числа, записанные в шестнадцатеричной системе, от других, перед числом ставят 0x. То есть 0x11 и 11 - это разные числа. В других случаях можно указать основание системы счисления нижним индексом.
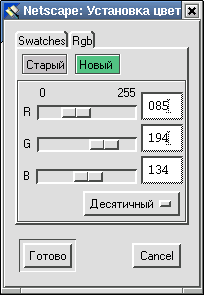
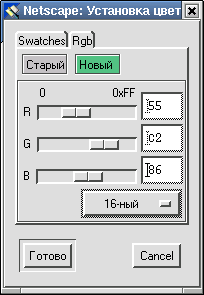
Шестнадцатеричная система счисления широко используется при задании различных оттенков цвета при кодировании графической информации (модель RGB). Так, в редакторе гипертекста Netscape Composer можно задавать цвета для фона или текста как в десятичной, так и шестнадцатеричной системах счисления.
Перевод чисел из одной системы счисления в другую
Наиболее часто встречающиеся системы счисления - это двоичная, шестнадцатеричная и десятичная. Как же связаны между собой представления числа в различных системах счисления? Рассмотрим различные способы перевода чисел из одной системы счисления в другую на конкретных примерах.
Пусть требуется перевести число 567 из десятичной в двоичную систему. Сначала определим максимальную степень двойки, такую, чтобы два в этой степени было меньше или равно исходному числу. В нашем случае это 9, т. к. 29=512, а 210=1024, что больше начального числа. Таким образом, мы получим число разрядов результата. Оно равно 9+1=10. Поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные цифры. Найдем вторую цифру результата. Возведем двойку в степень 9 и вычтем из исходного числа: 567-29=55. Остаток сравним с числом 28=256. Так как 55 меньше 256, то девятый разряд будет нулем, т. е. результат примет вид 10хххххххх. Рассмотрим восьмой разряд. Так как 27=128>55, то и он будет нулевым.
Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 25=32<55, поэтому шестой разряд равен 1 (результат 10001ххххх). Для остатка 55-32=23 справедливо неравенство 24=16<23, что означает равенство единице пятого разряда. Действуя аналогично, получаем в результате число 1000110111. Мы разложили данное число по степеням двойки:
567=1*29+0*28+0*27+0*26+1*25+1*24+0*23+1*22 +1*21+1*20
При другом способe перевода чисел используется операция деления в столбик. Рассмотрим то же самое число 567. Разделив его на 2, получим частное 283 и остаток 1. Проведем ту же самую операцию с числом 283. Получим частное 141, остаток 1. Опять делим полученное частное на 2, и так до тех пор, пока частное не станет меньше делителя. Теперь для того, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, то есть 1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.
Результат, естественно, не изменился: 567 в двоичной системе счисления записывается как 1000110111.
Эти два способа применимы при переводе числа из десятичной системы в систему с любым основанием. Для закрепления навыков рассмотрим перевод числа 567 в систему счисления с основанием 16.
Сначала осуществим разложение данного числа по степеням основания. Искомое число будет состоять из трех цифр, т. к. 162=256 < 567 < 163=4096. Определим цифру старшего разряда. 2*162=512<567<3*162=768, следовательно искомое число имеет вид 2хх, где вместо х могут стоять любые шестнадцатеричные цифры. Остается распределить по следующим разрядам число 55 (567-512). 3*16=48<55<4*16=64, значит во втором разряде находится цифра 3. Последняя цифра равна 7 (55-48). Искомое шестнадцатеричное число равно 237.
Второй способ состоит в осуществлении последовательного деления в столбик, с единственным отличием в том, что делить надо не на 2, а на 16, и процесс деления заканчивается, когда частное становится строго меньше 16.
Конечно, не надо забывать и о том, что для записи числа в шестнадцатеричной системе счисления, необходимо заменить 10 на A, 11 на B и так далее.
Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a0*pn + a1*pn-1 + ... + an-1*p1 + an*p0, где a0 ... an - это цифры данного числа в системе счисления с основанием p.
Пример. Переведем число 4A3F в десятичную систему. По определению, 4A3F= 4*163+A*162+3*16+F. Заменив A на 10, а F на 15, получим 4*163+10*162+3*16+15= 19007.
Пожалуй, проще всего осуществляется перевод чисел из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое двоичное число записать в системе счисления с основанием 2n, нужно
- данное двоичное число разбить справа налево на группы по n-цифр в каждой;
- если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов;
- рассмотреть каждую группу, как n-разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2n.
| 2-ная | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| 16-ная | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2-ная | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 16-ная | 8 | 9 | A | B | C | D | E | F |
Задания
- Переведите в десятичную систему счисления:
а) 100011102; б) 123458; в) AA02D34B16.
- Сравните два числа:
а) 10268 и 21616; б) 111112 и 111113.