Заполнение многоугольников и областей

Алгоритм с операцией XOR

Этот оригинальный алгоритм использует свойства операции XOR (исключающее ИЛИ ). Напомним, что XOR - бинарная операция над битами, действующая по правилу:

Рис. 6.4. XOR-растеризация.

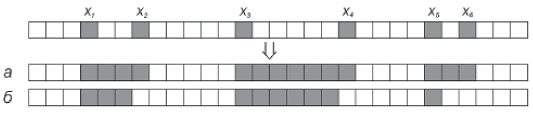
Пусть контур многоугольника растеризован и выведен на экран. Тогда его закрашивание сводится к заполнению в каждой строке растра всех промежутков вида [x_2i-1, x_2i], где через x_k обозначены x-координаты "включенных" пикселей в данной строке, упорядоченные по возрастанию (см. рис. 6.4а).

Через I(x, y) обозначим состояние пикселя с координатами (x, y): I(x, y) = 1, если пиксель "включен", и I(x, y) = 0 в противном случае. Нетрудно убедиться, что последовательное выполнение операции

I(x + 1, y) = I(x, y)  XOR  I(x + 1, y)

для x = 1, 2, 3, . . .X - 1 (где X - горизонтальный размер растра) приведет к требуемому результату - с той лишь разницей, что последний пиксель в каждом промежутке закрашен не будет (см. рис. 6.4б). Эта небольшая неточность в большинстве случаев некритична и визуально незаметна. Формально алгоритм записывается так:

Растеризовать контур многоугольника и вывести его на экран;
for(y = 1; y <= Y; y++)
      for(x = 1; x <= X - 1; x++)
            I(x + 1, y) = I(x + 1, y) XOR I(x, y);

Если же требуется получить результат, соответствующий рис. 6.4а, то можно либо после закрашивания повторно вывести на экран контур многоугольника, либо воспользоваться следующей модификацией приведенного алгоритма (называемой "XOR с флагом"):

Растеризовать контур многоугольника и вывести его на экран;

for(y = 1; y <= Y; y++)
{
      flag = 0;
      for(x = 1; x <= X; x++)
     {
            if( I(x, y) == 1 ) flag = 1 - flag;
            if( flag == 1 ) I(x, y) = 1;
      }
}

Достоинством алгоритмов XOR является их предельная простота. Недостаток - невозможность работы при наличии посторонних изображений на экране.

Исключительные случаи

Остановимся теперь на способах исключения случаев, приведенных на рис. 6.1. В случае горизонтального ребра, очевидно, достаточно при растеризации этого ребра вывести лишь его концы.

Для исключения остальных случаев можно поступить следующим образом. При растеризации каждого ребра многоугольника не будем выводить его нижний конец (x₂, y₂), а верхний конец выведем с помощью операции I(x₁, y₁) = I(x₂, y₂) XOR 1. Это приведет к тому, что верхние (нижние) концы ребер, попавшие в один и тот же пиксель, не будут выведены, а значит, "одиночные" точки в строках растра будут исключены.

Рис. 6.5. Шаги закрашивания многоугольника.

Алгоритм с операцией XOR с перегородкой

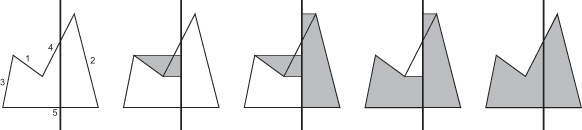
Алгоритм заключается в инвертировании цвета всех пикселей, расположенных правее i -го ребра, производимом последовательно для i = 1, 2, . . .N (порядок нумерации ребер не имеет значения). Горизонтальные ребра при этом игнорируются. Как видно из рис. 6.5, в результате закрашенными окажутся все внутренние пиксели многоугольника и только они.

К достоинствам данного алгоритма можно отнести его простоту и оригинальность, а также отсутствие дополнительных структур данных. Недостатком является необходимость выполнения большого числа операций с пикселями (до N операций с каждым пикселем), в том числе и вне многоугольника. В частности, чем больше расстояние между многоугольником и правой границей экрана, тем больше будет совершено "лишних" операций.

От этого недостатка свободна модификация данного алгоритма - "XOR-2 с перегородкой". Идея ее заключается в том, чтобы инвертировать область не между ребром и правой границей экрана, а между ребром и вертикальной прямой ("перегородкой"), мысленно проведенной в любом удобном месте - например пересекающей многоугольник (см. рис. 6.6).

Рис. 6.6. Растеризация с операцией XOR с перегородкой.