НОУ ИНТУИТ | Алгебра матриц и линейные пространства. Лекция 9: Проективная размерность подпространств и проективная геометрия. Теорема о ранге матрицы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 10.09.2007 | Доступ: свободный | Студентов: 3991 / 731 | Оценка: 4.33 / 3.93 | Длительность: 13:22:00

Тема: Математика

Специальности: Математик

Теги: beta, TE, алгебраическим дополнением, вычисления, геометрия, законы дистрибутивности, игры, линейная оболочка строк, матрица перехода, моноид, определитель матрицы, расширенная матрица, система линейных уравнений определенная, собственный вектор, теория, элементы

|

Вам нравится? Нравится 63 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Размерность пространства решений однородной системы линейных уравнений

Как мы отметили ранее, совокупность решений X_одн однородной системы линейных уравнений с матрицей $A=(a_{ij}) \in \mM_{m,n}(K)$ является линейным пространством, подпространством в Kⁿ.

Теорема 9.17.1. Если r=r(A)<n, то 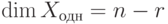$\dim X_{\textup{одн}}=n-r$ (т. е. размерность пространства решений равна числу свободных неизвестных). (Если r(A)=n, то система линейных уравнений имеет лишь нулевое решение.)

Доказательство. Для удобства записи переупорядочим неизвестные, если это необходимо, так, чтобы

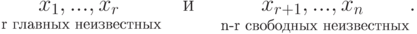
$\underset{\text{ r главных неизвестных}}{x_1,...,x_r} \quad \text{и}\quad \underset{\text{ n-r свободных неизвестных}}{x_{r+1},...,x_n}.$

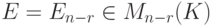Пусть $E=E_{n-r}\in M_{n-r}(K)$ - единичная матрица размера $(n-r)\times (n-r)$ . Возьмем ее строки в качестве наборов значений для свободных неизвестных и дополним их (единственно возможным способом) до решений нашей системы линейных уравнений

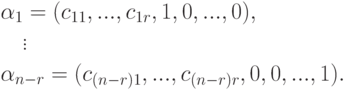
$\begin{align*} & \alpha_1 = (c_{11}, ..., c_{1r}, 1,0,...,0),\\ & \quad \vdots\\ & \alpha_{n-r} = (c_{(n-r)1},...,c_{(n-r)r},0,0,...,1). \end{align*}$

Эта система n-r строк-решений линейно независима (поскольку строки единичной матрицы, конечно, линейно независимы). Если

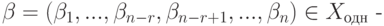
$\beta=(\beta_1,...,\beta_{n-r},\beta_{n-r+1},...,\beta_n)\in X_{\textup{одн}}\text{ -}$

произвольное решение, то

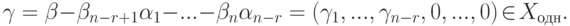
$\gamma=\beta-\beta_{n-r+1}\alpha_1-...-\beta_n\alpha_{n-r}= (\gamma_1,...,\gamma_{n-r},0,...,0)\!\in\! X_{\textup{одн}}.$

Однако, конечно,

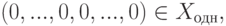
$(0,...,0,0,...,0)\in X_{\textup{одн}},$

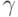при этом $\gamma$ и нулевое решение имеют одинаковый набор значений для свободных неизвестных. Так как значения главных неизвестных однозначно определяются по свободным, то 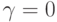$\gamma=0$ , следовательно,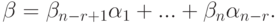

$\beta=\beta_{n-r+1}\alpha_1+...+\beta_n\alpha_{n-r}.$

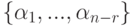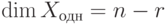Итак, мы построили базис $\{\alpha_1,...,\alpha_{n-r}\}$ линейного пространства решений X_одн , поэтому $\dim X_{\textup{одн}}=n-r$ .

Замечание 9.17.2. Если вместо строк единичной матрицы E_n-r для свободных неизвестных брать строки всевозможных матриц 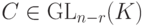$C\in\GL_{n-r}(K)$ (т. е. 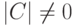$C\in M_{n}(K)$ , $|C|\neq 0$ ), то этот алгоритм позволяет построить все базисы в X_одн .

Замечание 9.17.2. Любой базис линейного пространства решений X_одн однородной системы линейных уравнений называется в ряде алгебраических текстов " фундаментальной системой решений однородной системы линейных уравнений ".

Задание любого подпространства в _K V = K^n как пространства решений однородной системы линейных уравнений

Пусть K - поле, 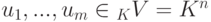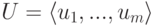$u_1,...,u_m\in {}_K V=K^n$ , $U=\langle u_1,...,u_m\rangle$ - подпространство в Kⁿ, являющееся линейной оболочкой строк u₁,...,u_m, т. е. множеством всех линейных комбинаций строк u₁,...,u_m. Мы найдем такую матрицу 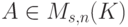$A\in M_{s,n}(K)$ , что множество решений однородной системы линейных уравнений

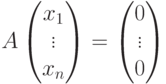
$A \begin{pmatrix} x_1\\ \vdots\\ x_n \end{pmatrix} = \begin{pmatrix} 0\\ \vdots\\ 0 \end{pmatrix}$

совпадает с U.

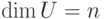Если U - нулевое подпространство, то в качестве A мы можем взять любую матрицу $n\times n$ с ненулевым определителем (например, A=E ). Если U=Kⁿ (это эквивалентно тому, что $\dim U=n$ ), то в качестве A мы можем взять нулевую матрицу из M_s,n, $s \geq 1$ . Если же $1 \leq \dim U = r(u_1,...,u_m)<n$ , то пусть u_i=(u_i1,u_i2,...,u_in), $1 \leq i \leq m$ , $u_{ij}\in K$ .

Рассмотрим матрицу 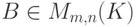$B\in M_{m,n}(K)$ , B=(b_ij), b_ij=u_ij, 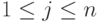$1 \leq i \leq m$ , $1 \leq j \leq n$ , и однородную систему линейных уравнений

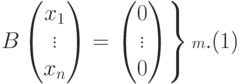$\begin{equation}\label{stelo} B \begin{pmatrix} x_1\\ \vdots\\ x_n \end{pmatrix} = \left. \begin{pmatrix} 0\\ \vdots\\ 0 \end{pmatrix} \right\}{\scriptstyle m}. \end{equation}$

( 9.2)

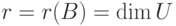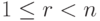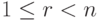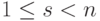Ясно, что $r=r(B)=\dim U$ , поэтому $1 \leq r < n$ . Размерность s пространства решений X__одн этой системы равна n-r, и так как $1 \leq r<n$ , то $1 \leq s<n$ .

Пусть строки 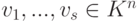$v_1,...,v_s\in K^n$ образуют фундаментальную систему решений системы (9.2), v_i=(v_i1,...,v_in), 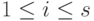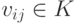$1 \leq i \leq s$ , $v_{ij}\in K$ . Пусть 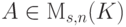$A\in \mM_{s,n}(K)$ , A=(a_ij), a_ij=v_ij, 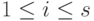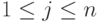$1 \leq i \leq s$ , $1 \leq j \leq n$ . Покажем, что A - искомая матрица.

Действительно, по построению матрицы A любая строка из U (как линейная комбинация строк u₁,...,u_m ) является решением однородной системы уравнений

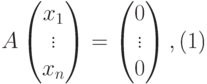$\begin{equation}\label{dusteloj} A \begin{pmatrix} x_1\\ \vdots\\ x_n \end{pmatrix} = \begin{pmatrix} 0\\ \vdots\\ 0 \end{pmatrix}, \end{equation}$

( 9.3)

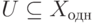т. е. $U\subseteq X_{\textup{одн}}$ . С другой стороны,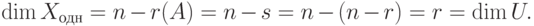

$\dim X_{\textup{одн}} = n-r(A) = n-s = n-(n-r) = r = \dim U.$

Следовательно, U=X_одн.

В заключение отметим, что матрица A определена неоднозначно. Например, другая матрица A' может быть получена с помощью другой фундаментальной системы решений системы (9.2).

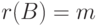Полученное задание линейных подпространств оказывается полезным при решении ряда практических задач. Например, пусть $u_1,...,u_m\in R^n$ - линейно независимые строки, m<n. Требуется найти такие строки u_m+1,...,u_n, что {u₁,...,u_n} - базис линейного пространства Rⁿ. Как и выше, пусть v₁,...,v_s - какая-нибудь фундаментальная система решений системы (9.2) (в нашем случае r(B)=m , s=n-m ). Положим u_m+1=v₁,...,u_n=v_n-m. Покажем, что {u₁,...,u_n} - базис в Rⁿ. Достаточно показать, что строки u₁,...,u_n линейно независимы над R. 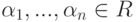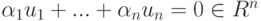Пусть $\alpha_1,...,\alpha_n\in R$ и $\alpha_1 u_1+...+\alpha_n u_n=0\in R^n$ . Тогда для строки

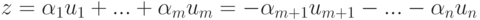
$z=\alpha_1 u_1+...+\alpha_m u_m=-\alpha_{m+1}u_{m+1}-...-\alpha_n u_n$

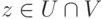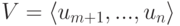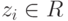имеем $z\in U\cap V$ , где $V=\langle u_{m+1},...,u_n\rangle$ . Если z=(z₁,...,z_n), $z_i\in R$ , $1 \leq i \leq n$ , то по построению подпространств U и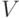

(см. (9.2), (9.3)) имеем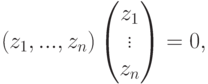

$(z_1,...,z_n) \begin{pmatrix} z_1\\ \vdots\\ z_n \end{pmatrix}=0,$

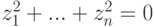, следовательно, z₁=...=z_n=0, и 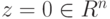$z=0\in R^n$ . Значит,

$\alpha_1 u_1+...+\alpha_m u_m=0 (\in R^n) = \alpha_{m+1}u_{m+1}+...+\alpha_nu_n.$

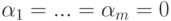Но u₁,...,u_m - линейно независимые строки, поэтому $\alpha_1=...=\alpha_m=0$ . Строки u_m+1,...,u_n также линейно независимы, следовательно, 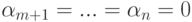$\alpha_{m+1}=...=\alpha_n=0$ . Итак, 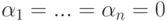$\alpha_1=...=\alpha_n=0$ и строки u₁,...,u_n линейно независимы.

Таким образом, мы рассмотрели два способа задания линейных подпространств в _K V=Kⁿ :

как множество решений X_одн однородной системы линейных уравнений;
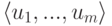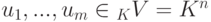как линейную оболочку $\langle u_1,...,u_m\rangle$ строк $u_1,...,u_m\in {}_K V=K^n$ .

При этом мы научились переходить от первого задания ко второму (фундаментальная система решений) и от второго задания к первому. Первый способ задания удобен для задания пересечения 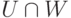$U\cap W$ подпространств (надо к первой однородной системе уравнений приписать вторую). Второй способ задания удобен для задания суммы подпространств:

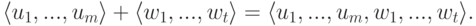
$\langle u_1,...,u_m\rangle+ \langle w_1,...,w_t\rangle= \langle u_1,...,u_m,w_1,...,w_t\rangle.$

В следующем примере мы увидим комбинацию этих приемов.

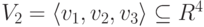Пример 9.18.1. Пусть $V_1=\langle u_1,u_2,u_3\rangle\subseteq R^4$ (линейная оболочка строк u₁=(1,1,0,0), u₂=(0,1,1,0), u₃=(0,0,1,1) ), $V_2=\langle v_1,v_2,v_3\rangle\subseteq R^4$ (линейная оболочка строк v₁=(1,0,1,0), v_2=(0,2,1,1), v₃=(1,2,1,2) ). Необходимо найти базисы линейных пространств V₁+V₂ и $V_1\cap V_2$ , при этом строки u₁, u₂, u₃, v₁, v₂, v₃ выразить через базис пространства V₁+V₂.

Решение Запишем строки u₁, u₂, u₃, v₁, v₂, v₃ по столбцам и приведем полученную матрицу к ступенчатому виду с помощью элементарных преобразований строк:

$\begin{mult} \begin{gathered} u_1\ u_2\ u_3\,\,\ \! v_1\ v_2\ v_3 \kern53mm \\ \left( \begin{array}{cccccc} 1 & 0 & 0 & 1 & 0 & 1\\ 1 & 1 & 0 & 0 & 2 & 2\\ 0 & 1 & 1 & 1 & 1 & 1\\ 0 & 0 & 1 & 0 & 1 & 2 \end{array}\right)\to \left( \begin{array}{cccccc} 1 & 0 & 0 & \phm 1 & 0 & 1\\ 0 & 1 & 0 & -1 & 2 & 1\\ 0 & 1 & 1 & \phm 1 & 1 & 1\\ 0 & 0 & 1 & \phm 0 & 1 & 2 \end{array}\right)\to{} \end{gathered} \\[3mm] \begin{gathered} \kern55mm u'_1\,\ u'_2\,\ u'_3\ \ \ v'_1\;\ \ \ v'_2\;\ \ \ v'_3 \\ {}\to \left( \begin{array}{cccccc} 1 & 0 & 0 & \phm 1 & \phm 0 & 1\\ 0 & 1 & 0 & -1 & \phm 2 & 1\\ 0 & 0 & 1 & \phm 2 & -1 & 0\\ 0 & 0 & 1 & \phm 0 & \phm 1 & 2 \end{array}\right)\to \left( \begin{array}{cccccc} \multicolumn{1}{|c}{1} & 0 & 0 & \phm 1 & \phm 0 & \phm 1\\ \cline{1-1} 0 & \multicolumn{1}{|c}{1} & 0 & -1 & \phm 2 & \phm 1\\ \cline{2-2} 0 & 0 & \multicolumn{1}{|c}{1} & \phm 2 & -1 & \phm 0\\ \cline{3-3} 0 & 0 & 0 & \multicolumn{1}{|c}{\phm 1} & -1 & -1\\ \cline{4-6} \end{array}\right). \end{gathered} \end{mult}$

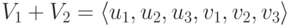Поскольку $V_1+V_2=\langle u_1,u_2,u_3,v_1,v_2,v_3\rangle$ и элементарные преобразования строк матрицы не меняют линейных соотношений между столбцами, то {u₁,u₂,u₃,v₁} - базис в V_1+V_2 (и так как $\dim (V_1+V_2)=4$ , то V₁+V₂= R^4 ). Из ступенчатого вида мы вычисляем v'₂ и v'₃ через u'₁, u'₂, u'₃, v'₁ :

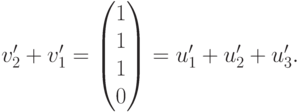
$v'_2+v'_1= \begin{pmatrix} 1\\ 1\\ 1\\ 0 \end{pmatrix}= u'_1+u'_2+u'_3.$

Поэтому v'_2=u'_1+u'_2+u'_3-v'_1 и, следовательно, v₂=u₁+u₂+u₃-v₁. Для v'₃ мы видим, что v'₃+v'₁=(2,0,2,0)^*=2u'₁+2u'₃, поэтому v₃=2u₁+2u₃-v₁. Проведенные вычисления равносильны завершению приведения матрицы к главному ступенчатому виду:

$\left( \begin{array}{cccccc} \multicolumn{1}{|c}{1} & 0 & 0 & 0 & \phm 1 & \phm 2\\ \cline{1-1} 0 & \multicolumn{1}{|c}{1} & 0 & 0 & \phm 1 & \phm 0\\ \cline{2-2} 0 & 0 & \multicolumn{1}{|c}{1} & 0 & \phm 1 & \phm 2\\ \cline{3-3} 0 & 0 & 0 & \multicolumn{1}{|c}{\phm 1} & -1 & -1\\ \cline{4-6} \end{array}\right).$

Рассмотрим теперь $V_1\cap V_2$ . Для этого найдем однородные системы линейных уравнений, чьи множества решений совпадают с V₁ и V₂ соответственно.

Для V₁:

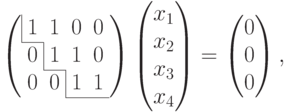
$\left( \begin{array}{cccc} \multicolumn{1}{|c}{1} & 1 & 0 & 0\\ \cline{1-1} 0 & \multicolumn{1}{|c}{1} & 1 & 0\\ \cline{2-2} 0 & 0 & \multicolumn{1}{|c}{1} & 1\\ \cline{3-4} \end{array} \right) \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix},$

система уже имеет ступенчатый вид, x₁, x₂, x₃ - главные неизвестные, x₄ - свободная. Фундаментальная система решений состоит из одной строки (-1,1,-1,1). Итак, подпространство V₁ совпадает с пространством решений однородной системы линейных уравнений

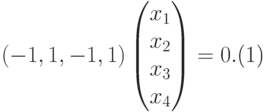$\begin{equation}\label{denovestelo} (-1,1,-1,1) \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} = 0. \end{equation}$

( 9.4)

Для V₂ :

$\begin{align*} & \begin{pmatrix} 1 & 0 & 1 & 0\\ 0 & 2 & 1 & 1\\ 1 & 2 & 1 & 2 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \to \begin{pmatrix} 1 & 0 & 1 & 0\\ 0 & 2 & 1 & 1\\ 0 & 2 & 0 & 2 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \to{} \\[1mm] & \quad {}\to \begin{pmatrix} 1 & 0 & 1 & 0\\ 0 & 2 & 1 & 1\\ 0 & 1 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} \!=\! \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \to\! %{} %\\[3mm] %& \quad {}\to \begin{pmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1\\ 0 & 2 & 1 & 1 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} \!=\! \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \to{} \\[1mm] & \quad {}\to \left( \begin{array}{cccc} \multicolumn{1}{|c}{1} & 0 & 1 & \phm 0\\ \cline{1-1} 0 & \multicolumn{1}{|c}{1} & 0 & \phm 1\\ \cline{2-2} 0 & 0 & \multicolumn{1}{|c}{1} & -1\\ \cline{3-4} \end{array}\right) \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix}, \end{align*}$

и мы приходим к ступенчатому виду, при этом x₁, x₂, x₃ - главные неизвестные, а x₄ - свободная. Фундаментальная система решений состоит из одной строки (-1,-1,1,1). Значит, однородная система линейных уравнений

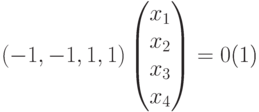$\begin{equation}\label{denovedusteloj} (-1,-1,1,1) \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} = 0 \end{equation}$

( 9.5)

задает подпространство V₂.

Ясно, что система

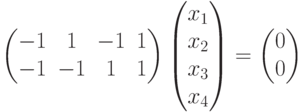
$\begin{pmatrix} -1 & \phm 1 & -1 & 1 \\ -1 & -1 & \phm 1 & 1 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \end{pmatrix}$

задает подпространство $V_1\cap V_2$ .

Решим эту систему:

$\begin{align*} & \begin{pmatrix} -1 & \phm 1 & -1 & 1\\ -1 & -1 & \phm 1 & 1 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix} \to{} \\[1mm] & \quad {}\to \begin{pmatrix} \phm 1 & -1 & 1 & -1\\ -1 & -1 & 1 & \phm 1 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix} \to{} \\[1mm] & \quad {}\to \left( \begin{array}{cccc} \multicolumn{1}{|c}{1} & -1 & 1 & -1\\ \cline{1-1} 0 & \multicolumn{1}{|c}{-2} & 2 & \phm 0\\ \cline{2-4} \end{array}\right) \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix}, \end{align*}$

x₁, x₂ - главные неизвестные, x₃, x₄ - свободные неизвестные. Фундаментальная система решений состоит из двух строк

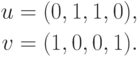
$\begin{align*} u &= (0,1,1,0),\\ v &= (1,0,0,1). \end{align*}$

Следовательно, {u,v} - базис линейного подпространства $V_1\cap V_2$ .

Дальше >>

Авторизоваться

Алгебра матриц и линейные пространства

Проективная размерность подпространств и проективная геометрия. Теорема о ранге матрицы

Размерность пространства решений однородной системы линейных уравнений

Задание любого подпространства в _K V = K^n как пространства решений однородной системы линейных уравнений

Вопросы и ответы