|
Здравствуйте! Записался на ваш курс, но не понимаю как произвести оплату. Надо ли писать заявление и, если да, то куда отправлять? как я получу диплом о профессиональной переподготовке? |
Переход от данных к конечному автомату
Таблицы переходов и состояний представляют собой метод программирования не только для задач, которые сводятся к конечным автоматам. При обсуждении XML/XSL-подхода к задаче стандартизованного представления таблиц переходов были указаны возможности применения методики оперирования со структурными представлениями данных и программ для более широкого класса алгоритмов.
Однако мы пока не решали задачи, когда представление алгоритма зависит от входных данных. Она классифицирована для автоматов как задача динамического порождения автомата (см.  9.3, пункт 3). Конечно же, под таким углом зрения можно рассматривать трансляцию: текстовый файл на входном языке есть часть данных, генерирующая план обработки другой части данных, которая предъявляется при решении конкретной задачи. Вторая задача подобного типа, для которой разработаны методы, — это задача специализации универсальной программы. Она также может рассматриваться как уточнение общего плана, исходя из частичного знания обрабатываемых данных. Упомянутые случаи характеризуются тем, что представление алгоритма, зависящее от части входных данных, строится из заранее определенных заготовок. Например, для трансляции такими заготовками являются алгоритмы выполнения абстрактно-синтаксического представления программы.
9.3, пункт 3). Конечно же, под таким углом зрения можно рассматривать трансляцию: текстовый файл на входном языке есть часть данных, генерирующая план обработки другой части данных, которая предъявляется при решении конкретной задачи. Вторая задача подобного типа, для которой разработаны методы, — это задача специализации универсальной программы. Она также может рассматриваться как уточнение общего плана, исходя из частичного знания обрабатываемых данных. Упомянутые случаи характеризуются тем, что представление алгоритма, зависящее от части входных данных, строится из заранее определенных заготовок. Например, для трансляции такими заготовками являются алгоритмы выполнения абстрактно-синтаксического представления программы.
В данном разделе показан иной метод построения алгоритма, зависящего от входных данных. Его идея в том, чтобы составить такое представление алгоритма, которое допускает непосредственную интерпретацию. Естественный путь демонстрации метода — взять за основу известный класс алгоритмов, конкретный представитель которого выбирается, исходя из знания о входных данных.
Обратимся к задаче, которая для каждого конкретного случая решается с помощью конечного автомата специального вида (как и всегда, выбор конкретного представления существенно влияет на сложность и другие характеристики программы, автоматическое применение ранее использованных представлений в других задачах не рекомендуется).
Пусть требуется подсчитать, сколько раз каждое из вводимых слов встречается в некотором большом файле (теперь слово — это любая последовательность символов). 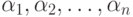 — вводимые слова;
— вводимые слова; 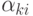 — слово. Напечатать:
— слово. Напечатать:
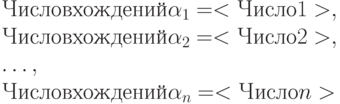
Где <Число k> — полное число вхождений слова 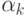 в файл с учетом возможного перекрытия слов (например, в строке *МАМАМА{} два вхождения слова МАМА ).
в файл с учетом возможного перекрытия слов (например, в строке *МАМАМА{} два вхождения слова МАМА ).
Для заданных заранее слов легко построить граф, каждая вершина которого представляет символы внутри слов. Его вершины помечены символом. Из такой вершины исходят две дуги: первая указывает на вершину, к которой следует переходить, когда очередной читаемый символ совпадает с пометкой вершины, а вторая — на ту, которая должна стать преемником данной в случае несовпадения. Легко видеть, что это одна из форм представления конечного автомата, каждое состояние которого кодирует множество всех вершин, связанных дугами второго вида, а состояния-преемники определяются дугами первого вида исходного графа. Для того, чтобы этот автомат работал (решал поставленную задачу), нужно снабдить его действиями, которые сводятся к увеличению счетчиков, соответствующих найденным словам, а также определить начальное и конечное состояния. Мы не будем переделывать исходный граф, поскольку такая его форма удобнее для интерпретации.
Если дуги первого вида изображать стрелками, исходящими в горизонтальном направлении, дуги второго вида — вертикальными стрелками, а действия со счетчиками — соответствующими пометками при дугах, то, например, для множества слов
- МАМА,
- МАШИНА,
- ШИНА,
- МАТ,
- НА
может быть построен граф, показанный на рис. 12.1.
На языке С++/C# структура, которая представляет граф, подобный только что описанному, может быть изображена следующим образом:
struct union { char Symb;
struct {
bool Tag; // поле признака текущего
// значения в union:
union {
char Symb; // <- Tag = true
int Num; // <- Tag = false
}; // имя объединения здесь
// не нужно
int yes; // индекс перехода по совпадению
int no; // индекс перехода по несовпадению
} Table[];Особенность данной интерпретации таблицы в том, что она соответствует автоматам Мура: действия ассоциируются с вершинами, а не с дугами, с состояниями, а не с переходами. Вершина, которой сопоставлено действие, не требует чтения очередного символа и его анализа. Вместо символьных пометок вершины-действия содержат числовые номера, идентифицирующие соответствующие счетчики (размеченное объединение использовано для того, чтобы отразить это соглашение).