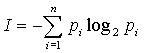Меры информации в системе

2. Мера К. Шеннона. Формула Шеннона дает оценку информации независимо, отвлеченно от ее смысла:

где n - число состояний системы; р_i - вероятность (или относительная частота) перехода системы в i-е состояние, причем сумма всех p_i равна 1.

Если все состояния равновероятны (т.е. р_i=1/n ), то I=log₂n.

К. Шенноном доказана теорема о единственности меры количества информации. Для случая равномерного закона распределения плотности вероятности мера Шеннона совпадает с мерой Хартли. Справедливость и достаточная универсальность формул Хартли и Шеннона подтверждается и данными нейропсихологии.

Пример. Время t реакции испытуемого на выбор предмета из имеющихся N предметов линейно зависит от log₂N: t=200+180log₂N (мс). По аналогичному закону изменяется и время передачи информации в живом организме. Один из опытов по определению психофизиологических реакций человека состоял в том, что перед испытуемым большое количество раз зажигалась одна из n лампочек, на которую он должен был указать в ходе эксперимента. Оказалось, что среднее время, необходимое для правильного ответа испытуемого, пропорционально не числу n лампочек, а именно величине I, определяемой по формуле Шеннона, где p_i - вероятность зажечь лампочку номер i

Легко видеть, что в общем случае

Если выбор i-го варианта предопределен заранее (выбора, собственно говоря, нет, p_i=1 ), то I=0.

Сообщение о наступлении события с меньшей вероятностью несет в себе больше информации, чем сообщение о наступлении события с большей вероятностью. Сообщение о наступлении достоверно наступающего события несет в себе нулевую информацию (и это вполне ясно: событие всё равно произойдет когда-либо).

Пример. Если положение точки в системе известно, в частности, она - в k-ой клетке, т.е. все р_i=0, кроме р_k=1, то тогда I=log₂1=0 и мы здесь новой информации не получаем (как и следовало ожидать).

Пример. Выясним, сколько бит информации несет произвольное двузначное число со всеми значащими цифрами (отвлекаясь при этом от его конкретного числового значения, т.е. каждая из возможных цифр может появиться на данном месте, в данном разряде с одинаковой вероятностью). Так как таких чисел может быть всего 90 (10-99), то информации будет количество I=log₂90 или приблизительно I=6,5. Так как в таких числах значащая первая цифра имеет 9 значений (1-9), а вторая - 10 значений (0-9), то I=log₂90=log₂9+log₂10. Приблизительное значение log₂10 равно 3,32. Итак, сообщение в одну десятичную единицу несет в себе в 3,32 больше информации, чем в одну двоичную единицу (чем log₂2=1 ), а вторая цифра, например, в числе аа, несет в себе больше информации, чем первая (если цифры а обоих разрядов неизвестны; если же эти цифры а известны, то выбора нет и информация равна нулю).

Если в формуле Шеннона обозначить f_i=-nlog₂ p_i, то получим, что I можно понимать как среднеарифметическое величин f_i.

Отсюда, f_i можно интерпретировать как информационное содержание символа алфавита с индексом i и величиной p_i вероятности появления этого символа в сообщении, передающем информацию.

Пример. Пусть рассматривается алфавит из двух символов русского языка - "к" и "а". Относительные частоты встречаемости этих букв в частотном словаре русского языка равны соответственно p₁=0.028, p₂=0.062. Возьмем произвольное слово p длины N из k букв "к" и m (k+m=N) букв "а" над этим алфавитом. Число всех таких возможных слов, как это следует из комбинаторики, равно n=N!/(k! m!). Оценим количество информации в таком слове: I=log₂n=lnn/ln2=log₂e[lnN!-lnk!-lnm!]. Используя известную формулу Стирлинга (эта формула, как известно из математического анализа, достаточно точна при больших N, например, при N>100 ) - 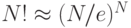), а точнее, ее важное следствие, - 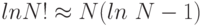), получаем оценку количества информации (в битах) на 1 символ любого слова:

Пример. В сообщении 4 буквы "a", 2 буквы "б", 1 буква "и", 6 букв "р". Определим количество информации в одном таком (из всех возможных) сообщений. Число N различных сообщений длиной 13 букв будет равно величине: N=13!/(4!x2!x1!x6!)=180180. Количество информации I в одном сообщении будет равно величине: 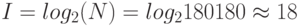(бит).

Если k - коэффициент Больцмана, известный в физике как k=1.38x10^-16 эрг/град, то выражение

в термодинамике известно как энтропия, или мера хаоса, беспорядка в системе. Сравнивая выражения I и S, видим, что I можно понимать как информационную энтропию ( энтропию из-за нехватки информации о/в системе).

Л. Больцман дал статистическое определение энтропии в 1877 г. и заметил, что энтропия характеризует недостающую информацию. Спустя 70 лет, К. Шеннон сформулировал постулаты теории информации, а затем было замечено, что формула Больцмана инвариантна информационной энтропии, и была выявлена их системная связь, системность этих фундаментальных понятий.

Важно отметить следующее.

Нулевой энтропии соответствует максимальная информация. Основное соотношение между энтропией и информацией:

I+S(log2e)/k=const

или в дифференциальной форме

dI/dt= -((log2e)/k)dS/dt.

При переходе от состояния S₁ с информацией I₁ к состоянию S₂ с информацией I₂ возможны случаи:

1. S₁ < S₂ (I₁ >I₂) - уничтожение (уменьшение) старой информации в системе;
2. S₁ = S₂ (I₁ = I₂) - сохранение информации в системе;
3. S₁ > S₂ (I₁ < I₂) - рождение новой (увеличение) информации в системе.

Главной положительной стороной формулы Шеннона является ее отвлеченность от семантических и качественных, индивидуальных свойств системы. В отличие от формулы Хартли, она учитывает различность, разновероятность состояний - формула имеет статистический характер (учитывает структуру сообщений), делающий эту формулу удобной для практических вычислений. Основной отрицательной стороной формулы Шеннона является то, что она не различает состояния (с одинаковой вероятностью достижения, например), не может оценивать состояния сложных и открытых систем и применима лишь для замкнутых систем, отвлекаясь от смысла информации. Теория Шеннона разработана как теория передачи данных по каналам связи, а мера Шеннона - мера количества данных и не отражает семантического смысла.

Увеличение (уменьшение) меры Шеннона свидетельствует об уменьшении (увеличении) энтропии (организованности) системы. При этом энтропия может являться мерой дезорганизации систем от полного хаоса ( S=S^max ) и полной информационной неопределенности ( I=I^min ) до полного порядка ( S=S^min ) и полной информационной определённости ( I=I^max ) в системе.