|
Хотелось бы иметь возможность читать текст сносок при использовании режима "Версия для печати" |
Проектирование реляционных баз данных на основе принципов нормализации: дальнейшая нормализация
Многозначные зависимости. Теорема Фейджина. Четвертая нормальная форма
Заметим, что последний вариант переменной отношения СЛУЖ_ПРО_ЗАДАН находится в BCNF, поскольку все атрибуты заголовка отношения входят в состав единственно возможного ключа. В этом отношении вообще отсутствуют нетривиальные FD. Поэтому ранее обсуждавшиеся принципы нормализации здесь неприменимы, но, тем не менее, мы получили полезную декомпозицию. Все дело в том, что в случае четвертого варианта отношения СЛУЖ_ПРО_ЗАДАН мы имеем дело с новым видом зависимости, впервые обнаруженным Роном Фейджином в 1971 г. Фейджин назвал зависимости этого вида многозначными (multi-valued dependency – MVD). Как мы увидим немного позже, MVD является обобщением понятия FD.
В отношении СЛУЖ_ПРО_ЗАДАН выполняются две MVD: СЛУ_НОМ->->ПРО_НОМ и СЛУ_НОМ->->СЛУ_ЗАДАН. Первая MVD означает, что каждому значению атрибута СЛУ_НОМ соответствует определяемое только этим значением множество значений атрибута ПРО_НОМ. Другими словами, в результате вычисления алгебраического выражения
(СЛУЖ_ПРО_НОМ WHERE (СЛУ_НОМ = сн AND СЛУ_ЗАДАН = сз)) PROJECT {ПРО_НОМ}
для фиксированного допустимого значения сн и любого допустимого значения сз мы всегда получим одно и то же множество значений атрибута ПРО_НОМ. Аналогично трактуется вторая MVD.
В переменной отношения r с атрибутами A, B, C (в общем случае, составными) имеется многозначная зависимость B от A (A->->B) в том и только в том случае, когда множество значений атрибута B, соответствующее паре значений атрибутов A и C, зависит от значения A и не зависит от значения C .
Многозначные зависимости обладают интересным свойством "двойственности", которое демонстрирует следующая лемма.
Лемма Фейджина
В отношении r {A, B, C} выполняется MVD A->->B в том и только в том случае, когда выполняется MVD A->->C.
Доказательство достаточности условия леммы. Пусть выполняется MVD A->->B. Пусть имеется некоторое удовлетворяющее этой зависимости значение Vr переменной отношения r, a обозначает значение атрибута A в некотором кортеже тела Vr, а {b} – множество значений атрибута B, взятых из всех кортежей тела Vr, в которых значением атрибута A является a. Предположим, что для этого значения a MVD A->->C не выполняется. Это означает, что существуют такое допустимое значение c атрибута C и такое значение 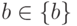 , что кортеж
, что кортеж 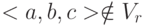 . Но это противоречит наличию MVD A->->B. Следовательно, если выполняется MVD A->->B, то выполняется и MVD A->->C. Аналогично можно доказать необходимость условия леммы.
. Но это противоречит наличию MVD A->->B. Следовательно, если выполняется MVD A->->B, то выполняется и MVD A->->C. Аналогично можно доказать необходимость условия леммы.
Таким образом, MVD A->->B и A->->C всегда составляют пару. Поэтому обычно их представляют вместе в форме A ->-> B | C.
FD является частным случаем MVD, когда множество значений зависимого атрибута обязательно состоит из одного элемента. Таким образом, если выполняется FD A->B, то выполняется и MVD A->->B . 1Упражнение по ходу лекции. Пусть имеется отношение r с атрибутами A, B, C (в общем случае, составными), в котором существует FD A->B. Что в этом случае можно сказать про зависимость атрибутов A и C ?
Мы видим, что отношения СЛУЖ_ПРО_НОМ и СЛУЖ_ЗАДАНИЕ не содержат MVD, отличных от FD, и именно в этом выигрывает декомпозиция из рис. 8.2. Правомочность этой декомпозиции доказывается приведенной ниже теоремой Фейджина, которая является уточнением и обобщением теоремы Хита.
Теорема Фейджина
Пусть имеется переменная отношения r с атрибутами A, B, C (в общем случае, составными). Отношение r декомпозируется без потерь на проекции {A, B} и {A, C} тогда и только тогда, когда для него выполняется MVD A ->-> B | C.
Докажем достаточность условия теоремы. Пусть Vr является некоторым допустимым значением переменной отношений r. Пусть a есть значение атрибута A в некотором кортеже тела Vr, {b} – множество значений атрибута B, взятых из всех кортежей тела Vr, в которых значением атрибута A является a, и {c} – множество значений атрибута C, взятых из всех кортежей тела Vr, в которых значением атрибута A является a. Тогда очевидно, что в тело значения переменной отношения r PROJECT {A, B} будут входить все кортежи вида {a, bi}, где  , и если некоторый кортеж {a, bj} входит в тело значения переменной отношения r PROJECT {A, B}, то
, и если некоторый кортеж {a, bj} входит в тело значения переменной отношения r PROJECT {A, B}, то 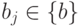 . Аналогичные рассуждения применимы к r PROJECT {A, C}. Очевидно, что из этого следует, что при наличии многозначной зависимости A ->-> B | C в переменной отношения r{A, B, C} декомпозиция r на проекции r PROJECT {A, B} и r PROJECT {A, C} является декомпозицией без потерь.
. Аналогичные рассуждения применимы к r PROJECT {A, C}. Очевидно, что из этого следует, что при наличии многозначной зависимости A ->-> B | C в переменной отношения r{A, B, C} декомпозиция r на проекции r PROJECT {A, B} и r PROJECT {A, C} является декомпозицией без потерь.
Для доказательства необходимости условия теоремы предположим, что декомпозиция переменной отношения r {A, B, C} на проекции r PROJECT {A, B} и r PROJECT {A, C} является декомпозицией без потерь для любого допустимого значения Vr переменной отношения r. Мы должны показать, что в теле Br значения-отношения Vr поддерживается ограничение
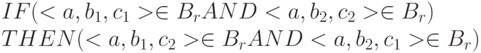
Действительно, пусть в Br входят кортежи <a, b1, c1> и <a, b2, c2>. Предположим, что 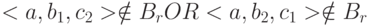 . Но в тело значения переменной отношения r PROJECT {A, B} входят кортежи <a, b1> и <a, b2>, а в тело значения переменной отношения r PROJECT {A, C} – <a, c1> и <a, c2>. Очевидно, что в тело значения естественного соединения r PROJECT {A, B} NATURAL JOIN r PROJECT {A, C} войдут кортежи <a, b1, c2> и <a, b2, c1>, и наше предположение об отсутствии по крайней мере одного из этих кортежей в Br противоречит исходному предположению о том, что декомпозиция r на проекции r PROJECT {A, B} и r PROJECT {A, C} является декомпозицией без потерь. Тем самым, теорема Фейджина полностью доказана. Конец доказательства.
. Но в тело значения переменной отношения r PROJECT {A, B} входят кортежи <a, b1> и <a, b2>, а в тело значения переменной отношения r PROJECT {A, C} – <a, c1> и <a, c2>. Очевидно, что в тело значения естественного соединения r PROJECT {A, B} NATURAL JOIN r PROJECT {A, C} войдут кортежи <a, b1, c2> и <a, b2, c1>, и наше предположение об отсутствии по крайней мере одного из этих кортежей в Br противоречит исходному предположению о том, что декомпозиция r на проекции r PROJECT {A, B} и r PROJECT {A, C} является декомпозицией без потерь. Тем самым, теорема Фейджина полностью доказана. Конец доказательства.
Теорема Фейджина обеспечивает основу для декомпозиции отношений, удаляющей "аномальные" многозначные зависимости, с приведением отношений в четвертую нормальную форму.
Переменная отношения r находится в четвертой нормальной форме (4NF) в том и только в том случае, когда она находится в BCNF, и все MVD r являются FD с детерминантами – возможными ключами отношения r .
В сущности, 4NF является BCNF, в которой многозначные зависимости вырождаются в функциональные (позволим себе на один момент отказаться от сокращений). Понятно, что отношение СЛУЖ_ПРО_ЗАДАН не находится в 4NF, поскольку детерминант MVD СЛУ_НОМ->->ПРО_НОМ и СЛУ_НОМ->->СЛУ_ЗАДАН не является возможным ключом, и эти MVD не являются функциональными. С другой стороны, отношения СЛУЖ_ПРО_НОМ и СЛУЖ_ЗАДАНИЕ находятся в BCNF и не содержат MVD, отличных от FD с детерминантом – возможным ключом. Поэтому они находятся в 4NF.
