Проецирование пространственных сцен
Проекция Меркатора
В XVI веке фламандский картограф Герхард Меркатор создал знаменитую цилиндрическую проекцию, обладающую свойством конформности. Конформность в проекции Меркатора достигается за счет растягивания цилиндра за полюсы, при этом в верхней и нижней части этого цилиндра масштаб становится очень искаженным. Несмотря на это данная проекция обладает одним замечательным свойством, очень нужным для навигаторов: прямая, проведенная через любые две точки на карте, является локсодромой, или линией постоянного румба. Локсодрома на сфере или какой-либо другой поверхности вращения пересекает все меридианы под постоянным углом (рис. 7.10).
Проекция Меркатора задается следующими формулами:
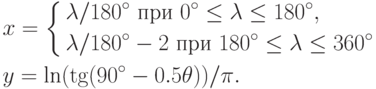
увеличить изображение
Рис. 7.10. Конформная проекция Меркатора. На карту нанесены локсодромы из Нью-Йорка
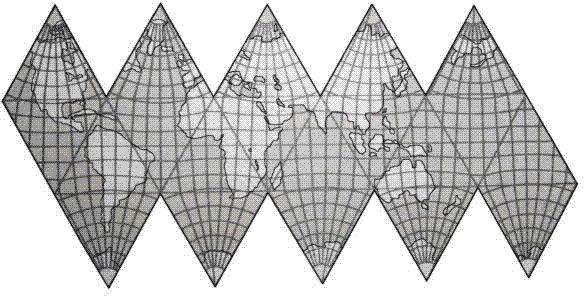
Проекции на многогранник
Будем называть разрезанной карту мира, спроецированную на тот или иной узор из каких-либо многоугольников. После складывания этих фрагментов образуется карта с разрывами любой части земного шара. Одну такую конформную карту составил философ и математик Ч.Пирс. Земная поверхность спроецирована на этой карте на восемь равнобедренных треугольников, которые можно рассматривать как грани октаэдра, сплющиваемого до тех пор, пока длина его пространственной диагонали не обратится в нуль. Вершинам нулевой диагонали на карте Пирса соответствуют северный и южный полюсы.
Примерно в то же время аналогичная идея пришла в голову выдающемуся экономисту из Йельского университета Ирвингу Фишеру: он задумал осуществить гномоническую проекцию поверхности Земли на 20 треугольных гранях икосаэдра (рис. 7.11). Икосаэдр является наиболее близким к идеалу многогранником для разрезания "на карты".
Необычные проекции
Картографы придумывали самые разнообразные виды проекций, порой удивительно выглядящие и при этом обладающие довольно неплохими свойствами. Одну из таких карт в форме кардиоиды (сердца) придумал Иоганн Вернер. Эта карта сохраняет площади. Она пользовалась широкой известностью в XVI в., но сейчас ею уже давно не пользуются. В отчете о картографических курьезах, написанном для внутреннего пользования фирмы "Лаборатории Белла", математик Эдгар Н. Гильберт пишет: "...незаслуженно забыта. Сильно искаженные части карты лежат далеко от основных масс суши. Искривленные параллели придают карте приятную иллюзию округлости... Параллели представляют собой дуги окружностей, расположенные на одинаковом расстоянии друг от друга, с центром в северном полюсе. Меридианы, проведенные для указа¬ния расстояний вдоль параллелей, такие же как на сфере".
Скопление материков на карте Вернера отражает неравномерное распределение суши по поверхности Земли. Тихий океан столь велик, что если смотреть на Землю из точки, расположенной над проливом Ла-Манш, то взгляду откроется около 80% всей суши, а противопо¬ложное полушарие будет почти сплошь покрыто водой
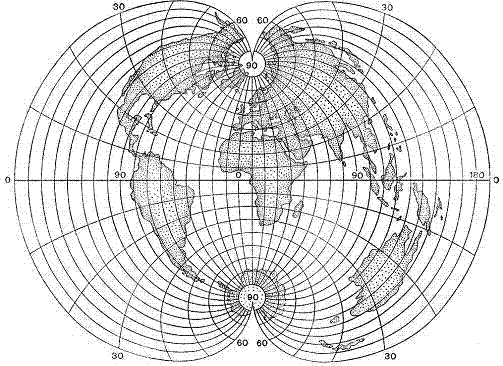
Довольно необычна поликоническая картографическая проекция - картографическая проекция, строящаяся с помощью ряда конусов, касательных к земному эллипсоиду (шару). В поликонической картографической проекции параллели нормальной сетки - дуги эксцентрических окружностей, осевой меридиан - прямая, на которой расположены центры параллелей, а остальные меридианы - кривые (рис. 7.12).
Вопросы и упражнения
- Назовите два основных вида проекций, определяемых типом пучка лучей.
- Назовите четыре вида параллельных проекций.
- Сколько шагов в алгоритме ортогональной проекции на произвольную плоскость?
- Какой вид имеет матрица косоугольной проекции на плоскость
 , переводящей вектор
, переводящей вектор 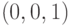 в вектор
в вектор  ?
? - Напишите формулы преобразования координат при центральной проекции на плоскость
 с центром в точке
с центром в точке 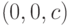 . Как выглядит матрица такой проекции в однородной системе координат?
. Как выглядит матрица такой проекции в однородной системе координат? - Что такое перспективное укорачивание?
- Что такое точка схода?
- Как реализуется проекция с тремя точками схода?
- Каким свойством обладает конформная проекция?
- Каким свойством обладает цилиндрическая проекция?
- В чем ценность проекции Меркатора?
- Какой многогранник наиболее удобен для построения разрезанных карт?