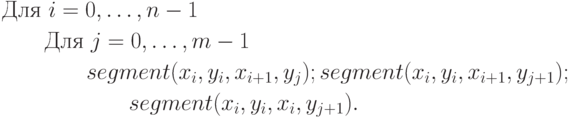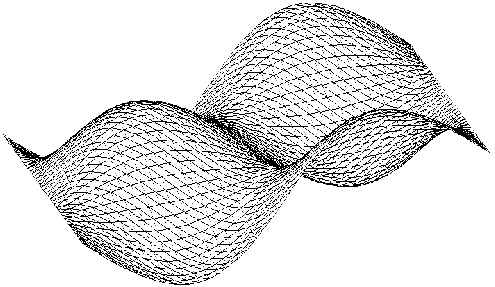Удаление невидимых поверхностей и линий

Методы приоритетов (художника, плавающего горизонта)

Здесь мы рассмотрим группу методов, учитывающих специфику изображаемой сцены для удаления невидимых линий и поверхностей.

При изображении сцен со сплошным закрашиванием поверхностей можно воспользоваться методом художника: элементы сцены изображаются в последовательности от наиболее удаленных от наблюдателя к более близким. При экранировании одних участков сцены другими невидимые участки просто закрашиваются. Если вычислительная трудоемкость получения изображения для отдельных элементов достаточно высока, то такой алгоритм будет не самым лучшим по эффективности, но зато мы избежим анализа (и вполне возможно, тоже дорогостоящего), позволяющего установить, какие же из элементов изображать не надо в силу их невидимости. Например, при изображении правильного многогранника мы довольно легко можем упорядочить его грани по глубине, но такая сортировка для произвольного многогранника возможна далеко не всегда. Мы рассмотрим применение этого метода на примере изображения поверхности, заданной в виде однозначной функции двух переменных.

Пусть поверхность задана уравнением

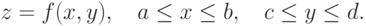
В качестве картинной плоскости выберем плоскость . В области задания функции на осях координат построим сетку узлов: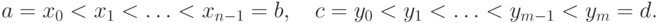

Тогда 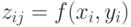представляют собой набор "высот" для данной поверхности по отношению к плоскости . Поверхность будем аппроксимировать треугольниками с вершинами в точках 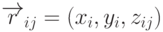так, что каждому прямоугольнику сетки узлов будут соответствовать два треугольника: и . Для построения наглядного изображения поверхности повернем ее на некоторый угол сначала относительно оси 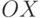, а затем относительно оси 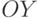, причем направление вращения выберем таким образом, что точки, соответствующие углам координатной сетки, расположатся в следующем порядке по удаленности от картинной плоскости: 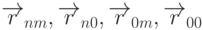, т.е. точка окажется наиболее близкой к картинной плоскости (и наиболее удаленной от наблюдателя). Предполагается, что способ закрашивания треугольников уже определен. Тогда процесс изображения поверхности можно коротко записать так:

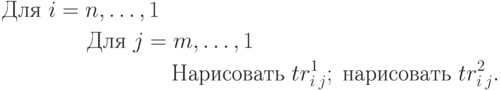
При такой последовательности вывода изображения мы продвигаемся от самого удаленного треугольника к все более близким, частично закрашивая уже изображенные участки поверхности.

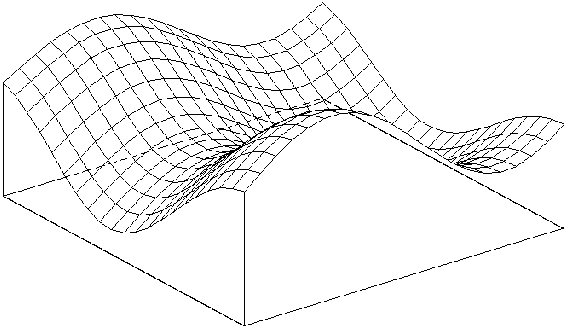
Алгоритм художника можно применять для полностью закрашенной сцены, а для каркасного изображения, когда объект представляется в виде набора кривых или ломаных линий, он непригоден. Для этого случая предложен еще один метод, весьма эффективный - метод плавающего горизонта. Вернемся к предыдущему примеру изображения поверхности. Каркасное изображение получается путем изображения кривых, получаемых при пересечении этой поверхности плоскостями 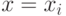и (рис. 6.4).

На самом деле мы будем рисовать четырехугольник и одну диагональ. В процессе рисования нам понадобятся два целочисленных массива: 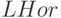(нижний горизонт) и 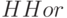(верхний горизонт) размерностью, соответствующей горизонтальному размеру экрана в пикселях. Они нужны для анализа видимости участков изображаемых отрезков. Сначала мы инициализируем верхний горизонт нулем, а нижний - максимальным значением вертикальной координаты на экране. Каждая выводимая на экран точка может закрывать другие точки, которые "скрываются за горизонтом". По мере рисования нижний горизонт "опускается", а верхний "поднимается", постепенно оставляя все меньше незакрытого пространства. В отличие от метода художника, здесь мы продвигаемся от ближнего угла к дальнему. Теперь опишем алгоритм подробнее.

Функция в этом фрагменте предназначена для вывода на экран отрезка прямой, причем в момент инициализации очередного пикселя она выполняет следующие действия:

Таким образом, пиксель выводится только в том случае, если он выше верхнего или ниже нижнего горизонта, после чего его координаты уже сами становятся одним из горизонтов. А в целом алгоритм будет выглядеть так: На рис. 6.5 приведен пример изображения поверхности с использованием этого алгоритма.