Геометрические преобразования

Переход в другую систему координат

Мы рассмотрели преобразования геометрических объектов, заданных в определенной декартовой системе координат. Но во многих случаях удобно рассматривать те же объекты в другой системе координат, поскольку их описание может стать более простым. Самый простой пример - задание координат параллелепипеда: проще всего это сделать в системе координат, совмещенной с одной из его вершин с осями, направленными вдоль ребер. В связи с этим остановимся на вопросе, как изменятся координаты точки при переходе от одной декартовой системы координат к другой.

Рис. 3.9. Две системы координат в пространстве

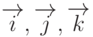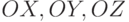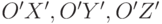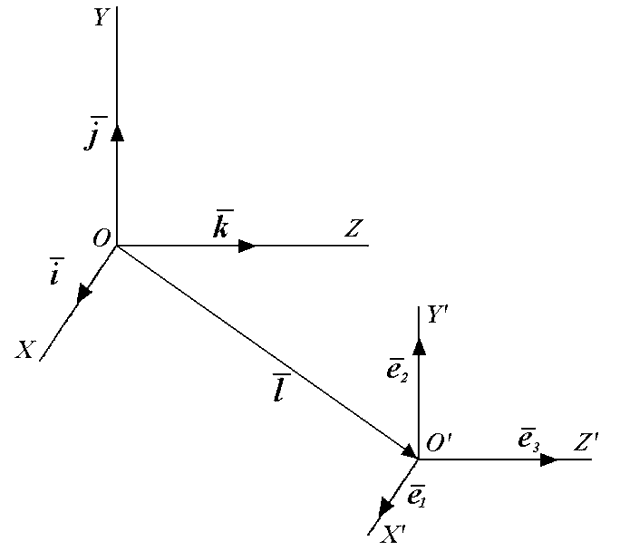
Пусть единичные орты первой системы координат обозначаются , а оси координат - . Введем еще одну систему координат, единичные орты которой обозначим , а оси координат - . Эта система имеет свое начало координат и свои направления осей. Считаем, что в обеих системах координат орты образуют левую тройку (рис. 3.9).

Сначала рассмотрим ситуацию, когда точка 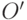совпадает с точкой . Векторы можно задать в первой системе координат, разложив их по векторам :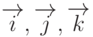

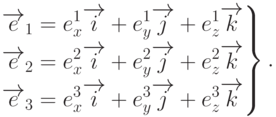
Если в первой системе точка 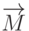имеет координаты 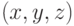, а во второй системе - 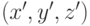, то, очевидно,

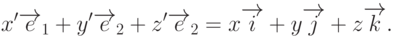
Умножая скалярно это соотношение на векторы , получим связь между значениями координат в разных системах:

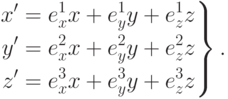
Эти соотношения можно записать в матричном виде

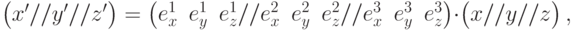( 3.18)

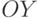Предположим, что вторая система координат получена из первой путем поворота на угол относительно оси . Тогда

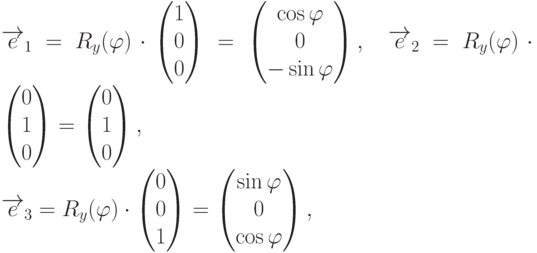
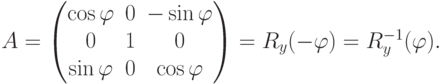
Таким образом, при поворотах системы координат новые координаты точек получаются путем умножения матрицы поворота на противоположный угол на вектор исходных координат.

Если новая система координат получена из старой путем сдвига на вектор 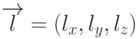, то очевидно, что новые координаты точки задаются формулами

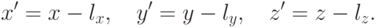
Теперь можно рассмотреть композицию двух преобразований системы координат - переноса и вращения. Тогда координаты точек преобразуются по формуле

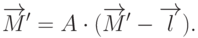( 3.12)