НОУ ИНТУИТ | Комбинаторные алгоритмы для программистов. Лекция 15: Сортировка (часть 2)

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Новосибирский Государственный Университет

Опубликован: 08.11.2006 | Доступ: свободный | Студентов: 1941 / 96 | Оценка: 4.27 / 4.09 | Длительность: 12:16:00

Темы: Программирование, Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 34 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Внешняя сортировка

В методах сортировки, обсуждавшихся в предыдущем разделе, мы полагали, что таблица умещается в быстродействующей внутренней памяти. Хотя для большинства реальных задач обработки данных это предположение слишком сильно, оно, как правило, выполняется для комбинаторных алгоритмов. Сортировка обычно используется только для некоторого сокращения времени работы алгоритмов, в которых сортировка применяется только для некоторого сокращения времени работы алгоритмов, когда оно недопустимо велико даже для задач "умеренных" размеров. Например, часто бывает необходимо сортировать отдельные предметы во времени исчерпывающего поиска ( "Поиск" ), но поскольку такой поиск обычно требует экспоненциального времени, маловероятно, что подлежащая сортировке таблица будет настолько большой, чтобы потребовалось использование запоминающих устройств. Однако задача сортировки таблицы, которая слишком велика для основной памяти, служит хорошей иллюстрацией работы с данными большого объема, и поэтому в этом разделе мы обсудим важные идеи внешней сортировки. Более того, будем рассматривать только сортировку таблицы путем использования вспомогательной памяти с последовательным доступом. Условимся называть эту память лентой.

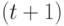Общей стратегией в такой внешней сортировке является использование внутренней памяти для сортировки имен из ленты по частям так, чтобы производить исходные отрезки (известные также как цепочки ) имен в возрастающем порядке. По мере порождения эти отрезки распределяются по рабочим лентам, и затем производится их слияние по отрезков обратно на исходную (t + 1) -ю ленту так, что она будет содержать меньшее число более длинных отрезков. Затем отрезки снова распределяются по остальным лентам, и снова производится их слияние по штук обратно на (t +
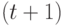1) -ю ленту. Процесс продолжается до тех пор, пока не получится один отрезок, то есть пока таблица не будет полностью отсортирована. Имеются, таким образом, две отдельные проблемы: как порождать исходные отрезки и как осуществлять слияние.

Самый очевидный метод для получения исходных отрезков состоит в том, что можно просто считывать 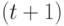(t + 1) -ю ленту имен, рассортировывать их во внутренней памяти и записывать их на ленту в виде отрезка, продолжая процесс до тех пор, пока не будут исчерпаны все имена. Все полученные таким образом исходные отрезки содержат имен (исключая, возможно, последний отрезок). Поскольку число исходных отрезков в конце концов определяет время слияния, мы хотели бы найти некоторый метод образования более длинных исходных отрезков и, следовательно, меньшего их количества. Это можно сделать, используя для сортировки идею турнира (пирамидальную сортировку). При этом подходе имен, которые умещаются в памяти, хранятся в виде такой пирамиды, что сыновья узла больше узла (вместо того, чтобы быть меньше его). Этот метод отвечает определению "победителя" при сравнении имен в сортировках типа турнира как меньшего из двух имен, и это позволяет нам следить за наименьшим именем.

Порождение исходных отрезков продолжается следующим образом. Из входной ленты считываются первые имен, и затем из них формируется пирамида, как описано выше. Наименьшее имя выводится как первое в первом отрезке и заменяется в пирамиде следующим именем из входной ленты в соответствии с алгоритмом 15.2. модифицированным так, чтобы для восстановления пирамиды следить за наименьшим, а не за наибольшим именем. Процесс, известный как выбор с замещением, продолжается таким образом, что к текущему отрезку всегда добавляется наименьшее в пирамиде имя, большее или равное имени, которое последним добавлено к отрезку; при этом добавленное имя заменяется на следующее из входной ленты и восстанавливается пирамида. Когда в пирамиде нет имен, больших, чем последнее имя в текущем отрезке, отрезок обрывается и начинается новый. Этот процесс продолжается до тех пор, пока все имена не сформируются в отрезки.

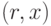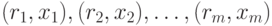Разумный путь реализации этой процедуры состоит в том, чтобы рассматривать каждое имя как пару (r,x) , где есть номер отрезка, в котором находится . Иначе говоря, считается, что пирамида состоит из пар $(r_1,x_1 ),(r_2,x_2 ),\ldots,(r_m,x_m )$ ; сравнения между парами осуществляются лексикографически. Когда считывается имя, меньшее последнего имени в текущем отрезке, оно должно быть в следующем отрезке, и благодаря наличию номера отрезка это имя будет ниже всех имен пирамиды, которые входят в текущий отрезок.

Порождает ли этот выбор с замещением длинные отрезки? Ясно, что он делает это, по крайней мере, не хуже, чем очевидный метод, так как все отрезки (кроме, возможно, последнего) содержат не меньше имен. На самом деле можно показать, что средняя длина отрезков, порождаемых выбором с замещением, равна 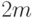, и это вполне можно считать улучшением по сравнению с очевидным методом, в котором средняя длина отрезков равна . Конечно, в лучшем случае все заканчивается только одним исходным отрезком, то есть отсортированной таблицей.

После того, как порождены исходные отрезки, возникает задача повторного распределения их по рабочим лентам и слияния их вместе до тех пор, пока в конце концов мы не получим окончательную отсортированную таблицу. Простейший метод состоит в том, чтобы распределить отрезки по лентам $1,2,\ldots,t$ равномерно и произвести их слияние на ленту t + 1 . Получаемые в результате отрезки снова равномерно распределить по лентам $1,2,\ldots,t$ и снова произвести слияние, образуя более длинные отрезки на ленте t + 1 . Процесс продолжается до тех пор, пока на ленте t + 1 не останется только один отрезок (отсортированная таблица).

Частичная сортировка

Ранее мы изучали проблему полного упорядочения множества имен, не имея a priori информации об абстрактном порядке имен. Имеется два очевидных уточнения этой проблемы. Вместо полного упорядочения требуется только определить -е наибольшее имя (то есть -е имя в порядке убывания) (выбор) или, вместо того чтобы начинать процесс, не располагая информацией о порядке, начинать с двух отсортированных подтаблиц (слияние). Мы рассматриваем обе проблемы частичной сортировки.

Частичная сортировка (выбор)

Как при данных именах $x_1,x_2,\ldots,x_n$ можно найти -е из наибольших в порядке убывания? Задача, очевидно, симметрична: отыскание (n - k + 1) -го наибольшего ( -го наименьшего) имени можно осуществить, используя алгоритм отыскания -го наибольшего, но меняя местами действия, предпринимаемые при результатах < и >сравнения имен. Таким образом, отыскание наибольшего имени (k =
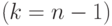1) эквивалентно отысканию наименьшего имени (k = n) ; отыскание второго наибольшего имени (k = 2) эквивалентно отысканию второго наименьшего (k = n - 1) и т.д.

Конечно, все перечисленные варианты задачи выбора можно решить, используя любой из методов полной сортировки имен и затем тривиально обращаясь к -му наибольшему. Такой подход потребует порядка $n\log n$ сравнений имен независимо от значений .

При использовании алгоритма сортировки для выбора наиболее подходящим будет один из алгоритмов, основанных на выборе: либо простая сортировка выбором (алгоритм 15.1) либо пирамидальная сортировка (алгоритм 15.3). В каждом случае мы можем остановиться после того, как выполнены первые шагов. Для простой сортировки выбором это означает использование

$(n - 1) + (n - 2) + \ldots + (n - k) = kn - \frac{{k(k + 1)}}{2}$

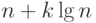сравнений имен, а для пирамидальной — использование $n + k\lg n$ сравнений имен. В обоих случаях мы получаем больше информации, чем нужно, потому что мы полностью определяем порядок

наибольших имен.

Частичная сортировка (слияние)

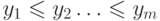Вторым направлением исследования частичной сортировки является задача слияния двух отсортированных таблиц $x_1 \leqslant x_2 \leqslant \ldots \leqslant x_n$ и $y_1 \leqslant y_2 \ldots \leqslant y_m$ в одну отсортированную таблицу $z_1 \leqslant z_2 \leqslant \ldots \leqslant z_{n + m}$ . Существует очевидный способ это сделать: таблицы, подлежащие слиянию, просматривать параллельно, выбирая на каждом шаге меньшее из двух имен и помещая его в окончательную таблицу. Этот процесс немного упрощается добавлением имен-сторожей $x_{n + 1} = y_{m + 1} = \infty$ , как в алгоритме 15.5. В этом алгоритме и указывают, соответственно, на последние имена в двух входных таблицах, которые еще не были помещены в окончательную таблицу.