Что такое граф? Определения и примеры

Остовные деревья

Связный неориентированный ациклический граф называется деревом, множество деревьев называется лесом. В связном неориентированном графе существует по крайней мере один путь между каждой парой вершин; отсутствие циклов в означает, что существует самое большее один такой путь между любой парой вершин в . Поэтому, если - дерево, то между каждой парой вершин в существует в точности один путь. Рассуждение легко обратимо, и поэтому неориентированный граф будет деревом тогда и только тогда, если между каждой парой вершин в существует в точности один путь. Так как наименьшее число ребер, которыми можно соединить вершин, равно и дерево с вершинами содержит в точности ребер, то деревья можно считать минимально связными графами. Удаление из дерева любого ребра превращает его в несвязный граф, разрушая единственный путь между по крайней мере одной парой вершин.

Особый интерес представляют остовные деревья графа , то есть деревья, являющиеся подграфами графа и содержащие все его вершины. Если граф несвязен, то множество, состоящее из остовных деревьев каждой компоненты называется остовном лесом графа. Для построения остовного дерева (леса) данного неориентированного графа , мы последовательно просматриваем ребра , оставляя те, которые не образуют циклов с уже выбранными.

Во взвешенном графе часто интересно определить остовное дерево (лес) с минимальным общим весом ребер, то есть дерево (лес), у которого сумма весов всех его ребер минимальна. Такое дерево называется минимумом оставных деревьев или минимальное остовное дерево. Другими словами, на каждом шаге мы выбираем новое ребро с наименьшим весом (наименьшее ребро), не образующее циклов с уже выбранными ребрами; этот процесс продолжаем до тех пор, пока не будет выбрано ребер, образующих остовное дерево . Этот процесс известен как жадный алгоритм.

Жадный алгоритм может быть выполнен в два этапа. Сначала ребра сортируются по весу и затем строится остовное дерево путем выбора наименьших из имеющихся в распоряжении ребер.

Существует другой метод получения минимума остовных деревьев, который не требует ни сортировки ребер, ни проверки на цикличность на каждом шаге, - так называемый алгоритм ближайшего соседа. Мы начинаем с некоторой произвольной вершины в заданном графе. Пусть - ребро с наименьшим весом, инцидентное ; ребро включается в дерево. Затем среди всех ребер, инцидентных либо , либо , выбираем ребро с наименьшим весом и включаем его в частично построенное дерево. В результате этого в дерево добавляется новая вершина, например, . Повторяя процесс, ищем наименьшее ребро, соединяющее , или с некоторой другой вершиной графа. Процесс продолжается до тех пор, пока все вершины из не будут включены в дерево, то есть пока дерево не станет остовным.

Наихудшим для этого алгоритма будет случай, когда - полный граф (то есть когда каждая пара вершин в графе соединена ребром); в этом случае для того, чтобы найти ближайшего соседа, на каждом шаге нужно сделать максимальное число сравнений. Чтобы выбрать первое ребро, мы сравниваем веса всех 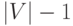ребер, инцидентных вершине , и выбираем наименьшее; этот шаг требует сравнений. Для выбора второго ребра мы ищем наименьшее среди возможных ребер (инцидентных или ) и делаем для этого сравнений. 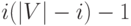Таким образом, ясно, что для выбора -го ребра требуется сравнений, и поэтому в сумме потребуется

Клики

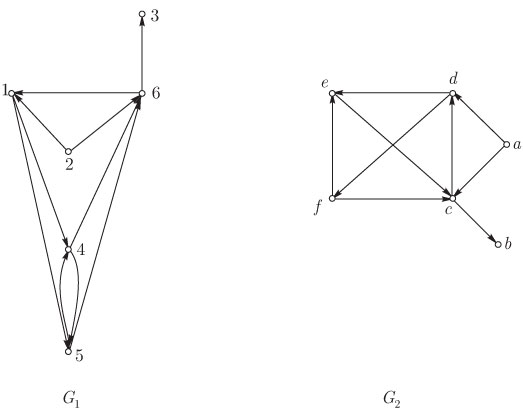
Максимальный полный подграф графа называется кликой графа ; другими словами, клика графа есть подмножество его вершин, такое, что между каждой парой вершин этого подмножества существует ребро и, кроме того, это подмножество не принадлежит никакому большому подмножеству с тем же свойством. Например, на рис. 12.3 показан граф и его клики.

Рис. 12.2. Граф G и все его клики

Клики графа представляют "естественные" группировки вершин, и определение клик графа полезно в кластерном анализе в таких областях, как информационный поиск и социология.

Изоморфизм

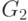Два графа называются изоморфными, если существует взаимно однозначное соответствие , такое, что тогда и только тогда, если , то есть существует соответствие между вершинами графа и вершинами графа , сохраняющее отношение смежности. Например, на рис. 12.3 показаны два изоморфных орграфа: вершины в орграфе соответствуют вершинам 2, 3, 6, 1, 4, 5 в указанном порядке в орграфе 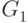. Вообще говоря, между 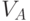и может быть более чем одно соответствие, и на рис. 12.3 графы имеют на самом деле второй изоморфизм: 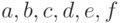соответствуют в указанном порядке вершинам 2, 3, 6, 1, 5, 4. Изоморфные графы отличаются только метками вершин, в связи с чем задача определения изоморфизма возникает в ряде практических ситуаций, таких, как информационный поиск и определение химических соединений.

Заметим, что можно ограничится орграфами. Любой неориентированный граф превращается в орграф заменой каждого ребра двумя противоположно направленными ребрами. Два полученные таким образом орграфа, очевидно, изоморфны тогда и только тогда, если изоморфны исходные графы.

Рис. 12.3. Изоморфные орграфы

Планарность

Граф называют планарным, если существует такое изображение на плоскости его вершин и ребер, что:

• каждая вершина изображается отдельной точкой 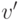на плоскости;
• каждое ребро 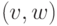изображается простой кривой, имеющей концевые точки ;
• эти кривые пересекаются только в общих концевых точках. Задача определения того, можно ли изобразить граф на плоскости без пересечения ребер, имеет большой практический интерес (например, при конструировании интегральных схем или печатных плат необходимо выяснить, можно ли окончательную схему вложить в плоскость).

Определение планарности графа отличается от других рассмотренных нами задач, поскольку при изображении точек и линий на плоскости приходится больше иметь дело с непрерывными, а не с дискретными величинами. Взаимосвязь между дискретными и непрерывными аспектами планарности заинтересовала математиков и привела к различным характеристикам планарных графов. С точки зрения математики эти характеристики изящны, но эффективных алгоритмов определения планарности они не дают. Наиболее успешный подход к определению планарности состоит просто в том, что граф разбивается на подграфы и затем делается попытка разместить его на плоскости, добавляя подграфы один за другим и сохраняя при размещении планарность.

Вначале сделаем несколько простых, но полезных наблюдений. Поскольку орграф планарен тогда и только тогда, если планарен соответствующий неориентированный граф, полученный игнорированием направления ребер, то достаточно рассматривать только неориентированные графы, поскольку неориентированный граф планарен тогда и только тогда, если все его двусвязные компоненты планарны. Поэтому если неориентированный граф является разделимым, мы можем разложить его на двусвязные компоненты и рассматривать их отдельно. Наконец, поскольку параллельные ребра и петли всегда можно добавить к графу или удалить из него без нарушения свойства планарности, нам достаточно рассматривать только простые графы. Поэтому при определении планарности будем предполагать, что граф неориентированный, простой и двусвязный.

Наша основная стратегия состоит прежде всего в том, чтобы в графе найти цикл , разместить на плоскости в виде простой замкнутой кривой, разложить оставшуюся часть на непересекающиеся по ребрам пути и затем попытаться разместить каждый из этих путей либо целиком внутри , либо целиком вне . Если нам удалось разместить так весь граф , то он планарен, в противном случае он непланарен. Трудность этого способа заключается в том, что при размещении путей можно выбирать либо внутренность, либо внешность , и мы должны проконтролировать, чтобы неправильный выбор области размещения на ранней стадии не устранял возможности размещения последующих путей, - это могло бы привести нас к неверному заключению, что планарный граф непланарен.