Комбинаторные вычисления

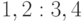Рассмотрим затем, существует ли оптимальное дерево среди тех, у которых в корне не используется монета с номером 0. При таком ограничении в корне дерева можно сделать только два различных сравнения, а именно и . Рассмотрим разбиение исходов по трем ветвям, выходящим из корня, как показано на рис.1.2. Для получения такого, как на рис.1.3, полного двухъярусного тернарного дерева, девять возможных исходов должны были бы быть разбиты в отношении (3, 3, 3). Они же вместо этого разбиваются, соответственно, в отношении (2, 5, 2) и (4,1,4). Таким образом, заключаем, что задачу для четырех монет нельзя решить за два сравнения, не используя дополнительную настоящую монету.

Наконец, рассмотрим те деревья решений, которые используют монету 0 в корне. В этом случае видно, что в корне фактически возможны только два сравнения: 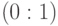и 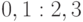. Для первого сравнения набор исходов будет (1, 7, 1), в связи с чем все алгоритмы, начинающиеся таким способом, для нас непригодны. Набор исходов (3, 3, 3) приводит к оптимальному дереву, показанному на рис.1.3. Аналогичным образом устанавливается, что для оптимального дерева сравнения в первом от корня ярусе определяются единственным образом. Отсюда заключаем, что для задачи о четырех монетах фактически существует только одно оптимальное дерево.

Когда используемые идеи анализа задачи о четырех монетах переносятся на произвольный случай, в некоторой степени все идеи обобщаются на случай любого числа монет. Однако некоторые из них не имеют практического значения, когда значительно больше четырех. В принципе, оптимальные деревья решений всегда можно найти путем систематического поиска в множестве деревьев, поскольку для любого заданного в качестве кандидатов требуется рассмотреть лишь конечное число деревьев решений. В лекции обсуждается техника исчерпывающего поиска в таких конечных множествах. Однако, если даже поиск организован разумно и рассматриваются лишь существенно различные (не изоморфные) деревья, эта процедура не может служить практическим способом отыскания оптимальных деревьев решений. С ростом число деревьев растет экспоненциально, и поэтому техника исчерпывающего поиска имеет практическое значение только для малых значений .

Поскольку число листьев в дереве решений должно быть по крайней мере таким же, как и число возможных исходов задачи ( 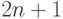для задачи о монетах), сразу же можно получить нижнюю оценку необходимого числа сравнений (или, что эквивалентно, верхнюю оценку числа монет для данного сравнения).

Анализ алгоритмов

В процессе разработки и реализации алгоритма естественным образом раскрываются некоторые его свойства. По мере того как алгоритмы становятся все более и более сложными, все менее и менее вероятно, что их важные свойства проявятся на стадиях разработки и реализации. Как правило, некоторые важные аспекты поведения алгоритма, такие как его корректность, необходимое число операций или объем памяти, определить трудно. Поэтому обычно глубокое понимание нового алгоритма предваряется очень длинной стадией его анализа.

Из-за трудностей анализа им зачастую просто пренебрегают. Вместо этого программа выполняется для того, чтобы увидеть, что получается (например, измеряется время работы). Такой подход можно признать удовлетворительным, если есть основание полагать, что тестовые задачи достаточно хорошо характеризуют работу алгоритма в общем случае; если же это не так, то описанный подход даст мало ценной информации. Даже если тест прекрасно характеризует работу алгоритма, он никогда не даст ответ на придирчивый вопрос, могут ли существовать лучшие алгоритмы для решения той же самой задачи. Проблему оптимальности алгоритма можно решить только путем его анализа.

В анализе алгоритмов существуют две фундаментальные проблемы:

• Какими свойствами обладает данный алгоритм?
• Какие свойства должен иметь любой алгоритм, решающий данную проблему?

Фундаментальная разница между этими двумя вопросами состоит в подходе к ответу на них. В первом случае алгоритм задан и заключения выводятся путем изучения свойств, присущих ему. Во втором случае задается проблема и точно определяется структура алгоритма. Заключения выводятся на основе изучения существа проблемы по отношению к данному классу алгоритмов.

Программа

Программа 1.Поиск фальшивой монеты

//Монета ищется простым перебором.
//Алгоритм реализован на языке программирования Turbo-C++.
#include <stdlib.h>
#include <conio.h>
#include <stdio.h>
int main() {
        clrscr();
        int k, n, flag = -1;
        int *mas;
    printf("Введите число монет: ");
        scanf("%i", &n);
        mas = (int*)malloc(sizeof(n));
        randomize();
        k = random (10) + 1;
        for (int i = 0; i < n; i++) {
                mas[i] = k;
        }
        for (i = k; i == k; i = random (20));
        mas[random (n)] = i;
        printf("Масса монет: ");
        for (i = 0; i < n; i++) {
                printf("%5i", mas[i]);
                if (mas[i] != k) {
                        flag = i;
                }
        }
        printf("\nФальшивая монета под номером %i ее вес %i", flag+1,
mas[flag]);
        getch();
        free(mas);
        return 0;
}