Синхронизирующие эксперименты с линейными автоматами
Из теории автоматов известно, что реакция автомата с памятью непредсказуема, если неизвестно его начальное состояние. Вместе с тем эта реакция может быть предсказана, если имеется информация о том, из какого состояния данный автомат стартовал. Отсюда вполне очевидна важность задачи анализа автоматов, состоящей в распознавании его начального состояния. Другой важной задачей анализа является распознавание конечного (финального) состояния автомата, поскольку знание его позволяет ввести автомат в различные режимы работы, желательные для достижения заданной цели. Напомним, что эксперименты, служащие для определения начального и конечного состояний, принято называть диагностическими и установочными соответственно. Один частный случай установочного эксперимента называется синхронизирующим.
Эта лекция посвящена исследованию некоторых из перечисленных выше экспериментов для линейных автоматов (ЛА). Предварительно мы опишем объект исследования и приведем основные определения, которые потребуются в дальнейшем.
Основные определения
Начнем с краткого описания модели ЛА, а для более детального знакомства с ней отошлем читателя к монографиям [19], [66]. ЛА является системой с конечным числом входных полюсов, к которым подводятся внешние сигналы, и с конечным числом выходных полюсов, на которых наблюдаются сигналы реакции. Воздействия, поступающие на ЛА, прикладываются одновременно ко всем входам в дискретные моменты времени, которые для удобства представляются целыми числами. Интервалы времени между двумя такими последовательными моментами называются тактами.
Структурная схема ЛА состоит из соединения конечного числа элементарных составляющих, каждая из которых мгновенно выполняет одну из трех функций:
- сложение входных сигналов по правилам конечного поля, над которым задан ЛА;
- умножение входного сигнала на константу по правилам конечного поля, над которым задан автомат;
- задержку входного сигнала на один временной такт.
Все операции совершаются одновременно, в результате чего на выходных полюсах ЛА появляются сигналы, принимающие значения из конечного поля, над которым задан ЛА. Таким образом, ЛА может рассматриваться как "черный" ящик с некоторым числом входов и выходов.
Определим три типа компонент, называемых элементарными составляющими ЛА над конечным полем 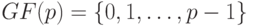 .
.
-
Сумматор. Сумматор имеет
 входов и один выход. Если на входе появились сигналы
входов и один выход. Если на входе появились сигналы 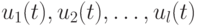 , то на выходе появляется реакция
, то на выходе появляется реакция 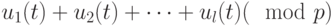 .
. -
Усилитель. Усилитель с константой
 из поля
из поля  имеет один вход и один выход. Если на входе действует сигнал
имеет один вход и один выход. Если на входе действует сигнал  , то на выходе появляется сигнал
, то на выходе появляется сигнал 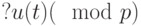 .
. -
Задержка. Задержка имеет один вход и один выход. Если входной сигнал равен
 , то на выходе появляется сигнал
, то на выходе появляется сигнал 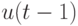 .Сигнал
.Сигнал  обычно называют состоянием задержки в интервале времени от
обычно называют состоянием задержки в интервале времени от  до
до  .
.
При построении ЛА допускается любое соединение конечного числа элементарных составляющих с одним исключением: не должно быть ни одной замкнутой петли, не содержащей по крайней мере одну задержку. Нарушение этого правила приводит к построению соединения, в котором действует неопределенный сигнал.
Отметим, что усилитель с константой 0 или 1 обозначают соответственно разрыв и прямое соединение. Таким образом, ЛА над полем  (двоичный ЛА) состоит только из сумматоров по модулю 2 и задержек. Поэтому практическая привлекательность двоичных ЛА вполне очевидна.
(двоичный ЛА) состоит только из сумматоров по модулю 2 и задержек. Поэтому практическая привлекательность двоичных ЛА вполне очевидна.
Усилитель с константой 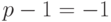 называется инвертором; такой элемент просто изменяет знак входного сигнала.
называется инвертором; такой элемент просто изменяет знак входного сигнала.
Двоичные ЛА являются очень удобными математическими моделями реальных электронных устройств.
Условимся считать, что число входных полюсов ЛА равно  , число выходных полюсов равно
, число выходных полюсов равно  . Предполагается, что входные сигналы принимают значение из поля
. Предполагается, что входные сигналы принимают значение из поля 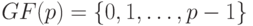 , где
, где  - простое число. Под состоянием ЛА понимается упорядоченная совокупность состояний элементов задержек (обозначим их число через
- простое число. Под состоянием ЛА понимается упорядоченная совокупность состояний элементов задержек (обозначим их число через  ), входящих в состав ЛА. Число
), входящих в состав ЛА. Число  обычно называют размерностью ЛА, и множество состояний обозначают через
обычно называют размерностью ЛА, и множество состояний обозначают через 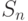 .
.
Введем следующие обозначения:
![\bar u(t)= [u_1(t),\dots , u_l(t)]', \bar y(t)= [y_1(t),\dots, y_m(t)]', \bar s(t)= [s_1(t),\dots, s_n(t)]'.](/sites/default/files/tex_cache/9c2957738b321a6815cd6974fcfe1eb8.png)
Здесь 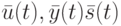 - входной, выходной векторы и вектор-состояние соответственно, а через
- входной, выходной векторы и вектор-состояние соответственно, а через  обозначен момент дискретного времени.
обозначен момент дискретного времени.
Функционирование ЛА  задается системами уравнений состояний и выходов соответственно:
задается системами уравнений состояний и выходов соответственно:
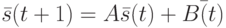 |
( 10.1) |
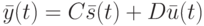 |
( 10.2) |
где ![A=[a_{i,j}]_{nxn}, B=[b_{i,j}]_{nxl}, C=[c_{i,j}]_{mxn}, D=[d_{i,j}]_{mxl}](/sites/default/files/tex_cache/1fcb787ca5b49f780db0c6857d45ae4c.png) , называются характеристическими матрицами ЛА. Матрица
, называются характеристическими матрицами ЛА. Матрица  обычно называется главной (основной) характеристической матрицей. Все перечисленные матрицы состоят из элементов поля
обычно называется главной (основной) характеристической матрицей. Все перечисленные матрицы состоят из элементов поля  .
.
Методом математической индукции можно доказать, что конечное состояние и выходная реакция ЛА  на входное слово
на входное слово 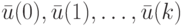 длины
длины  при начальном состоянии
при начальном состоянии  вычисляются по формулам
вычисляются по формулам
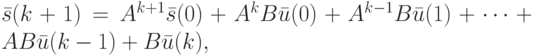 |
( 10.3) |
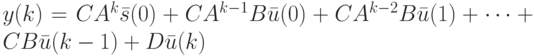 |
( 10.4) |
Последняя из этих формул носит название формулы полной реакции ЛА.
Описанную выше модель принято называть стационарным ЛА. Наряду с ней рассмотрим и так называемые нестационарные ЛА (НЛА), функционирование которых задается следующими уравнениями состояний и выходов соответственно:
 |
( 10.5) |
 |
( 10.6) |
Размерность матриц в этих формулах та же, что и в формулах (10.1) и (10.2).
По аналогии со стационарными ЛА можно доказать, что если 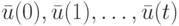 - входная последовательность НЛА и
- входная последовательность НЛА и  - начальное состояние НЛА, то его конечное состояние и выходная реакция вычисляются по следующим формулам:
- начальное состояние НЛА, то его конечное состояние и выходная реакция вычисляются по следующим формулам:
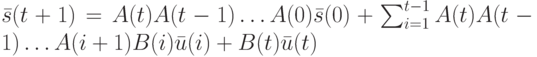 |
( 10.7) |
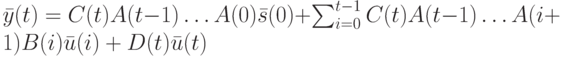 |
( 10.8) |
Определим теперь различные типы экспериментов, которые будут исследоваться нами. Для их проведения необходимо иметь соответствующие последовательности, подаваемые на вход автомата и позволяющие по наблюдаемой реакции находить ответ на интересующий исследователя вопрос. Для разных типов экспериментов необходимо располагать различными типами последовательностей.
Напомним теперь определения соответствующих последовательностей и сделаем это для компактности записей применительно к самой общей модели конечного детерминированного автомата Мили.
Как и ранее, под автоматом Мили понимается пятерка объектов
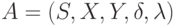
где 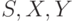 - конечные множества состояний, входной и выходной алфавиты соответственно, а
- конечные множества состояний, входной и выходной алфавиты соответственно, а  и
и  - отображения, называемые функциями переходов и выходов.
- отображения, называемые функциями переходов и выходов.
Пусть 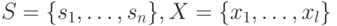 .
.
Определение 10.1. Входная последовательность 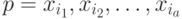 называется синхронизирующее й (СП), если
называется синхронизирующее й (СП), если
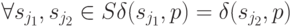
Содержательно это определение означает, что СП  переводит автомат
переводит автомат  в одно и то же конечное состояние независимо от того, из какого состояния он стартовал.
в одно и то же конечное состояние независимо от того, из какого состояния он стартовал.
В этом и приведенных ниже определениях функции переходов и выходов предполагаются расширенными на входные последовательности. Это расширение понимается общепринятым в теории автоматов смысле.
Определение 10.2. Входная последовательность 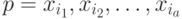 называется установочной (УП), если
называется установочной (УП), если
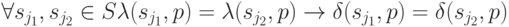
Поясним содержательный смысл этого определения: по наблюдаемой реакции на установочную последовательность однозначно идентифицируется конечное состояние автомата.
Очевидно, что СП можно рассматривать как частный, а точнее, как вырожденный случай УП, поскольку подача СП вызывает перевод автомата в известное конечное состояние, хотя и не требует при этом наблюдения его реакции.
Определение 10.3. Входная последовательность 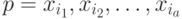 называется диагностической (ДП), если
называется диагностической (ДП), если

Обращаясь к содержательному смыслу этого определения, отметим, что знание реакции автомата на ДП позволяет однозначно идентифицировать его начальное состояние.
Понятно, что каждая ДП одновременно является и УП, поскольку, определив по реакции на ДП начальное состояние автомата, легко определить состояние, в котором он окажется после подачи ДП. Обратное, однако, неверно, т. е. не каждая УП является одновременно и ДП.
Разрешимость установочной и диагностических задач для автомата в общем случае зависит не только от самого автомата, но и от множества начальных состояний, в которых он может находиться перед проведением соответствующего эксперимента. Назовем это множество множеством допустимых начальных состояний автомата  и будем обозначать его через
и будем обозначать его через  . Обычно предполагается, что это множество совпадает со всем множеством
. Обычно предполагается, что это множество совпадает со всем множеством 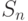 состояний автомата
состояний автомата  . Если это не так, то соответствующий факт будет оговариваться особо.
. Если это не так, то соответствующий факт будет оговариваться особо.
Отметим, что для автоматов Мили, в общем случае нелинейных, в монографии А. Гилла [18] условия существования перечисленных выше последовательностей сформулированы в терминах весьма громоздкой конструкции дерева преемников и потому проверка их является очень трудоемким процессом. Теперь мы перейдем к исследованию условий существования СП для линейных автоматов.
