Гамильтоновы графы
Теорема Дирака
Поиск необходимого и достаточного условия для того, чтобы граф был
гамильтоновым, стал одной из главных нерешенных задач теории графов!
О гамильтоновых графах, в сущности, известно очень мало. Большинство
известных теорем имеет вид "если граф  имеет достаточное
число ребер, то граф
имеет достаточное
число ребер, то граф  является гамильтоновым графом". Вероятно,
самой знаменитой из этих теорем является следующая теорема, принадлежащая
Г.Э.Дираку и потому известная как теорема Дирака.
является гамильтоновым графом". Вероятно,
самой знаменитой из этих теорем является следующая теорема, принадлежащая
Г.Э.Дираку и потому известная как теорема Дирака.
Теорема (Дирак, 1952)
Если в простом графе с  вершинами
вершинами 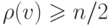 для любой
вершины
для любой
вершины  , то граф
, то граф  является гамильтоновым.
является гамильтоновым.
Замечание Существует несколько доказательств этой широко известной теоремы, здесь мы приводим доказательство Д.Дж.Ньюмана.
Доказательство Добавим к нашему графу  новых вершин, соединяя каждую
из них с каждой вершиной из
новых вершин, соединяя каждую
из них с каждой вершиной из  . Будем предполагать, что
. Будем предполагать, что  — наименьшее число вершин, необходимых для того, чтобы полученный граф
— наименьшее число вершин, необходимых для того, чтобы полученный граф 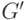 стал
гамильтоновым. Затем, считая, что
стал
гамильтоновым. Затем, считая, что  , придем к противоречию.
, придем к противоречию.
Пусть 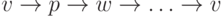 гамильтонов цикл в
графе
гамильтонов цикл в
графе 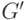 ,
где
,
где 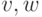 — вершины из
— вершины из  , а
, а  — одна из новых вершин. Тогда
— одна из новых вершин. Тогда  не является смежной с
не является смежной с  , так как в противном случае мы могли бы не
использовать вершину
, так как в противном случае мы могли бы не
использовать вершину  , что противоречит
минимальности
, что противоречит
минимальности  . Более того,
вершина, скажем,
. Более того,
вершина, скажем, 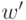 , смежная вершине
, смежная вершине  , не может
непосредственно следовать за вершиной
, не может
непосредственно следовать за вершиной 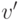 , смежной вершине
, смежной вершине  , потому
что тогда мы могли бы заменить
, потому
что тогда мы могли бы заменить 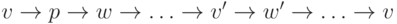 на
на 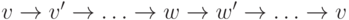 ,
перевернув часть цикла, заключенную между
,
перевернув часть цикла, заключенную между  и
и 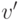 .
Отсюда следует, что число вершин графа
.
Отсюда следует, что число вершин графа 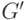 , не являющихся смежными
с
, не являющихся смежными
с  , не меньше
числа вершин, смежных с
, не меньше
числа вершин, смежных с  (то есть равно, по меньшей
мере,
(то есть равно, по меньшей
мере, 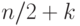 ); с
другой стороны, очевидно, что число вершин графа
); с
другой стороны, очевидно, что число вершин графа 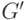 , смежных
с
, смежных
с  , тоже равно, по меньшей мере,
, тоже равно, по меньшей мере, 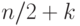 . А так как ни одна вершина
графа
. А так как ни одна вершина
графа 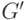 не может быть одновременно смежной и не смежной
вершине
не может быть одновременно смежной и не смежной
вершине  , то общее число вершин графа
, то общее число вершин графа 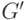 , равное
, равное  , не
меньше, чем
, не
меньше, чем 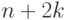 . Это и есть искомое противоречие.
. Это и есть искомое противоречие.
