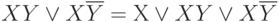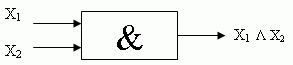Логические основы
Конъюнкция
Возьмем 2 высказывания:
А=<Москва – столица РФ> В=<дважды два - четыре>
тогда сложное высказывание: А & В будет истинным, так как истинны оба этих высказывания.
Поскольку таблица истинности для конъюнкции совпадает с таблицей умножения, если истинному высказыванию приписать значение ' 1 ', а ложному - ' 0 ', то сложное высказывание можно назвать произведением.
Функция конъюнкции истинна тогда, когда истинны одновременно оба высказывания.
Дизъюнкция
Это сложное высказывание истинно тогда, когда истинно хотя бы одно высказывание, входящее в него.
Читается X1 ИЛИ X2: Некоторое отличие от смысла союза "или", принятого в русском языке: в данном случае этот союз употребляется в смысле объединения, а не разъединения.
Логическая равнозначность
Это сложное высказывание истинно тогда, когда истинны или ложны одновременно оба высказывания.
Отсюда следует, что вне зависимости от смысла, равнозначными являются как истинные, так и ложные высказывания.
Например,
А=<дважды два - пять> B=<один плюс два - шесть> А~В равнозначны.
Импликация
Это сложное высказывание ложно только тогда, когда X1 – истинно, а X2 – ложно.
Читается: если X1, то X2. При этом X1 – посылка, X2 – следствие.
Если посмотреть на таблицу истинности, то может показаться странным название этой функции, т.к. из него следует, что истинным может быть высказывание, составленное из двух ложных.
Но в действительности, все верно, т.к. содержанием высказываний в алгебре логики не интересуются.
Тогда из ложной посылки может следовать ложное следствие и это можно считать верным:
<если Киев – столица Франции>, то <2-квадрат 3>.
Эквивалентности
В некоторых случаях сложное и длинное высказывание можно записать более коротким и простым без нарушения истинности исходного высказывания. Это можно выполнить с использованием некоторых эквивалентных соотношений.
Дизъюнкция:
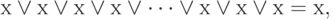
т.е. истинность высказывания не изменится, если его заменить более коротким, таким образом, это правило приведения подобных членов:
x v x = 1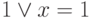
– постоянно истинное высказывание.


- (переместительный) коммуникативный закон.
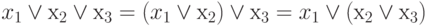
- сочетательный закон.
Конъюнкция:
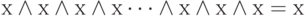
правило приведения подобных членов:
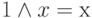
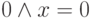 - постоянно ложное высказывание
- постоянно ложное высказывание
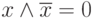 - постоянно ложное высказывание
- постоянно ложное высказывание
Сложение по mod 2
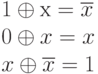
 – при нечетном числе членов, 0 - при четном числе членов
– при нечетном числе членов, 0 - при четном числе членов
Правило де Моргана
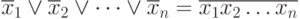
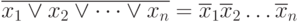
Докажем для двух переменных с помощью таблицы истинности:
Операция поглощения:
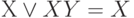 или в общем виде
или в общем виде 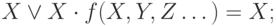
Операция полного склеивания:
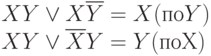
Операция неполного склеивания: