|
Так это же динамическое программирование на основе математической индукции. |
Задача ГП с ограничениями
Двойственная задача
Как и в случае задачи ГП без ограничений, задаче ГП с ограничениями можно сопоставить двойственную задачу. При некоторых предположениях о свойствах прямой и двойственных задач оптимальные значения их целевых функций равны. Это дает возможность получить решение прямой задачи, решив двойственную задачу.
Двойственная задача к задаче GP (задача DGP ) имеет вид:
 |
( 65) |
при ограничениях:
![l_{k}(w) = \sum\limits_{i\in [k]}w_{i},\quad k=\overline{0,p},](/sites/default/files/tex_cache/69dcf2ab5d83f9a2d1a44bbc1a87f412.png) |
( 66) |
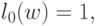 |
( 67) |
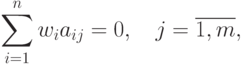 |
( 68) |

Ограничение (67) называется условием
нормальности, ограничения (68) - условиями
ортогональности. Для функции 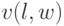 полагаем, что
полагаем, что 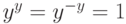 для
для  .
.
Пример 34 Запишем двойственную задачу для задачи ГП из примера 31.
Определим двойственную функцию (65) для задачи ГП. Поскольку в задаче
пять мономов, следовательно, двойственная функция имеет пять
переменных. Вектор коэффициентов задачи 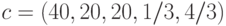 ,
, 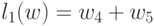 .
Следовательно, двойственная функция для задачи ГП имеет вид:
.
Следовательно, двойственная функция для задачи ГП имеет вид:
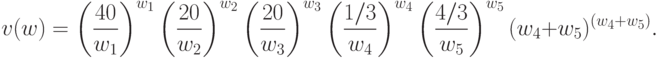
Запишем теперь условия ортогональности (68). Поскольку в прямую задачу
входят три переменные 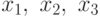 , то условия
ортогональности состоят из трех равенств. В каждом равенстве пять
слагаемых, поскольку в задаче пять мономов. Матрица экспонент
задчи
, то условия
ортогональности состоят из трех равенств. В каждом равенстве пять
слагаемых, поскольку в задаче пять мономов. Матрица экспонент
задчи
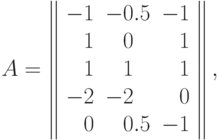
где  -й столбец образован показателями степеней при
-й столбец образован показателями степеней при  -й
переменной
-й
переменной  . По формуле (68)
условия ортогональности для задачи ГП имеют вид:
. По формуле (68)
условия ортогональности для задачи ГП имеют вид:

Запишем условие нормальности. Поскольку позином 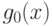 состоит
из трех мономов,
то в условие нормальности входят три слагаемых. Согласно формуле
(67) условие нормальности имеет вид:
состоит
из трех мономов,
то в условие нормальности входят три слагаемых. Согласно формуле
(67) условие нормальности имеет вид:

Таким образом, двойственная задача имеет вид:
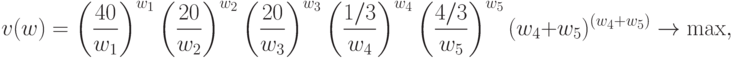
при ограничениях
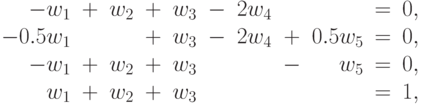
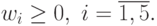
Прежде чем показать, как связаны между собой решения задач GP и DGP, введем следующие определения.
Задача GP называется совместной, если существует по
крайней мере один положительный вектор  , удовлетворяющий ее
ограничениям.
, удовлетворяющий ее
ограничениям.
Задача DGP называется совместной, если существует по
крайней мере один неотрицательный вектор  , удовлетворяющий ее
ограничениям.
, удовлетворяющий ее
ограничениям.
Методы решения для задачи ГП с ограничениями базируются на теоремах, отражающих связь между прямой и двойственной задачами. Приведем формулировки двух основных теорем. Их доказательства можно найти, например, в [5].
Теорема 9 Если пара векторов 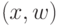 являются допустимыми решениями задач GP и DGP соответственно, то выполняется неравенство
являются допустимыми решениями задач GP и DGP соответственно, то выполняется неравенство
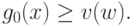
Равенство

достигается тогда и только тогда, когда выполняются следующие условия:
![g_{0}(x) w_{i}= c_i\prod\limits_{j=1}^{m}{x_j}^{a_{ij}},\
i\in [0],](/sites/default/files/tex_cache/b580867bff8393c01ac11b937410b2f0.png)
![w_{i}=l_{k}(w) c_i\prod\limits_{j=1}^{m}{x_j}^{a_{ij}},\ i\in
[k],\ k=\overline{1,p}.](/sites/default/files/tex_cache/60cbbb2c20033a83744aa4e70a0d433d.png)
В следующей теореме сформулированы достаточные условия существования оптимального решения задачи GP.
Теорема 10 Если задача GP совместна и существует допустимое решение  двойственной задачи DGP,
то существует вектор
двойственной задачи DGP,
то существует вектор 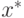 , который является оптимальным решением
задачи GP.
, который является оптимальным решением
задачи GP.
Связь между ГП и выпуклым программированием
Прежде чем показать, какая связь существует между ГП и выпуклым программированием, напомним определения выпуклого множества, выпуклой функции и задачи выпуклого программирования.
Множество точек 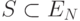 называется выпуклым, если для
любых двух точек
называется выпуклым, если для
любых двух точек  и
и  из
из 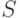 соединяющий их отрезок
соединяющий их отрезок 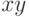 содержится в
содержится в 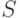 .
.
Функция  , определенная на выпуклом множестве
, определенная на выпуклом множестве 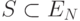 ,
называется выпуклой, если для любых двух точек
,
называется выпуклой, если для любых двух точек  и
и  из
из 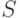 выполняется неравенство
выполняется неравенство
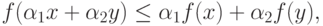
где  ,
,  .
.
Задача выпуклого программирования заключается в минимизации
выпуклой функции  на выпуклом множестве
на выпуклом множестве 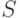 , которое
содержится в области определения функции
, которое
содержится в области определения функции  :
: 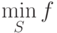 .
.
Одно из важных свойств выпуклого программирования состоит в том, что локальный минимум целевой функции является глобальным минимумом.
Покажем теперь, что при помощи монотонной замены переменных задачу ГП можно заменить эквивалентной задачей выпуклого программирования.
Выполним следующую замену переменных:
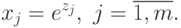
Для записи результатов подстановки мы будем использовать другое
обозначение: 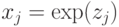 , более удобное, когда степень
экспоненты является сложным выражением. Выполнив замену, получим
положительные показательные функции вида
, более удобное, когда степень
экспоненты является сложным выражением. Выполнив замену, получим
положительные показательные функции вида
![f_k(z)=g_{k}(e^{z_1}, \dots, e^{z_m}) =
\sum\limits_{i\in [k]}c_{i}\exp\left(\sum\limits_{j=1}^{m}a_{ij}z_{j}\right),\ k=\overline{0,p}.](/sites/default/files/tex_cache/d27adc59c09faff88211b0625b80352b.png)
Заметим, что переменные  , тогда как
переменные
, тогда как
переменные 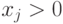 .
.
Таким образом, получим следующую задачу, которую
мы будем называть преобразованная задача 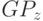 :
:

при ограничениях

где
![f_k(z) =
\sum\limits_{i\in[k]}c_{i}\exp\left(\sum\limits_{j=1}^{m}a_{ij}z_{j}\right),
\ k=\overline{0,p},\ c_i>0,\ a_{ij}\in \mathbb{R},\
z_j\in\mathbb{R}.](/sites/default/files/tex_cache/b0bab07d82a2b1f21d96bbe4e965ee5f.png)
Пример 35 Запишем ГП из примера 31 в виде преобразованной задачи ГП.
Вектор коэффициентов целевой функции 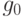 равен
равен
![c_{[0]} = (40, 20, 20),](/sites/default/files/tex_cache/38b119157b0bbdf3b5fe098a01f10702.png)
 равна
равна![A_{[0]}=\left\|
\begin{array}{rlr}
-1 & -0.5 & -1 \\
1 & \phantom{-}0 & 1 \\
1 & \phantom{-}1 & 1
\end{array}
\right\|,](/sites/default/files/tex_cache/09582b5cc2c28495bca2a1833cd1c159.png)
следовательно, преобразованная целевая функция имеет вид

Вектор коэффициентов ограничения 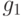 равен
равен
![c_{[1]} = (1/3, 4/3),](/sites/default/files/tex_cache/ea8bc9719efbf5bd55b4419fad06d8ec.png)
матрица экспонент ограничения 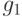 равна
равна
![A_{[1]}=\left\|
\begin{array}{rlr}
-2 & -2 & 0 \\
0 & \phantom{-}0.5 & -1
\end{array}
\right\|,](/sites/default/files/tex_cache/12ac462103358957d0abea6c72f2bcc2.png)
следовательно, преобразованное ограничение имеет вид
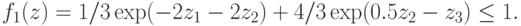
Таким образом, преобразованная задача имеет вид:

при ограничении
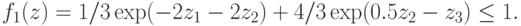
Сформулируем основное свойство преобразованной задачи  в
виде теоремы, доказательство которой можно найти, например, в
[5].
в
виде теоремы, доказательство которой можно найти, например, в
[5].
Теорема 11 Преобразованная задача  является выпуклой задачей. Все
положительные показательные функции
является выпуклой задачей. Все
положительные показательные функции 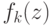 выпуклы.
выпуклы.
Из теоремы следует, что для решения задач ГП можно использовать
методы, разработанные специально для решения задач выпуклого
программирования, предварительно преобразовав задачу ГП в задачу
вида 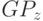 .
.
