Обработка исключений
Самостоятельная работа
Теоретический материал
Вычисление конечных сумм и произведений
Решение многих задач связано с нахождением суммы или произведения элементов заданной последовательности. В данном разделе мы рассмотрим основные приемы вычисления конечных сумм и произведений.
Пусть  - произвольная последовательность n функций. Будем рассматривать конечную сумму вида
- произвольная последовательность n функций. Будем рассматривать конечную сумму вида  . Такую сумму можно записать более компактно, используя следующее обозначение:
. Такую сумму можно записать более компактно, используя следующее обозначение: 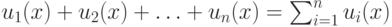 . При
. При  значение суммы равно 0.
значение суммы равно 0.
В дальнейшем будем также использовать сокращенную запись для конечного произведения данной последовательности, которая выглядит следующим образом:  .
.
- Написать программу, которая подсчитывает сумму натуральных чисел от
 до
до  (
(  ).Указания по решению задачи. Пусть
).Указания по решению задачи. Пусть - сумма натуральных чисел от
- сумма натуральных чисел от  до
до  . Тогда
. Тогда 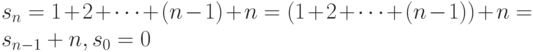 . Мы пришли к рекуррентному соотношению
. Мы пришли к рекуррентному соотношению  , которым мы можем воспользоваться для подсчета суммы. Соотношение
, которым мы можем воспользоваться для подсчета суммы. Соотношение  говорит о том, что сумма на
говорит о том, что сумма на  -ном шаге равна сумме, полученной на предыдущем шаге, плюс очередное слагаемое.
-ном шаге равна сумме, полученной на предыдущем шаге, плюс очередное слагаемое.static void Main() { Console.Write("Ввведите значение n: "); int n=int.Parse(Console.ReadLine()); int s=0; for (int i=1; i<=n; ++i) s+=i; Console.WriteLine("s="+s); } - Написать программу, которая подсчитывает
 ! для вещественного
! для вещественного  и натурального
и натурального  .Указание по решению задачи. Из свойства факториала
.Указание по решению задачи. Из свойства факториала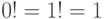 ,
,  ,
,  . Следовательно, факториал можно вычислять, используя рекуррентное соотношение
. Следовательно, факториал можно вычислять, используя рекуррентное соотношение  .
.static void Main() { Console.Write("Ввведите значение n: "); int n=int.Parse(Console.ReadLine()); int f=1; for (int i=1; i<=n; ++i) f*=i; Console.WriteLine("{0}!={1}", n, f); } - Написать программу для подсчета суммы
 , где
, где  - вещественное число,
- вещественное число,  - натуральное число.Указания по решению задачи. Если пронумеровать слагаемые, начиная с
- натуральное число.Указания по решению задачи. Если пронумеровать слагаемые, начиная с , то мы увидим, что номер слагаемого совпадает со значением знаменателя. Рассмотрим каждый числитель отдельно:
, то мы увидим, что номер слагаемого совпадает со значением знаменателя. Рассмотрим каждый числитель отдельно:  Эту последовательность можно представить рекуррентным соотношением
Эту последовательность можно представить рекуррентным соотношением  (1). Теперь сумму можно представить следующим образом,
(1). Теперь сумму можно представить следующим образом,  , а для нее справедливо рекуррентное соотношение
, а для нее справедливо рекуррентное соотношение  ,
,  (2). При составлении программы будем использовать формулы (1-2).
(2). При составлении программы будем использовать формулы (1-2).static void Main() { Console.Write("Ввведите значение n: "); int n=int.Parse(Console.ReadLine()); Console.Write("Ввведите значение x: "); double x=double.Parse(Console.ReadLine()); double b=0, s=0; for (int i=1; i<=n; ++i) { b+=Math.Cos(i*x); s+=b/i; } Console.WriteLine("s={0:f2}",s); } - Написать программу для подсчета суммы
 , где
, где  - вещественное число,
- вещественное число,  - натуральное число.Указания по решению задачи.Перейдем от сокращенной формы записи к развернутой, получимКаждое слагаемое формируется по формуле
- натуральное число.Указания по решению задачи.Перейдем от сокращенной формы записи к развернутой, получимКаждое слагаемое формируется по формуле
 . Если в эту формулу подставить
. Если в эту формулу подставить 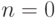 , то получим
, то получим  .
.Чтобы не вводить несколько рекуррентных соотношений (отдельно для числителя, отдельно для знаменателя), представим общий член последовательности слагаемых с помощью рекуррентного соотношением вида
 , где
, где  для нас пока не известно. Найти его можно из выражения
для нас пока не известно. Найти его можно из выражения  . Произведя необходимые расчеты, получим, что
. Произведя необходимые расчеты, получим, что  . Следовательно, для последовательности слагаемых мы получили рекуррентное соотношение
. Следовательно, для последовательности слагаемых мы получили рекуррентное соотношение  ,
,  (3). А всю сумму, по аналогии с предыдущими примерами, можно представить рекуррентным соотношением:
(3). А всю сумму, по аналогии с предыдущими примерами, можно представить рекуррентным соотношением:  ,
,  (4). Таким образом, при составлении программы будем пользоваться формулами (3-4).
(4). Таким образом, при составлении программы будем пользоваться формулами (3-4).using System; namespace Hello { class Program { static void Main() { Console.Write("Ввведите значение n: "); int n=int.Parse(Console.ReadLine()); Console.Write("Ввведите значение x: "); double x=double.Parse(Console.ReadLine()); double a=-1, s=0; for (int i=1; i<=n; ++i) { a*=-x/i; s+=a; } Console.WriteLine("s={0:f2}",s); } } }
Вычисление бесконечных сумм
Будем теперь рассматривать бесконечную сумму вида 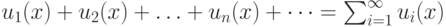 . Это выражение называется функциональным рядом. При различных значениях
. Это выражение называется функциональным рядом. При различных значениях 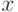 из функционального ряда получаются различные числовые ряды
из функционального ряда получаются различные числовые ряды  . Числовой ряд может быть сходящимся или расходящимся. Совокупность значений
. Числовой ряд может быть сходящимся или расходящимся. Совокупность значений  , при которой функциональный ряд сходится, называется его областью сходимости.
, при которой функциональный ряд сходится, называется его областью сходимости.
Числовой ряд называется сходящимся, если сумма n первых его членов  при
при 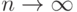 имеет предел, в противном случае, ряд называется расходящимся. Ряд может сходиться лишь при условии, что общий член ряда
имеет предел, в противном случае, ряд называется расходящимся. Ряд может сходиться лишь при условии, что общий член ряда 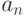 при неограниченном увеличении его номера стремится к нулю:
при неограниченном увеличении его номера стремится к нулю:  . Это необходимый признак сходимости для всякого ряда.
. Это необходимый признак сходимости для всякого ряда.
В случае бесконечной суммы будем вычислять ее с заданной точностью  . Cчитается, что требуемая точность достигается, если вычислена сумма нескольких первых слагаемых и очередное слагаемое оказалось по модулю меньше чем е, то есть это слагаемое на результат практически не влияет. Тогда его и все последующие слагаемые можно не учитывать.
. Cчитается, что требуемая точность достигается, если вычислена сумма нескольких первых слагаемых и очередное слагаемое оказалось по модулю меньше чем е, то есть это слагаемое на результат практически не влияет. Тогда его и все последующие слагаемые можно не учитывать.
Пример. Написать программу для подсчета суммы 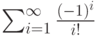 с заданной точностью
с заданной точностью  (
( 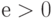 ).
).
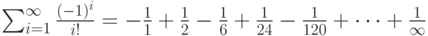 . Как видим, общий член ряда с увеличением значения i стремится к нулю. Поэтому данную сумму можно вычислить, но только с определенной точностью
. Как видим, общий член ряда с увеличением значения i стремится к нулю. Поэтому данную сумму можно вычислить, но только с определенной точностью  . Заметим также, что последовательность слагаемых можно выразить с помощью рекуррентного соотношения
. Заметим также, что последовательность слагаемых можно выразить с помощью рекуррентного соотношения  ,
,  , а всю сумму - с помощью рекуррентного соотношения
, а всю сумму - с помощью рекуррентного соотношения  . (Данные рекуррентные соотношения выведите самостоятельно.)
. (Данные рекуррентные соотношения выведите самостоятельно.)using System;
namespace Hello
{
class Program
{
static void Main()
{
Console.Write("Задайте точность вычислений е: ");
double e=double.Parse(Console.ReadLine());
double a=-1, s=0;
for (int i=2; Math.Abs(a)>=e; ++i)
{
s+=a;
a/=-i;
}
Console.WriteLine("s={0:f2}",s);
}
}
}Практическое задание
- Для заданного натурального
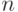 и действительного
и действительного  подсчитать следующие суммы:
подсчитать следующие суммы:-
 ;
; -
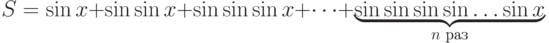 ;
; -
 !;
!; 
-
- Для заданного натурального
 и действительного
и действительного 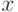 подсчитать следующие выражения:
подсчитать следующие выражения: -
- Вычислить бесконечную сумму ряда с заданной точностью е (e>0).
-
- Вычислить и вывести на экран значение функции
 на отрезке
на отрезке ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) c шагом
c шагом  с точностью
с точностью  .Результат работы программы представить в виде следующей таблицы:
.Результат работы программы представить в виде следующей таблицы:






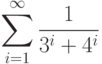


![F(x) = 1+\frac{x^2}{4}+\frac{x^3}{4^2}+\frac{x^4}{4^3}+\frac{x^5}{4^4}+…, x\in [0,1;0,9]](/sites/default/files/tex_cache/aa681c00b99c15c7cccc966e60415cba.png)
![F(x) = 1+\frac{x^3}{3\cdot 2}+\frac{x^5}{5\cdot 2^2}+\frac{x^7}{7\cdot 2^3}…, x\in [0,1;0,99]](/sites/default/files/tex_cache/4a22b04bdbe577c5d500e151af4dd29c.png)
![F(x) = 1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+ \frac{x^8}{9!}…, x\in [0;1]](/sites/default/files/tex_cache/75536966d8f3f77eb7989f08de1c2ded.png)
![F(x) = \frac{x-1}{x}+\frac{(x-1)^2}{2x^2}+\frac{(x-1)^3}{3x^3}+…, x\in [1;2]](/sites/default/files/tex_cache/7f3ce6b93632fe466073711593e51080.png)