Академия Intel:

Введение в программирование больших вычислительных задач на современном Фортране с использованием компиляторов Intel
[+]
Томский государственный университет систем управления и радиоэлектроники
Опубликован: 01.11.2012 | Доступ: свободный | Студентов: 651 / 76 | Длительность: 06:01:00
Тема: Программирование
Специальности: Системный архитектор, Тестировщик
Теги: Intel Parallel Studio, Intel Visual Fortran, fortran, разработка приложений, системы программирования
Лекция 4:

Массивы
A
|
версия для печати
< Лекция 3 || Лекция 4: 1234 || Лекция 5 >

Задание

Методом конечных разностей решить уравнение Лапласа в прямоугольной области.

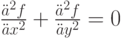
\frac {\ddot a^2f} {\ddot ax^2} + \frac {\ddot a^2f} {\ddot ay^2} = 0

f(x,y)=e^y \cdot \sin(x)Точное решение

Условия на границах.

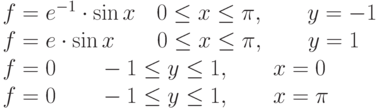
f=e^{-1} \cdot \sin x \quad 0 \leq x \leq \pi, \qquad y=-1 \\ f=e \cdot \sin x \qquad 0 \leq x \leq \pi, \qquad y=1 \\ f=0 \qquad -1 \leq y \leq 1, \qquad x=0 \\ f=0 \qquad -1 \leq y \leq 1, \qquad x= \pi

В расчетной программе, кроме внешнего цикла по итерациям, исключить циклы.

использовать сечения массивов и векторные индексы.

Обтекание уступа.

Построим расчетную сетку.


dx= \frac{2 \pi} {Mi-1} \qquad dy= \frac{1-(-1)} {Mj-1}

Аппроксимируем уравнение Лапласа центральными разностями.

\frac {f_{i+1,j}-2f_{i,j}+f_{i-1,j}} {dx^2} + \frac {f_{i,j+1}-2f_{i,j}+f_{i,j-1}} {dy^2} = 0

Систему линейных алгебраических уравнений решаем итерационным методом верхней релаксации.

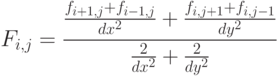
F_{i,j}=\frac { \frac {f_{i+1,j}+f_{i-1,j}}{dx^2} + \frac {f_{i,j+1}+f_{i,j-1}}{dy^2} } { \frac {2}{dx^2} + \frac {2}{dy^2} }

Решение на следующей итерации.

FN_{i,j}=F_{i,j} \cdot relax + (1 - relax) \cdot FN_{i,j} \\ 1 \leq relax < 2 \qquad i=2,Mi-1 \qquad j=2,Mj-1

Условие окончания итерационного процесса.

\sum \limits^{Mi-1}_{i=2} \sum \limits^{Mj-1}_{j=2} \lvert FN_{i,j} - F_{i,j}\rvert < \varepsilon

На стенках заданы условия 1-го рода, протабулируем функции вдоль каждой стенки.

f_{1,j}=0 \qquad j=1,Mj \\ f_{Mi,j}=0 \quad j=1,Mj \\ f_{i,1}=e^{-1} \cdot \sin(x_i) \quad i=1,Mi \\ f_{i,Mj}=e^1 \cdot \sin(x_i) \quad i=1,Mi

Алгоритм решения уравнения Лапласа.


Вариант программы

program  Laplace
integer, parameter :: Mi=40, Mj=40
real(8) :: f(Mi,Mj)=0.0d0, fn, fold
integer iter
real(8), parameter :: eps=1.0d-4
real(8), parameter :: relax=1.5d0
real(8) :: dx, dy, cx=1.0d0

dx=2*acos(0.0)/(Mi-1)
dy=2.0/(Mj-1)

! --- граничные условия
do i=1,Mi
  xt=(i-1)*dx
  f(i,1) =exp(-1.0)*sin(xt)
  f(i,Mj)=exp( 1.0)*sin(xt)
end do

! --- расчет уравнения Лапласа
iter=0
do while(cx>eps)
  iter=iter+1
  cx=0.0d0
  do i=2,Mi-1
  do j=2,Mj-1

    fn=( (f(i+1,j)+f(i-1,j))/(dx*dx) +   &
         (f(i,j+1)+f(i,j-1))/(dy*dy) ) / &
         (2/(dx*dx)+2/(dy*dy))

    fold=f(i,j)
    f(i,j)=relax*fn+(1.0-relax)*f(i,j)
    cx=cx+abs(f(i,j)-fold)

  end do
  end do
end do
  
! --- проверка с точным решением 
cx=0.0d0
do i=1,Mi
  xt=(i-1)*dx
  do j=1,Mj
    yt=(j-1)*dy-1.0
    cx=cx+abs(f(i,j)-exp(yt)*sin(xt))
  end do
end do
write(*,*) "Total = ", cx, " Iterations = ", iter
end

Результат работы программы.

Total =   0.188578398541204
Iterations =          619
Для продолжения нажмите любую клавишу . . .
Дальше >>
< Лекция 3 || Лекция 4: 1234 || Лекция 5 >

Вопросы и ответы

вопросов: 0