Томский государственный университет систем управления и радиоэлектроники
Опубликован: 01.11.2012 | Доступ: свободный | Студентов: 652 / 76 | Длительность: 06:01:00
Тема: Программирование
Специальности: Системный архитектор, Тестировщик
Теги:
Лекция 3:
Управляющие операторы
Вложенные циклы do
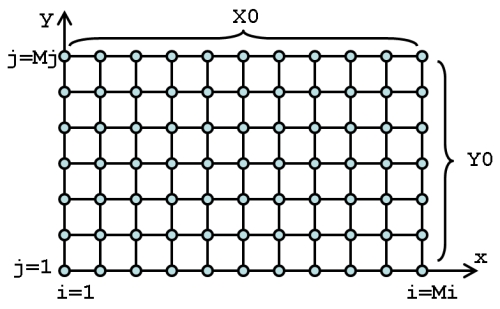
Протабулировать функцию двух переменных
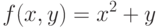
program func_table
integer, parameter :: Mi = 5, Mj = 7 ! сетка
real x, y, fxy, dx, dy
integer i,j
real :: Y0 = 1.0; X0 = 2.0 ! размеры области
dx = X0/(Mj-1); dy = Y0/(Mi-1)
do i = Mi,1,-1 ! сверху вниз
y = (i-1)*dy
do j = 1,Mj
x = (j-1)*dx
fxy = x**2+y
write(*,'(f7.2,\)') fxy
end do
write(*,*); ! переход на следующую строку
end do
end
Управление циклами
Оператор exit – прекращение выполнения цикла.
С1: do k = 1,100 ! внешний цикл с именем С1
do i = 1,200
do j = 1,300
do n = 1,400
if (условие) exit C1
! выход из С1
end do
end do
end do
end do С1
Оператор cycle – прекращение текущей итерации.
Вывести на экран элементы закрашенной области.
Управление циклами
program region
integer :: i,j,s = 0
do i = 1,5
do j = 1,8
s = s+1
if ((i \leq; 3).AND.(j \geq; 5)) cycle ! обход
write(*,"(i4,\)") s
end do
write(*,*)
end do
end
Бесконечные циклы
program region
use iflib
do ! бесконечный вывод псевдослучайных чисел
call random(x)
write(*,"(i1,\)") floor(x*10)
end do
end
do if (логическое условие) exit операторы end do
Цикл выполняющийся хотя бы один раз
do операторы if (логическое условие) exit end do
Псевдослучайные числа
Получить одно псевдослучайное число
call random(x) 0.0 \leq; x < 1.0
Получить одно псевдослучайное число или массив
call random_number(x)
real x integer R call random(x); R = int(x*10) ! [ 0; 9] call random(x); R = int(x*11)-5 ! [-5; 5] call random(x); R = int(x*6)*10 ! 0,10,20,30,40,50
Задания
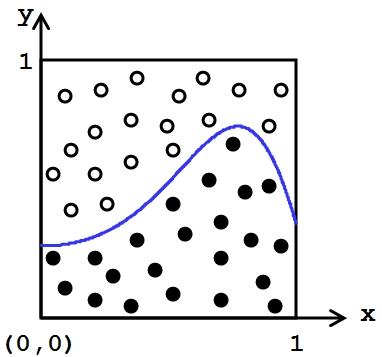
1)Монте-Карло
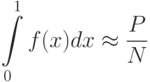
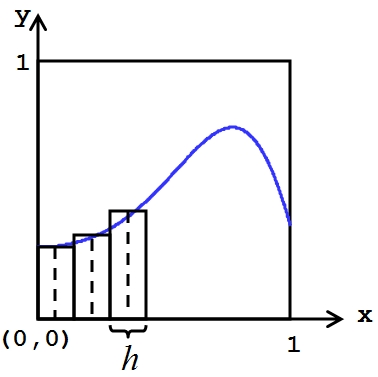
2) средних прямоугольников
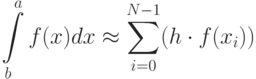
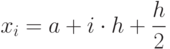

a=0, b=0, N - число отрезков
program Monte_Karlo
integer k ! переменная цикла
real x, y ! случайные координаты точки
integer :: p=0 ! число попаданий
integer :: n=50000 ! число испытаний
real integral ! вычисленное значение интеграла
do k=1,n
call random_number(x)
call random_number(y)
if (y<sin(3*x*x)*exp(x)/4) p=p+1
end do
integral=REAL(p)/REAL(n)
write(*,"(A,f7.3)") "Integral = ", integral
end
Результат работы программы: Integral = 0.244 Для продолжения нажмите любую клавишу . . . |
program Rectangle
integer i ! переменная цикла
real x, a, b ! границы интервала, текущий x
integer :: N=500 ! число прямоугольников
real h ! ширина прямоугольника
real :: integral=0.0 ! вычисленное значение интеграла
a=0
b=1
h=(b-a)/N
do i=0,N-1
x=a+i*h+h/2
integral=integral+h*sin(3*x*x)*exp(x)/4
end do
write(*,"(A,f7.3)") "Integral = ", integral
end
Результат работы программы: Integral = 0.250 Для продолжения нажмите любую клавишу . . . |




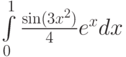 методом:
методом: