Расширенная индексная нотация
Операции сбора/распределения данных
В качестве индекса массива можно использовать сечение массива. Элементы сечения в этом случае определят множество значений индекса.
Примеры:
a[b[0:s]] = c[:] // a[b[0]]=c[0],a[b[1]]=c[1],…
c[0:s] = a[b[:]] // c[0]=a[b[0]],c[1]=a[b[1]],…
Компилятор при использовании таких конструкций генерирует машинный код операций сбора и распределения данных для соответствующей целевой архитектуры.
Пример использования операций распределения/сбора данных:
void fnc1(float *dest, float *src, unsigned int *ind_dest, unsigned int *ind_src, int len) {
dest[ind_dest[0:len]] = src[ind_src[0:len]];
}
#include <iostream>
void foo(float *dest, float *src, unsigned int *ind_dest, unsigned int *ind_src, int len);
int main() {
float x[5] = {1., 2., 3., 4., 5.};
float y[5] = {0., 0., 0., 0., 0.};
unsigned int y_ind[5] = {4,3,2,1,0};
unsigned int x_ind[5] = {1, 3, 0, 2, 4};
std::cout << "x: " << x[:] << " ";
std::cout << std::endl << std::endl;
std::cout << "y: " << y[:] << " ";
std::cout << std::endl << std::endl;
fnc1(y, x, y_ind, x_ind, 5);
std::cout << "y: " << y[:] << " ";
std::cout << std::endl << std::endl;
return(0);
}
Операции линейного/циклического сдвига
Поддерживаются операции линейного и циклического ("ротация") сдвига.
Примеры:
b[:] = __sec_shift(a[:], shift_val, fill_value);
b[:] = __sec_rotate(a[:], shift_val);
Параметр shift_val определяет величину сдвига, а fill_value - значение, которым заполняются "освободившиеся" позиции массива a.
О многомерных массивах
Для работы с сечениями многомерных массивов компилятору необходимо "знать" форму массива.
В C/C++ есть следующие способы описания формы массива:
- массив фиксированного размера:
float a[100][50];
- динамический массив:
typedef int (*a2d)[10]; // указатель на вектор a2d *p; p = (a2d) malloc(sizeof(int)*rows*10); p[5][:] = 42; // задать элементы 5-й строки p[0:rows][:] = 42; // задать все элементы массива p[:][:] = 42; // ошибка (размер строки должен быть задан явно)
Массивы как аргументы
Сечение массива можно использовать в качестве аргумента функции. Фактические и формальные аргументы должны быть согласованы.
Пример:
void saxpy_vec(int m, float a, float restrict x[m], float restrict y[m])
{
y[:] += a * x[:];
}
cilk_for(int i = 0; i < n; i += 256)
saxpy_vec(112, 1.7, &x[i],&y[i]);
Примеры
Модификация подматрицы размером 
, начиная с элемента (i, j):
vx[i:m][j:n] += a*(U[i:m][j+1:n]-U[i:m][j:n]);
Использование элементной функции:
theta[0:n] = atan2(y[0:n],1.0);
Сбор/распределение данных:
w[0:n] = x[i[0:n]];
y[i[0:n]] = z[0:n];
Использование сечения массива в условном операторе (выполняются обе ветви):
if(a[0:n] < b[0:n])
c[0:n] += 1;
else
c[0:n] -= 1;
Умножение полиномов
Умножение полиномов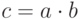 
:
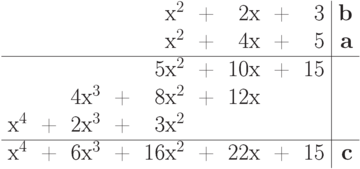
Хранение коэффициентов:
Векторная реализация (сложность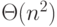 
):
void simple_mul( T c[], const T a[], const T b[], size_t n ) {
c[0:2*n-1] = 0;
for (size_t i=0; i<n; ++i)
c[i:n] += a[i]*b[0:n];
}
Алгоритм Карацубы
Алгоритм Карацубы (сложность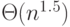 
) – оптимален для n = 32 – 1024
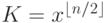
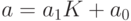
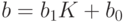
Вычислить:
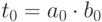
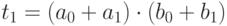
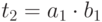
Тогда:
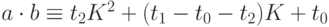
Реализация с помощью сечений:
void karatsuba( T c[], const T a[], const T b[], size_t n ) {
if( n<=CutOff ) {
simple_mul( c, a, b, n );
} else {
size_t m = n/2;
karatsuba( c, a, b, m ); // t0 = a0 x b0
karatsuba( c+2*m, a+m, b+m, n-m ); // t2 = a1 x b1
temp_space<T> s(4*(n-m));
T *a_=s.data(), *b_=a_+(n-m), *t=b_+(n-m);
a_[0:m] = a[0:m]+a[m:m]; // a_ = (a0+a1)
b_[0:m] = b[0:m]+b[m:m]; // b_ = (b0+b1)
karatsuba( t, a_, b_, n-m ); // t1 = (a0+a1) x (b0+b1)
t[0:2*m-1] -= c[0:2*m-1] + c[2*m:2*m-1]; // t = t1-t0-t2
c[2*m-1] = 0;
c[m:2*m-1] += t[0:2*m-1]; // c = t2K2+(t1-t0-t2)K+t0
}
}
Схема распараллеливания:
