|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
F. Теория информации
В этом приложении мы обсуждаем несколько концепций теории информации, которые связаны с темами, рассмотренными в этой книге.
F.1. Измерение информации
Как мы можем измерить информацию в событии? Сколько информации нам доставляет событие? Давайте ответим на эти вопросы с помощью примеров.
Пример F.1
Вообразите человека, сидящего в комнате. Глядя из окна, он может ясно видеть, что сияет солнце. Если в этот момент он получает сообщение (событие) от соседа, который говорит "Хороший день", это сообщение содержит какую-либо информацию? Конечно нет! Человек уже уверен, что это день и погода хорошая. Сообщение не уменьшает неопределенности его знаний.
Пример F.2
Вообразите, что человек купил лотерейный билет. Если друг звонит, чтобы сказать, что он выиграл первый приз, это сообщение (событие) содержит информацию? Конечно да! Сообщение содержит много информации, потому что вероятность выигрыша первого приза является очень маленькой. Приемник сообщения потрясен.
Вышеупомянутые два примера показывают, что есть отношения между полноценностью события и ожиданиями приемника. Если приемник удален от места события, когда событие случается, сообщение содержит много информации; иначе - это не так. Другими словами, информационное содержание сообщения обратно пропорционально связано с вероятностью возникновения этого сообщения. Если событие очень вероятно, оно не содержит никакой информации (Пример F.1); если оно является маловероятным, оно содержит много информации (Пример F.2).
F.2. Энтропия
Предположим, что S - распределение вероятностей конечного числа событий (См. "приложение D" ). Энтропия или неопределенность в S может быть определена как:
![H(S) = \sum P(S) x\ [log_{2}\ 1/p\(s)]\ бит](/sites/default/files/tex_cache/ad10febd67692326154243204d72983e.png)
где 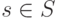 - возможный результат одного испытания. Обратите внимание, что, если. P (s) = 0, то мы будем считать, что P(S) x [log2 1/p(s)] равно 0, чтобы избежать деления на 0.
- возможный результат одного испытания. Обратите внимание, что, если. P (s) = 0, то мы будем считать, что P(S) x [log2 1/p(s)] равно 0, чтобы избежать деления на 0.
Пример F.3
Предположим, что мы бросаем правильную монету. Результаты - "орел" и "решка", каждый с вероятностью 1/2, и это означает
H (S) = P(орел) x [log2 1/ (P (решка)] + P (решка) x [log2 1 / (P (решка)] H (S) = (1/2) x [log2 1 / (1/2) 1 + (1/2) x [log2 1 / (1/2)] = 1 бит
Этот пример показывает, что результат бросания правильной монеты дает нам 1 бит информации (неопределенность). При каждом бросании мы не знаем, каков будет результат, поскольку две возможности одинаково вероятны.
Пример F.4
Предположим, что мы бросаем неправильную (поврежденную) монету. Результаты выпадения "орла" и "решки" следующие P ("орел") = 3/4 и P ("решка") = 1/4. Это означает, что
H (S) = (3/4) x [log2 1 / (3/4)] + (1/4) x [log2 1 / (1/4)] = 0,8 бит
Этот пример показывает, что результат бросания неправильной монеты дает нам только 0,8 битов информации (неопределенность). Количество информации здесь меньше, чем количество информации в Примере F.3, потому что мы ожидаем получить "орлов" большее число раз, чем "решек".
Пример F.5
Теперь предположим, что мы бросаем полностью неправильную монету, в которой результат является всегда "орел", P ("орел") = 1 и P ("решка") = 0. Энтропия в этом случае
H (S) = (1) x [log21)] + (0) x [log2 1 / (0)] = (1) x (0) + (0) = 0
В этом эксперименте нет никакой информации (неопределенности). Мы знаем, что результатом всегда будет "орел" ; энтропия - 0.
Максимальная энтропия
Может быть доказано, что для распределения вероятностей с n возможными результатами максимальная энтропия может быть достигнута, только если все вероятности равны (все результаты одинаково вероятны). В этом случае максимальная энтропия
Hmax = log2n бит
Другими словами, энтропия любого множества вероятностей имеет верхний предел, который определяется этой формулой.
Пример F.6
Предположим, что бросается шестигранная игральная кость. Энтропия испытания равна
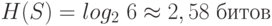
Минимальная энтропия
Можно доказать, что для распределения вероятностей с n возможными результатами, получается минимальная энтропия тогда и только тогда, когда все время получается один из результатов. В этом случае минимальная энтропия
Hmin (S) = 0 битов
Другими словами, эта формула определяет нижний предел энтропии для любого набора вероятностей.
Интерпретация энтропии
Энтропию можно воспринимать как число бит, которым можно представить каждый результат из множества вероятностей, в том случае, когда результаты одинаково вероятны. Например, когда возможное случайное распределение имеет восемь возможных результатов, каждый результат может быть представлен в виде трех бит (от 000 до 111 ). Когда мы получаем результат эксперимента, мы можем сказать, что получили 3 бита информации. Энтропия этого набора вероятностей - также 3 бита ( ln2 8 = 3 ).
Совместная энтропия
Когда мы имеем два набора распределения вероятностей, S1 и S2, мы можем определить совместную энтропию H (S1, S2) как
![H (S_{1}, S_{2}) = \sum \sum P(x,y))\ x \ [log_{2 } \ 1/P \ (x, y)]\ бит](/sites/default/files/tex_cache/47208be251100903ea6ea9d4863d6e51.png)
Условная энтропия
Мы часто должны знать неопределенность распределения вероятностей S1, при условии получения результата, который определяется неопределенностью распределения вероятности S2. Она называется условной энтропией H (S1| S2). Может быть доказано, что
H (S1| S2) = H (S1, S2) - H (S2) бит
Другие соотношения
Приведем здесь без доказательства некоторые другие соотношения для энтропии:
- H (S1, S2) = H (S2 | S1) + H (S1) = H (S1| S2) + H (S2)
- H (S1, S2) <= H (S1) + H (S2)
- H (S1| S2) <= H (S1)
- H (S1, S2, S3) = H (S1| S2, S3) + H (S1, S3)
Второе и третье соотношения справедливы, если S1 и S2 статистически независимы.
Пример F.7
В криптографии, если P - распределение вероятностей исходного текста, C - распределение вероятностей зашифрованного текста и K - распределение вероятностей ключей, то H (K|C) может интерпретироваться как сложность атаки зашифрованного текста, в которой знание C может привести к знанию K.
Пример F.8
В криптографии, учитывая исходный текст и ключ, детерминированный алгоритм шифрования создает уникальный зашифрованный текст, что означает H (C | K, P) = 0 . Также учитывая зашифрованный текст и ключевой алгоритм дешифрования, создается уникальный исходный текст, что означает H (P | K, C) = 0. Если дан зашифрованный текст и исходный текст, ключ также определяется уникально: H (K | P, C) = 0.
Совершенная секретность
В криптографии, если P, K и C - пространства выборки вероятности исходного текста, зашифрованного текста и ключа соответственно, то мы имеем H (P|C) <=H (P). Это может быть интерпретировано так: неопределенность P данного C меньше или равна неопределенности P. В большинстве криптографических систем, справедливо отношение H (P|C)< H (P), что означает, что перехват зашифрованного текста уменьшает знание, которое требуется для того, чтобы найти исходный текст. Криптографическая система обеспечивает совершенную секретность, если соблюдается соотношение H (P|C)=H (P), - это означает, что неопределенность исходного текста и данного зашифрованного текста - одна и та же неопределенность исходного текста. Другими словами, Ева не получает никакой информации, перехватив зашифрованный текст; она по-прежнему должна исследовать все возможные варианты.
Пример F.9
В предыдущих лекциях мы утверждали, что одноразовый шифр блокнота обеспечивает совершенную секретность. Докажем этот факт, используя предыдущие соотношения энтропии. Предположим, что алфавит - только 0 и 1. Если длина сообщения - L, может быть доказано, что ключ и зашифрованный текст состоят из 2L символов, в которых каждый символ является одинаково вероятным. Следовательно, H (K) = H (C) = log22L = L. Используя отношения, полученные в примере F.8, и то, что H (P, K) = H (P) + H (K), потому что P и K независимы, мы имеем
H (P, K, C) = H (C|P, K) + H (P, K) = H (P, K) = H (P) + H (K) H (P, K, C) = H (K|P, C) + H (P, C) = H (P, C) = H (P|C) + H (C)
Это означает, что H (P | C) = H (P)
Пример F.10
Шеннон показал, что в криптографической системе, если (1) ключи возникают с равной вероятностью и (2) для каждого исходного текста и каждого зашифрованного текста есть уникальный ключ, то криптографическая система обеспечивает совершенную секретность. Доказательство использует тот факт, что в этом случае распределения вероятностей ключей, исходного текста и зашифрованного текста имеют один и тот же размер.
F.3. Энтропия языка
Интересно связать концепцию энтропии с естественными языками, такими как английский язык. В этом разделе мы касаемся некоторых пунктов, связанных с энтропией языка.
Энтропия произвольного языка
Предположим, что язык использует N букв и все буквы имеют равную вероятность появления. Мы можем сказать, что энтропия этого языка - HL = log2N. Например, если мы используем двадцать шесть прописных букв (от A до Z), чтобы передать наше сообщение, то энтропия, или информация, содержащаяся в каждой букве, равна HL = log2 26 = 4,7 битов. Другими словами, от каждой буквы мы получаем 4,7 бита информации. Это означает, что мы можем кодировать буквы на этом языке, используя слова по 5 битов; вместо того чтобы посылать букву, мы можем передать одно слово из 5 битов.
Энтропия английского языка
Энтропия английского языка - намного меньше, чем 4,7 бита, по двум причинам (если мы используем только прописные буквы). Первое: буквы возникают с неодинаковой вероятностью.
"Лекция 3"
показывает частоту появления букв в английском языке. Буква E возникнет намного более вероятно, чем буква Z. Второе: существование диграмм (сочетаний по две буквы) и триграмм (сочетаний по три буквы) уменьшает количество информации в полученном тексте. Если мы получаем букву Q, вероятнее всего, что следующая буква - U. Также, если мы получаем пять последовательных букв SELLI, то вероятно, что следующие две буквы будут QG. Эти два факта уменьшают энтропию английского языка. Шеннон показал, что среднее значение энтропии английского языка 1А.Н. Колмогоров в своей статье "Три подхода к определению понятия количества информации
" приводит оценку энтропии русского языка на основе словаря С.И. Ожегова -это 1,9  l0,1 равно 1,50.
l0,1 равно 1,50.
Избыточность
Избыточность языка была определена как R = 1 - HL /(log2N). В случае английского языка, используя только прописные буквы, мы получим R = 1 - 1,50/4,7 = 0,68. Другими словами, в английском сообщении есть 70-процентная избыточность. Алгоритм может сжать английский текст до 70 процентов, не теряя содержания.
Интервал однозначности
Другое определение, введенное Шенноном, - интервал однозначности. Интервал однозначности - минимальная длина зашифрованного текста, n0,которая требуется Еве, чтобы уникально определить ключ (за достаточно большое число повторений) и в конечном счете вычислить исходный текст. Интервал однозначности определен как
n0 = H (K) / [R x H (P)]
Пример F.11
Шифр подстановки использует множество ключей, состоящих из 26 ключей, и алфавит из 26 символов. Используя избыточность 0,70 для английского языка, определяем интервал однозначности:
n0 = (log 2 26!) / (0,70 x log2 26) = 27
Это означает, что зашифрованный текст должен содержать по крайней мере 27 символов, для того чтобы Ева могла уникально найти исходный текст.
Пример F.12
Шифр сдвига использует множество из 26 ключей и алфавит из 26 символов. Используя избыточность 0,70 для английского языка, интервал однозначности определяем следующим соотношением:
n0 = (log 26)/0,70 x log226) = 1,5
Это означает, что Еве необходимо иметь по крайней мере 2 символа зашифрованного текста, чтобы уникально найти исходный текст. Конечно, это весьма приблизительная оценка. В фактической ситуации Ева нуждается в большем количестве символов, чтобы нарушить код.
