Squirrel Eat Squirrel
Collision Detection: Eat or Be Eaten
272. # check if the player has collided with any squirrels 273. for i in range(len(squirrelObjs)-1, -1, -1): 274. sqObj = squirrelObjs[i]
The for loop on 273 will go run code on each of the enemy squirrel game objects in squirrelObjs. Notice that the parameters to range() on line 273 start at the last index of squirrelObjs and decrement. This is because the code inside this for loop may end up deleting some of these enemy squirrel game objects (if the player’s squirrel ends up eating them), so it is important to iterate from the end down to the front. The reason why was explained previously in the "When Deleting Items in a List, Iterate Over the List in Reverse" section.
275. if 'rect' in sqObj and playerObj['rect'].colliderect(sqObj['rect']): 276. # a player/squirrel collision has occurred 277. 278. if sqObj['width'] * sqObj['height'] <= playerObj['size']**2: 279. # player is larger and eats the squirrel 280. playerObj['size'] += int( (sqObj['width'] * sqObj['height'])**0.2 ) + 1 281. del squirrelObjs[i]
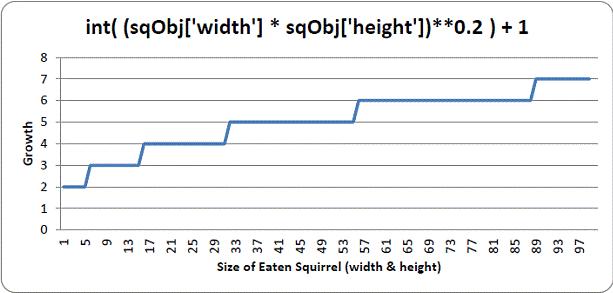
If the player’s squirrel is equal or larger than the size of the enemy squirrel it has collided with, then the player’s squirrel will eat that squirrel and grow. The number that is added to the 'size' key in the player object (that is, the growth) is calculated based on the enemy squirrel’s size on line 280. Here’s a graph showing the growth from different sized squirrels. Notice that larger squirrels cause more growth:
So, according to the chart, eating a squirrel that has a width and height of 45 (that is, an area of 1600 pixels) would cause the player to grow 5 pixels wider and taller.
Line 281 deletes the eaten squirrel object from the squirrelObjs list so that it will no longer appear on the screen or have its position updated.
283. if playerObj['facing'] == LEFT: 284. playerObj['surface'] = pygame.transform.scale(L_SQUIR_IMG, (playerObj['size'], playerObj['size'])) 285. if playerObj['facing'] == RIGHT: 286. playerObj['surface'] = pygame.transform.scale(R_SQUIR_IMG, (playerObj['size'], playerObj['size']))
The player’s squirrel image needs to be updated now that the squirrel is larger. This can be done by passing the original squirrel image in L_SQUIR_IMG or R_SQUIR_IMG to the pygame.transform.scale() function, which will return an enlarged version of the image. Depending on whether playerObj['facing'] is equal to LEFT or RIGHT determines which original squirrel image we pass to the function.
288. if playerObj['size'] > WINSIZE: 289. winMode = True # turn on "win mode"
The way the player wins the game is by getting the squirrel to have a size larger than the integer stored in the WINSIZE constant variable. If this is true, then the winMode variable is set to True. Code in the other parts of this function will handle displaying the congratulations text and checking for the player to press the R key to restart the game.
291. elif not invulnerableMode: 292. # player is smaller and takes damage 293. invulnerableMode = True 294. invulnerableStartTime = time.time() 295. playerObj['health'] -= 1 296. if playerObj['health'] == 0: 297. gameOverMode = True # turn on "game over mode" 298. gameOverStartTime = time.time()
If the player’s area was not equal to or larger than the area of the enemy squirrel, and invulnerableMode was not set to True, then the player will take damage from colliding with this larger squirrel.
To prevent the player from being damaged several times by the same squirrel immediately, we will briefly make the player invulnerable to further squirrel attacks by setting invulnerableMode to True on line 293. Line 294 will set invulnerableStartTime to the current time (which is returned by time.time()) so that lines 133 and 134 can know when to set invulnerableMode to False.
Line 295 decrements the player’s health by 1. Because there is a chance that the player’s health is now at 0, line 296 checks for this and, if so, sets gameOverMode to True and gameOverStartTime to the current time.
The Game Over Screen
99. else: 300. # game is over, show "game over" text 301. DISPLAYSURF.blit(gameOverSurf, gameOverRect) 302. if time.time() - gameOverStartTime < GAMEOVERTIME: 303. return # end the current game
When the player has died, the "Game Over" text (which is on the Surface object in the gameOverSurf variable) will be shown on the screen for the number of seconds that is in the GAMEOVERTIME constant. Once this amount of time has elapsed, then the runGame() function will return.
This lets the enemy squirrels continue to be animated and moving around for a few seconds after the player dies and before the next game starts. The "game over screen" in Squirrel Eat Squirrel does not wait until the player presses a key before a new game starts.
Winning
305. # check if the player has won. 306. if winMode: 307. DISPLAYSURF.blit(winSurf, winRect) 308. DISPLAYSURF.blit(winSurf2, winRect2) 309. 310. pygame.display.update() 311. FPSCLOCK.tick(FPS)
The winMode variable is set to True on line 289 if the player has reached a certain size (which is dictated by the WINSIZE constant). All that happens when the player has won is that the "You have achieved OMEGA SQUIRREL!" text (which is on the Surface object stored in the winSurf variable) and the "(Press "r" to restart.)" text (which is on the Surface object stored in the winSurf2 variable) appears on the screen. The game continues until the user presses the R key, at which point the program execution will return from runGame(). The event handling code for the R key is done on lines 238 and 239.
Drawing a Graphical Health Meter
316. def drawHealthMeter(currentHealth): 317. for i in range(currentHealth): # draw red health bars 318. pygame.draw.rect(DISPLAYSURF, RED, (15, 5 + (10 * MAXHEALTH) - i * 10, 20, 10)) 319. for i in range(MAXHEALTH): # draw the white outlines 320. pygame.draw.rect(DISPLAYSURF, WHITE, (15, 5 + (10 * MAXHEALTH) - i * 10, 20, 10), 1)
To draw the health meter, first the for loop on line 317 draws the filled-in red rectangle for the amount of health the player has. Then the for loop on line 319 draws an unfilled white rectangle for all of the possible health the player could have (which is the integer value stored in the MAXHEALTH constant). Note that the pygame.display.update() function is not called in drawHealthMeter().
The Same Old terminate() Function
323. def terminate(): 324. pygame.quit() 325. sys.exit()
The terminate() function works the same as in the previous game programs.
The Mathematics of the Sine Function
328. def getBounceAmount(currentBounce, bounceRate, bounceHeight): 329. # Returns the number of pixels to offset based on the bounce. 330. # Larger bounceRate means a slower bounce. 331. # Larger bounceHeight means a higher bounce. 332. # currentBounce will always be less than bounceRate 333. return int(math.sin( (math.pi / float(bounceRate)) * currentBounce ) * bounceHeight) 334.
There is a mathematical function (which is similar to functions in programming in that they both "return" or "evaluate" to a number based on their parameters) called sine (pronounced like "sign" and often abbreviated as "sin"). You may have learned about it in math class, but if you haven’t it will be explained here. Python has this mathematic function as a Python function in the math module. You can pass an int or float value to math.sin(), and it will return a float value that is called the "sine value"
In the interactive shell, let’s see what math.sin() returns for some values:
>>> import math >>> math.sin(1) 0.8414709848078965 >>> math.sin(2) 0.90929742682568171 >>> math.sin(3) 0.14112000805986721 >>> math.sin(4) -0.7568024953079282 >>> math.sin(5) -0.95892427466313845
It seems really hard to predict what value math.sin() is going to return based on what value we pass it (which might make you wonder what math.sin() is useful for). But if we graph the sine values of the integers 1 through 10 on a graph, we would get this:
You can kind of see a wavy pattern in the values returned by math.sin(). If you figure out the sine values for more numbers besides integers (for example, 1.5 and 2.5 and so on) and then connect the dots with lines, you can see this wavy pattern more easily:
In fact, if you kept adding more and more data points to this graph, you would see that the sine wave looks like this:
Notice that math.sin(0) returns 0, then gradually increases until math.sin(3.14 / 2) returns 1, then it begins to decrease until math.sin(3.14) returns 0. The number 3.14 is a special number in mathematics called pi (pronounced the same as delicious "pie"). This value is also stored in the constant variable pi in the math module (which is why line 333 uses the variable, math.pi), which is technically the float value 3.1415926535897931. Since we want a wavy-looking bounce for our squirrel, we’ll only pay attention to the return values of math.sin() for the arguments 0 to 3.14:
Let’s take a look at the return value of getBounceAmount() and figure out what it does exactly.
333. return int(math.sin( (math.pi / float(bounceRate)) * currentBounce ) * bounceHeight)
Remember that on line 21 we set the BOUNCERATE constant to 6. This means that our code will only increment playerObj['bounce'] from 0 to 6 and that we want to split up the range of floating-point values from 0 to 3.14 into 6 parts, which we can do with simple division: 3.14 / 6 = 0.5235. Each of the 6 equal parts of the 3.14 length on the graph for the "sine wave bounce" is 0.5235.
You can see that when playerObj['bounce'] is at 3 (halfway between 0 and 6), the value passed to the math.sin() call is math.pi / 6 * 3, which is 1.5707 (halfway between 0 and 3.1415). Then math.sin(1.5707) will return 1.0, which is the highest part of the sine wave (and the highest part of the sine wave happens half way through the wave).
As playerObj['bounce'] gets its value incremented, the getBounceAmount() function will return values that have the same bounce shape that the sine wave has from 0 to 3.14. If you want to make the bounce higher, than increase the BOUNCEHEIGHT constant. If you want to make the bounce slower, than increase the BOUNCERATE constant.
The sine function is a concept from trigonometry mathematics. If you’d like to learn more about the sine wave, the Wikipedia page has detailed information: http://en.wikipedia.org/wiki/Sine