|
Добрый день! Подскажите пжл, не разобралась, обучение все платное? Мне сказали бесплатное есть... |
Рынок капитала
12.2. Рынок основного капитала
12.2.1. Дисконтирование
Организация нового производства невозможна без капиталовложений в сооружения, здания и оборудование. Дальнейшая работа предприятия также требует затрат, связанных с обновлением и восстановлением действующего основного капитала.
Фактор времени
Основной капитал является производственным фактором длительного пользования: его участие в хозяйственной деятельности фирмы продолжается в течение нескольких лет, а то и десятилетий с момента приобретения. В связи с этим особую важность в функционировании рынка основного капитала приобретает фактор времени.
В самом деле, деятельность любого производителя сопряжена с необходимостью осуществления капиталовложений, или инвестиций - расходования денежных средств в данный момент в расчете получить определенный доход в будущем. Чтобы принять разумное решение о покупке оборудования или строительстве новой очереди завода, фирме нужно сравнить предстоящие затраты с отдачей, которая будет получена благодаря им.
Принципиальное значение здесь имеет то, что затраты и доходы, связанные с инвестициями, имеют разную временную локализацию. Расходы следует сделать уже в настоящее время, а доходы они принесут лишь в будущем. Следовательно, для принятия обоснованного инвестиционного решения следует уметь сопоставлять текущую стоимость (сегодняшние затраты) с будущей стоимостью (потенциальные доходы). Каким же образом решается проблема измерения "современной стоимости будущих доходов"?
С экономической точки зрения одинаковые суммы, имеющие разную временную локализацию, отличаются по размерам. Действительно существование в экономике прибыльных вариантов инвестирования денежных средств дает возможность получать доход от любой имеющейся в настоящий момент суммы. Доходы же будущих периодов вплоть до своего реального поступления дополнительную прибыль приносить не могут.
Например, 100 руб., которыми человек располагая на 1 января 2003 г., могли быть положены в банк, обменены на доллары, вложены в акции российских предприятий и т.п. Если вложение денег оправдает себя, то к началу 2004 г. 100 руб. превратятся, скажем, в 150 руб. В то же время точно такая же сумма в 100 руб., получение которой, однако, предстоит только 1 января 2004 г., за весь 2003 г. не увеличится ни на копейку. Другими словами, если мы дождемся совпадения временных параметров (будем проводить сравнение обеих сумм 1 января 2004 г.), то убедимся, что современная денежная купюра оказалась в полтора раза ценнее такой же, но полученной позже (150 руб. против 100 руб.).
Сущность дисконтирования
Сопоставлять денежные суммы, получаемые в разное время, позволяет разработанный экономистами метод дисконтирования. Подобно мосту, соединяющему два противоположных берега, дисконтирование делает возможным сравнение денежных потоков, получаемых в разное время, путем приведения (пересчета) их к одному временному периоду.
Итак, мы установили, что одна и та же сумма денежных средств будет иметь большую ценность в данный момент времени по сравнению с будущим. Следовательно, для обеспечения сопоставимости текущих и будущих доходов нужно скорректировать будущие поступления в сторону уменьшения. Процедура дисконтирования как раз и состоит в уменьшении будущего дохода. Чтобы научиться определять количественные масштабы этого уменьшения, необходимо рассмотреть механизм образования будущего дохода.
Предположим, что в нашем распоряжении имеется 100 000 руб. При этом есть возможность вложения данной суммы на банковский счет, ставка по которому составляет 10% годовых. Тогда будущая стоимость инвестируемых нами сегодня 100 000 руб. через год составит 110 000 руб.:
Спустя 2 года текущая сумма возрастет до 121 000 руб.:

Через 3 года наш доход составит 133 100 руб.:
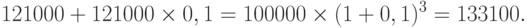
Легко понять, что в общем виде формула расчета будущего дохода будет:
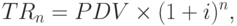 |
( 12.1) |
| где | TRn - совокупный доход n-го года; |
| PDV - текущая стоимость; | |
| n - число лет; | |
| i - процентная ставка. |
Текущая дисконтированная стоимость
Формула (12.1) позволяет рассчитать будущий совокупный доход сегодняшних капиталовложений. Используя ее, мы также можем решить обратную задачу: определить текущую стоимость будущего дохода
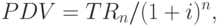
или
 |
( 12.2) |
где  - коэффициент дисконтирования.
- коэффициент дисконтирования.
Величину PDV, полученную путем умножения совокупного будущего дохода на коэффициент дисконтирования, еще называют текущей дисконтированной стоимостью будущего дохода, поскольку коэффициент дисконтирования позволяет уравнять будущую и текущую стоимости. А так как численное значение коэффициента дисконтирования всегда меньше единицы, то уравнивание происходит за счет уменьшения будущего совокупного дохода на величину, обратно пропорциональную ставке процента.
PDV инвестиционного фонда
До сих пор мы анализировали довольно редкую ситуацию, при которой капитал инвестируется на длительный срок, а все доходы получаются единовременно по его окончании. В реальных инвестиционных проектах чаще реализуется иная схема: доходы порциями поступают в течение всего срока осуществления проекта.
Пусть, например, некая фирма приобретает мощный компьютер (сервер) стоимостью 1 млн руб. Согласно бизнес-плану, сменить его более новой машиной предполагается через 3 года, а за это время в результате его внедрения будут получены следующие суммы валового (т.е. включающего амортизацию) дохода: в 1-й год - 400 тыс., во 2-й - 800в 3-й - 200 тыс. руб. В этом случае текущая дисконтированная стоимость всего проекта будет складываться из суммы дисконтированных стоимостей доходов каждого года:

Если принять, как и в прошлом примере, ставку процента за 10%, то в численной форме текущая дисконтированная стоимость составит:

В общем же виде формула текущей дисконтированной стоимости проекта, длящегося n лет, выглядит:
 |
( 12.3) |
PDV фиксированного дохода в бесконечном периоде
Еще один важный случай - оценка 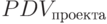 , когда доход постоянен по величине и выплачивается неограниченное число лет. В чистом виде такая ситуация типична для некоторых видов ценных бумаг - так называемых бессрочных облигаций и привилегированных акций (см.
"Предприятие как главный субъект микроэкономики"
). При их выпуске прямо оговаривается, что вложив некоторую сумму в определенную фирму, вы приобретаете право на стабильный доход на все время, пока существует эта компания.
, когда доход постоянен по величине и выплачивается неограниченное число лет. В чистом виде такая ситуация типична для некоторых видов ценных бумаг - так называемых бессрочных облигаций и привилегированных акций (см.
"Предприятие как главный субъект микроэкономики"
). При их выпуске прямо оговаривается, что вложив некоторую сумму в определенную фирму, вы приобретаете право на стабильный доход на все время, пока существует эта компания.
Присмотримся внимательно к формуле (12.3). Даже если число n будет стремиться к бесконечности, 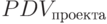 составит конечную величину. Дело в том, что чем дальше в будущее отдален некоторый фиксированный доход, тем меньшую величину он составляет. Ведь:
составит конечную величину. Дело в том, что чем дальше в будущее отдален некоторый фиксированный доход, тем меньшую величину он составляет. Ведь:
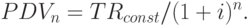
Числитель этой дроби по условиям выпуска названных ценных бумаг постоянен, а знаменатель с каждым годом возрастает, причем очень быстро (по экспоненте). Поэтому реальный вклад в величину 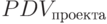 могут внести только несколько первых членов суммы, входящей в формулу (12.3). Все же последующие пренебрежительно малы и почти ничего к ней не добавляют. Математики называют ряды такого вида бесконечно убывающей геометрической прогрессией и давно вывели формулу для определения ее величины:
могут внести только несколько первых членов суммы, входящей в формулу (12.3). Все же последующие пренебрежительно малы и почти ничего к ней не добавляют. Математики называют ряды такого вида бесконечно убывающей геометрической прогрессией и давно вывели формулу для определения ее величины:
 |
( 12.4) |
Именно так может быть подсчитана цена привилегированной акции или бессрочной облигации, ибо все будущие доходы от нее в дисконтированной (приведенной к настоящему времени) форме составят ровно эту величину. Но, честно говоря, если бы формула (12.4) касалась только стоимости некоторых разновидностей ценных бумаг, ей вряд ли стоило бы уделять здесь место - слишком уж частный это вопрос.
Гораздо важнее то, что тому же закону в основном подчиняются все относительно постоянные доходы. Например, более или менее постоянную величину составляет рента с земельного участка, арендная плата за помещение, средний уровень дивидендов по акциям и т.д. Если доход от всех этих видов имущества будет колебаться от года к году на несколько или даже на десятки процентов, формула (12.4) все равно останется применимой. В самом деле, велика ли разница, если вы делите на бесконечность, на миллион, на десять тысяч или на любое другое очень большое число доход в 100 и 150 руб.? И в том, и в другом случаях получаются доли копейки.
Поэтому на практике формула (12.4) применима ко всем случаям неограниченно долго получаемых доходов, если они колеблются не слишком сильно. В дальнейшем мы убедимся, что по этой причине с ее помощью рассчитываются очень многие важные экономические параметры: цена земли, цена акции и т.п.
Критерий экономической обоснованности инвестиционного проекта
С помощью текущей дисконтированной стоимости мы научились приводить в соизмеримый вид произведенные затраты и получаемые в разное время доходы. Это дает возможность правильно оценить эффективность осуществляемых вложений и сделать выбор в пользу наиболее выгодного инвестиционного проекта. Показателем, позволяющим достоверно определить выгодность инвестиционного проекта, является чистая дисконтированная стоимость (NPV).
Будущий совокупный доход, приведенный к текущему периоду с помощью дисконтирования, есть текущая дисконтированная стоимость (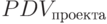 ). Размер понесенных фирмой затрат отражает осуществляемые ею инвестиции (I). Очевидно, что выгода от осуществления проекта (как раз ее-то и называют чистой дисконтированной стоимостью) будет измеряться разностью обеих величин и ее можно рассчитать по формуле
). Размер понесенных фирмой затрат отражает осуществляемые ею инвестиции (I). Очевидно, что выгода от осуществления проекта (как раз ее-то и называют чистой дисконтированной стоимостью) будет измеряться разностью обеих величин и ее можно рассчитать по формуле
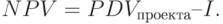 |
( 12.5) |
Из формулы (12.5) видно, что инвестирование будет выгодным в случае превышения получаемых доходов над произведенными вложениями, т.е. при положительном значении показателя чистой дисконтированной стоимости. Следовательно, если NPV > 0, инвестиционный проект можно считать вполне приемлемым, а вложение капитала целесообразным. В противном случае (NPV < 0) будет правильнее отказаться от намечаемого проекта, так как предполагаемые вложения не окупятся и фирма-инвестор понесет убытки.
Расчет чистой дисконтированной стоимости во многом упрощает решение стоящей перед любой фирмой сложной и одновременно жизненно важной задачи выбора наиболее выгодного инвестиционного проекта. Приведем условный пример такого расчета.
Допустим, намечаемый проект требует от предприятия вложения инвестиций в размере 20 тыс. руб. в машину, которая будет полностью амортизирована в течение четырех лет. Совокупный доход (включая амортизационные взносы), ожидаемый от данного проекта, достигнет суммы 5 тыс. руб. в 1-й и 2-й и 8 тыс. руб. в 3-й и 4-й годы. Необходимо определить выгодность проекта, учитывая, что ставка процента, составляет 10% в год. Иными словами, требуется определить чистую дисконтированную стоимость, т.е. сопоставить общие будущие поступления, приведенные к текущему периоду, и требуемые инвестиции. Решение задачи выглядит так:

Поскольку чистая дисконтированная стоимость в нашем примере имеет положительный знак, планируемый проект является благоприятным для фирмы. Он позволяет получить более высокий доход, чем при вложении денег в банк.
Обратим, однако, внимание и на то, насколько важное значение для принятия правильного решения имеет использование метода дисконтирования. Если бы мы действовали неправильно и просто сложили бы доходы за разные годы, как это обычно делают непрофессионалы, то проект показался бы нам очень выгодным (5000 + 5000 + 8000 + 8000 = 26000). Могло создаться впечатление, что, соглашаясь на его реализацию, мы выигрываем целых 6000 руб. В действительности выигрыш составляет лишь полторы сотни, т.е. проект находится буквально на грани приемлемости.

