Логика. Логические функции. Решение уравнений
Логические уравнения и системы уравнений
Пусть 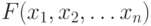 – логическая функция от n переменных. Логическое уравнение имеет вид:
– логическая функция от n переменных. Логическое уравнение имеет вид:
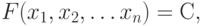
Константа С имеет значение 1 или 0.
Логическое уравнение может иметь от 0 до  различных решений. Если С равно 1, то решениями являются все те наборы переменных из таблицы истинности, на которых функция F принимает значение истина (1). Оставшиеся наборы являются решениями уравнения при C, равном нулю. Можно всегда рассматривать только уравнения вида:
различных решений. Если С равно 1, то решениями являются все те наборы переменных из таблицы истинности, на которых функция F принимает значение истина (1). Оставшиеся наборы являются решениями уравнения при C, равном нулю. Можно всегда рассматривать только уравнения вида:
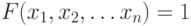
Действительно, пусть задано уравнение:
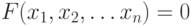
В этом случае можно перейти к эквивалентному уравнению:
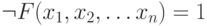
Рассмотрим систему из k логических уравнений:
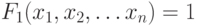
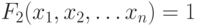
...
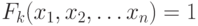
Решением системы является набор переменных, на котором выполняются все уравнения системы. В терминах логических функций для получения решения системы логических уравнений следует найти набор, на котором истинна логическая функция Ф, представляющая конъюнкцию исходных функций  :
:
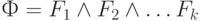
Если число переменных невелико, например, менее 5, то нетрудно построить таблицу истинности для функции  , что позволяет сказать, сколько решений имеет система и каковы наборы, дающие решения.
, что позволяет сказать, сколько решений имеет система и каковы наборы, дающие решения.
В некоторых задачах ЕГЭ по нахождению решений системы логических уравнений число переменных доходит до значения 10. Тогда построить таблицу истинности становится практически неразрешимой задачей. Для решения задачи требуется другой подход. Для произвольной системы уравнений не существует общего способа, отличного от перебора, позволяющего решать такие задачи.
В предлагаемых на экзамене задачах решение обычно основано на учете специфики системы уравнений. Повторяю, кроме перебора всех вариантов набора переменных, общего способа решения задачи нет. Решение нужно строить исходя из специфики системы. Часто полезно провести предварительное упрощение системы уравнений, используя известные законы логики. Другой полезный прием решения этой задачи состоит в следующем. Нам интересны не все наборы, а только те, на которых функция  имеет значение 1. Вместо построения полной таблицы истинности будем строить ее аналог - бинарное дерево решений. Каждая ветвь этого дерева соответствует одному решению и задает набор, на котором функция
имеет значение 1. Вместо построения полной таблицы истинности будем строить ее аналог - бинарное дерево решений. Каждая ветвь этого дерева соответствует одному решению и задает набор, на котором функция  имеет значение 1. Число ветвей в дереве решений совпадает с числом решений системы уравнений.
имеет значение 1. Число ветвей в дереве решений совпадает с числом решений системы уравнений.
Что такое бинарное дерево решений и как оно строится, поясню на примерах нескольких задач.
Задача 18
Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, которые удовлетворяют системе из двух уравнений?
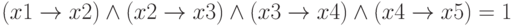
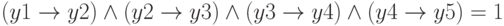
Ответ: Система имеет 36 различных решений.
Решение: Система уравнений включает два уравнения. Найдем число решений для первого уравнения, зависящего от 5 переменных – 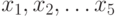 . Первое уравнение можно в свою очередь рассматривать как систему из 5 уравнений. Как было показано, система уравнений фактически представляет конъюнкцию логических функций. Справедливо и обратное утверждение, - конъюнкцию условий можно рассматривать как систему уравнений.
. Первое уравнение можно в свою очередь рассматривать как систему из 5 уравнений. Как было показано, система уравнений фактически представляет конъюнкцию логических функций. Справедливо и обратное утверждение, - конъюнкцию условий можно рассматривать как систему уравнений.
Построим дерево решений для импликации ( ) - первого члена конъюнкции, который можно рассматривать как первое уравнение. Вот как выглядит графическое изображение этого дерева
) - первого члена конъюнкции, который можно рассматривать как первое уравнение. Вот как выглядит графическое изображение этого дерева
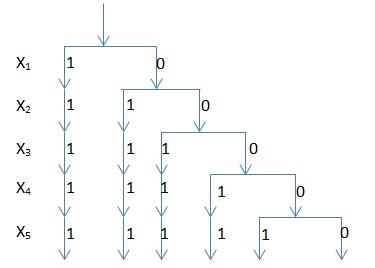
Дерево состоит из двух уровней по числу переменных уравнения. Первый уровень описывает первую переменную 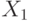 . Две ветви этого уровня отражают возможные значения этой переменной – 1 и 0. На втором уровне ветви дерева отражают только те возможные значения переменной
. Две ветви этого уровня отражают возможные значения этой переменной – 1 и 0. На втором уровне ветви дерева отражают только те возможные значения переменной  , для которых уравнение принимает значение истина. Поскольку уравнение задает импликацию, то ветвь, на которой
, для которых уравнение принимает значение истина. Поскольку уравнение задает импликацию, то ветвь, на которой 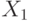 имеет значение 1, требует, чтобы на этой ветви
имеет значение 1, требует, чтобы на этой ветви  имело значение 1. Ветвь, на которой
имело значение 1. Ветвь, на которой 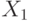 имеет значение 0, порождает две ветви со значениями
имеет значение 0, порождает две ветви со значениями  , равными 0 и 1. Построенное дерево задает три решения, на которых импликация
, равными 0 и 1. Построенное дерево задает три решения, на которых импликация  принимает значение 1. На каждой ветви выписан соответствующий набор значений переменных, дающий решение уравнения.
принимает значение 1. На каждой ветви выписан соответствующий набор значений переменных, дающий решение уравнения.
Вот эти наборы: {(1, 1), (0, 1), (0, 0)}
Продолжим построение дерева решений, добавляя следующее уравнение, следующую импликацию  . Специфика нашей системы уравнений в том, что каждое новое уравнение системы использует одну переменную из предыдущего уравнения, добавляя одну новую переменную. Поскольку переменная
. Специфика нашей системы уравнений в том, что каждое новое уравнение системы использует одну переменную из предыдущего уравнения, добавляя одну новую переменную. Поскольку переменная  уже имеет значения на дереве, то на всех ветвях, где переменная
уже имеет значения на дереве, то на всех ветвях, где переменная  имеет значение 1, переменная
имеет значение 1, переменная  также будет иметь значение 1. Для таких ветвей построение дерева продолжается на следующий уровень, но новые ветви не появляются. Единственная ветвь, где переменная
также будет иметь значение 1. Для таких ветвей построение дерева продолжается на следующий уровень, но новые ветви не появляются. Единственная ветвь, где переменная  имеет значение 0, даст разветвление на две ветви, где переменная
имеет значение 0, даст разветвление на две ветви, где переменная  получит значения 0 и 1. Таким образом, каждое добавление нового уравнения, учитывая его специфику, добавляет одно решение. Исходное первое уравнение:
получит значения 0 и 1. Таким образом, каждое добавление нового уравнения, учитывая его специфику, добавляет одно решение. Исходное первое уравнение:
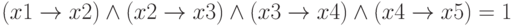
имеет 6 решений. Вот как выглядит полное дерево решений для этого уравнения:
Второе уравнение нашей системы аналогично первому:
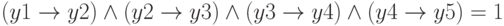
Разница лишь в том, что в уравнении используются переменные Y. Это уравнение также имеет 6 решений. Поскольку каждое решение для переменных 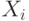 может быть скомбинировано с каждым решением для переменных
может быть скомбинировано с каждым решением для переменных 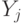 , то общее число решений равно 36.
, то общее число решений равно 36.
Заметьте, построенное дерево решений дает не только число решений (по числу ветвей), но и сами решения, выписанные на каждой ветви дерева.
Задача 19
Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, которые удовлетворяют всем перечисленным ниже условиям?
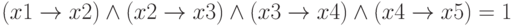
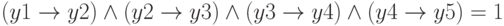
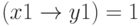
Ответ: 31
Решение:
Эта задача является модификацией предыдущей задачи. Разница в том, что добавляется еще одно уравнение, связывающее переменные X и Y.
Из уравнения  следует, что когда
следует, что когда 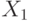 имеет значение 1(одно такое решение существует), то и
имеет значение 1(одно такое решение существует), то и  имеет значение 1. Таким образом, существует один набор, на котором
имеет значение 1. Таким образом, существует один набор, на котором 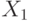 и
и  имеют значения 1. При
имеют значения 1. При 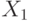 , равном 0,
, равном 0,  может иметь любое значение, как 0, так и 1. Поэтому каждому набору с
может иметь любое значение, как 0, так и 1. Поэтому каждому набору с 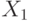 , равном 0, а таких наборов 5, соответствует все 6 наборов с переменными Y. Следовательно, общее число решений равно 31.
, равном 0, а таких наборов 5, соответствует все 6 наборов с переменными Y. Следовательно, общее число решений равно 31.
Задача 20
Сколько решений имеет уравнение:
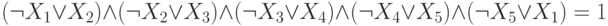
Ответ: 2
Решение: Вспоминания основные эквивалентности, запишем наше уравнение в виде:
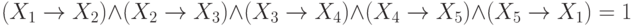
Циклическая цепочка импликаций означает тождественность переменных, так что наше уравнение эквивалентно уравнению:
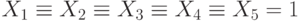
Это уравнение имеет два решения, когда все 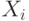 равны либо 1, либо 0.
равны либо 1, либо 0.
Задача 21
Сколько решений имеет уравнение:
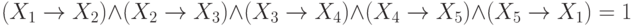
Ответ: 4
Решение: Так же, как и в задаче 20, от циклических импликаций перейдем к тождествам, переписав уравнение в виде:
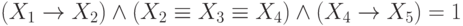
Построим дерево решений для этого уравнения:
Задача 22
Сколько решений имеет следующая система уравнений?
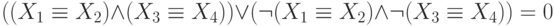
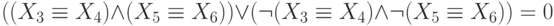
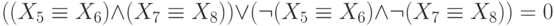
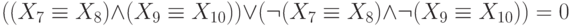
Ответ: 64
Решение: Перейдем от 10 переменных к 5 переменным, введя следующую замену переменных:
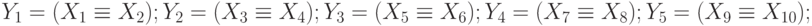
Тогда первое уравнение примет вид:
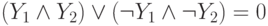
Уравнение можно упростить, записав его в виде:
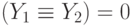
Переходя к традиционной форме, запишем систему после упрощений в виде:




Дерево решений для этой системы простое и состоит из двух ветвей с чередующимися значениями переменных:
Возвращаясь к исходным переменным  , заметим, что каждому значению переменной
, заметим, что каждому значению переменной  соответствует 2 значения переменных
соответствует 2 значения переменных  , поэтому каждое решение в переменных
, поэтому каждое решение в переменных  порождает
порождает 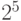 решений в переменных
решений в переменных  . Две ветви порождают
. Две ветви порождают  решений, так что общее число решений равно 64.
решений, так что общее число решений равно 64.
Как видите, каждая задача на решение системы уравнений требует своего подхода. Общим приемом является выполнение эквивалентных преобразований для упрощения уравнений. Общим приемом является и построение деревьев решений. Применяемый подход частично напоминает построение таблицы истинности с той особенностью, что строятся не все наборы возможных значений переменных, а лишь те, на которых функция принимает значение 1 (истина). Часто в предлагаемых задачах нет необходимости в построении полного дерева решений, поскольку уже на начальном этапе удается установить закономерность появления новых ветвей на каждом следующем уровне, как это сделано, например, в задаче 18.
В целом задачи на нахождение решений системы логических уравнений являются хорошими математическими упражнениями.
Если задачу трудно решить вручную, то можно поручить решение задачи компьютеру, написав соответствующую программу решения уравнений и систем уравнений.
Написать такую программу несложно. Такая программа легко справится со всеми задачами, предлагаемыми в ЕГЭ.
Как это ни странно, но задача нахождения решений систем логических уравнений является сложной и для компьютера, оказывается и у компьютера есть свои пределы. Компьютер может достаточно просто справиться с задачами, где число переменных 20 -30, но начнет надолго задумываться на задачах большего размера. Дело в том, что функция  , задающая число наборов, является экспонентой, быстро растущей с увеличением n. Настолько быстро, что обычный персональный компьютер за сутки не справится с задачей, у которой 40 переменных.
, задающая число наборов, является экспонентой, быстро растущей с увеличением n. Настолько быстро, что обычный персональный компьютер за сутки не справится с задачей, у которой 40 переменных.