Основные графические примитивы OpenGL и их свойства

Упражнения. Построение графиков функций

Пример выполнения задания

Задание: Постройте график функции . Реализуйте возможность интерактивного изменения коэффициентов и с помощью клавиатуры.

Выполнение задания

Для построения графиков функций часто удобно использовать примитив "ломаная линия", в котором каждый следующий отрезок строится как продолжение предыдущего отрезка. В качестве основы для программы можно использовать приложение, созданное в "Структура приложений, использующих OpenGL" .

Построение графика можно выполнить в обработчике события OnPaint формы на Object Pascal и события Paint компонента GLControl на C#. Код для построения графика функции можно расположить непосредственно после фрагмента кода, выполняющего построение осей координат. Для реализации также необходимо будет использовать глобальные переменные:

C#:
double n = 1;
double z = 1;

Object Pascal:
var
  n: double =1;
  z: double =1;

График функции может быть построен с помощью фрагмента, приведенного ниже:

C#:
GL.Color3(1f, 0, 0);
GL.Begin(BeginMode.LineStrip);
for (int i = -50; i <= 50; ++i)
{
double x = i * 0.1;
GL.Vertex2(x, Math.Sin(x*n)*z);
}
GL.End();
Object Pascal:
glColor3f(1, 0, 0);
glBegin (GL_LINE_STRIP);
  for i:=-50 to 50 do
  begin
    x := i*0.1;
    glVertex2f (x, Sin(x*n)*z);
  end;
glEnd;

В этом фрагменте кода предполагается, что область видимости вдоль направления оси OX будет не менее 10 единиц. Изменить размер сцены можно в обработчике события изменения размеров формы в программе на Object Pascal и изменения размеров графического компонента GLControl на C#.

C#:
private void glControl1_Resize(object sender, EventArgs e)
{
GL.Viewport(0, 0, glControl1.Width, glControl1.Height);
GL.MatrixMode(MatrixMode.Projection);
GL.LoadIdentity();
GL.Ortho(-6, 6, -6, 6, -6, 6);
GL.MatrixMode(MatrixMode.Modelview);
glControl1.Invalidate();
}

Object Pascal:
procedure TfrmMain.FormResize(Sender: TObject);
begin
 glViewport(0, 0, ClientWidth, ClientHeight);
 glMatrixMode(GL_PROJECTION);
 glLoadIdentity;
 glOrtho(-6, 6, -6, 6, -6, 6);
 glMatrixMode(GL_MODELVIEW);
 InvalidateRect(Handle, nil, False);
end;

Для уменьшения и увеличения значения переменной n можно использовать клавиши со стрелками влево и вправо. Уменьшение и увеличение значения параметра z можно реализовать с помощью клавиш со стрелками вниз и вверх.

C#:
private void glControl1_PreviewKeyDown(object sender, PreviewKeyDownEventArgs e)
{
  switch (e.KeyCode)
  {
    case Keys.Insert: AngleX += AngleDl; break;
    case Keys.Delete: AngleX -= AngleDl; break;
case Keys.Home: AngleY += AngleDl; break;
case Keys.End: AngleY -= AngleDl; break;
case Keys.Prior: AngleZ += AngleDl; break;
case Keys.Next: AngleZ -= AngleDl; break;
case Keys.Up: z += 0.1; break;
case Keys.Down: z -= 0.1; break;
case Keys.Left: n -= 0.1; break;
case Keys.Right: n += 0.1; break;
}
glControl1.Invalidate();
Text =
  String.Format("График функции y = {0}*Sin(x*{1})", z, n);
}
Object Pascal:
procedure TfrmMain.FormKeyDown(Sender: TObject; var Key: Word;
  Shift: TShiftState);
begin
 If Key = VK_ESCAPE then Close;
 case Key of
  VK_INSERT: inc(AngleX, AngleDl);
  VK_DELETE: dec(AngleX, AngleDl);
  VK_HOME:   inc(AngleY, AngleDl);
  VK_END:    dec(AngleY, AngleDl);
  VK_PRIOR:  inc(AngleZ, AngleDl);
  VK_NEXT:   dec(AngleZ, AngleDl);
  VK_UP:     z := z + 0.1;
  VK_DOWN:   z := z - 0.1;
  VK_LEFT:   n := n - 0.1;
  VK_RIGHT:  n := n + 0.1;
 end;
 InvalidateRect(Handle, nil, False);
Caption := 'График функции y = '+ FloatToStr(z) +'    *Sin(x*'+FloatToStr(n)+')';
end;

Задания

1. Постройте график функции 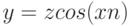. Реализуйте возможность интерактивного изменения коэффициентов и с помощью клавиатуры.
2. Постройте график функции кохлеоиды, уравнение которой в полярной системе координат: 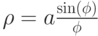. Реализуйте возможность интерактивного изменения коэффициента с помощью клавиатуры.
3. Постройте график функции лемниската Бернулли, уравнение которой в полярной системе координат: 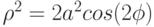. Реализуйте возможность интерактивного изменения коэффициента с помощью клавиатуры.
4. Постройте график функции синусоидальной спирали, уравнение которой в полярной системе координат , при и 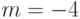. Реализуйте возможность интерактивного изменения коэффициента с помощью клавиатуры.
5. Постройте график функции овала Кассини, уравнение которой в полярных координатах . Реализуйте возможность интерактивного изменения коэффициентов и с помощью клавиатуры.
6. Постройте график функции розы, уравнение которой в полярных координатах . Реализуйте возможность интерактивного изменения коэффициента с помощью клавиатуры.
7. Постройте график спирали Ферма, уравнение которой в полярных координатах 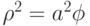. Реализуйте возможность интерактивного изменения коэффициента с помощью клавиатуры.
8. Постройте график функции, уравнение которой .
9. Постройте график функции эллипса 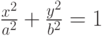. Реализуйте возможность интерактивного изменения коэффициентов и с помощью клавиатуры.