Методы классификации и прогнозирования. Метод опорных векторов. Метод "ближайшего соседа". Байесовская классификация
В предыдущих лекциях мы рассмотрели такие методы классификации и прогнозирования как линейная регрессия и деревья решений; в этой лекции мы продолжим знакомство с методами этой группы и рассмотрим следующие из них: метод опорных векторов, метод ближайшего соседа (метод рассуждений на основе прецедентов ) и байесовскую классификацию.
Метод опорных векторов
Метод опорных векторов (Support Vector Machine - SVM) относится к группе граничных методов. Она определяет классы при помощи границ областей.
При помощи данного метода решаются задачи бинарной классификации.
В основе метода лежит понятие плоскостей решений.
Плоскость (plane) решения разделяет объекты с разной классовой принадлежностью.
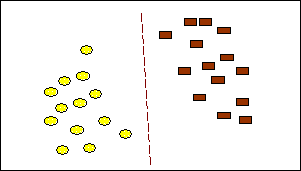
На рис.10.1 приведен пример, в котором участвуют объекты двух типов. Разделяющая линия задает границу, справа от которой - все объекты типа brown (коричневый), а слева - типа yellow (желтый). Новый объект, попадающий направо, классифицируется как объект класса brown или - как объект класса yellow, если он расположился по левую сторону от разделяющей прямой. В этом случае каждый объект характеризуется двумя измерениями.
Цель метода опорных векторов - найти плоскость, разделяющую два множества объектов; такая плоскость показана на рис. 10.2. На этом рисунке множество образцов поделено на два класса: желтые объекты принадлежат классу А, коричневые - классу В.
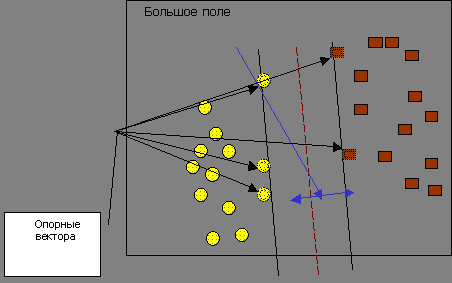
Метод отыскивает образцы, находящиеся на границах между двумя классами, т.е. опорные вектора ; они изображены на рис. 10.3.
Опорными векторами называются объекты множества, лежащие на границах областей.
Классификация считается хорошей, если область между границами пуста.
На рис. 10.3.показано пять векторов, которые являются опорными для данного множества.