НОУ ИНТУИТ | Табличный процессор Excel в экономических и финансовых расчетах. Лекция 16: Решение задач по прогнозированию рынка

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.05.2021 | Доступ: платный | Студентов: 8 / 3 | Длительность: 14:25:00

Темы: Офисные технологии, Программное обеспечение, Экономика

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Цель работы: Научиться выполнять статистический анализ и прогнозирование стационарных показателей в табличном процессоре Excel. Содержание работы: Предварительная обработка исходной информации для прогнозирования. Прогнозирование стационарных показателей. Порядок выполнения работы: Изучить методические указания. Выполнить задания. Оформить отчет и ответить на контрольные вопросы.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Предварительная обработка исходной информации для прогнозирования

Задания

1. Анализируются объемы ежедневных продаж некоторого товара за 60 дней. Получены следующие данные (в штуках): 5, 6, 3, 2, 7, 7, 6, 6, 10, 11, 6, 4, 5, 6, 3, 12, 9, 10, 7, 4, 6, 7, 8, 8, 10, 5, 5, 4, 3, 6, 6, 7, 7, 8, 8, 10, 6, 4, 5, 6, 12, 7, 7, 8, 11, 9, 10, 5, 6, 4, 2, 7, 11, 8, 7, 9, 5, 6, 9, 5.

Необходимо:

а) построить статистический ряд;

б) с помощью встроенных функций Excel (Формулы > Другие функции > Статистические) определить выборочные характеристики:

минимальное значение (функция МИН);
максимальное значение (МАКС);
размах выборки;
среднюю величину (СРЗНАЧ);
моду (МОДА);
медиану (МЕДИАНА);
среднее линейное отклонение (СРОТКЛ);
дисперсию (ДИСП);
среднеквадратическое отклонение (СТАНДОТКЛОН);
показатели вариации размаха, линейного и квадратического отклонения;
асимметрию (СКОС);
эксцесса (ЭКСЦЕСС);

в) получить вышеперечисленные характеристики с помощью инструмента Описательная статистика (Данные> Анализ данных); (если этого инструмента нет, то установите его: > Параметры Excel > Надстройки > Пакет Анализа > Перейти > ОК)

г) построить таблицу эмпирического распределения частот (воспользовавшись функцией Формулы > Другие функции > Статистические > СЧЁТЕСЛИ) и его график, оценить характер распределения визуально и посредством показателей асимметрии и эксцесса;

д) построить по эмпирическим данным нормальное распределение частот (Формулы > Другие функции > Статистические > НОРМРАСП), оценить соответствие ему фактических данных по критерию Пирсона 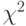$\chi^{2}$ (Формулы > Другие функции > Статистические > ХИ2ТЕСТ).

Результаты выполнения пунктов г) и д) оформить в виде таблицы 16.1.

Таблица 16.1. Фактическое и нормальное распределение частот
Значение объема продаж X	…	Итого
Фактическая частота:
абсолютная f
относительная 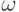$\omega$
Теоретическая (нормальная) частота:
абсолютная f_т
относительная 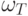$\omega_{T}$
Примечание: количество промежуточных столбцов соответствует числу встречающихся различных значений объёмов продаж

Для е построить полигон относительных частот фактического и нормального распределения.

2. Анализируется продолжительность телефонных разговоров с клиентами некоторой справочной службы. Случайным образом отобраны 60 телефонных разговоров и зафиксированы их длительности (в секундах): 39, 60, 40, 52, 32, 68, 77, 61, 68, 60, 47, 49, 70, 55, 66, 80, 35, 67, 70, 55, 42, 52, 60, 82, 70, 55, 47, 39, 50, 58, 45, 50, 53, 33, 49, 54, 55, 70, 62, 60, 60, 40, 59, 64, 70, 55, 54, 35, 48, 52, 57, 55, 82, 70, 51, 35, 49, 60, 55, 47.

Необходимо:

а) вычислить выборочное среднее значение, дисперсию, среднеквадратическое отклонение;

б) построить интервальный статистический ряд, включающий 5 интервалов и вычислить на его основании выборочные характеристики; построить гистограмму распределения частот.

Для выполнения задания использовать таблицу 16.2.

Таблица 16.2. Интервальный ряд
Границы интервала [от; до)	...	Итого
Частота f
Середина интервала X_ср.инт		-
Квадрат отклонения середины интервала от среднего значения интервального ряда (Х_ср.инт – Х_ср)²
Примечание: количество промежуточных столбцов соответствует числу интервалов

Длина интервала определяется путем деления размаха выборки на количество интервалов.

Среднее значение интервального ряда X_ср рассчитывается по формуле:

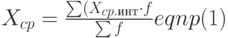
$X_{cp}=\frac{\sum(X_{cp.инт}\cdot f}{\sum f}eqnp(1)$

Дисперсия интервального ряда рассчитывается по формуле:

$\sigma^{2}=\frac{\sum((X_{cp.инт}-X_{cp})^{2}\cdot f)}{\sum f}\eqno(2)$

в) построить интервальный статистический ряд, включающий 8 интервалов и вычислить на его основании выборочные характеристики (аналогично предыдущему пункту); построить гистограмму распределения частот;

г) сравнить результаты вычислений в пунктах а), б), в).

3. В таблице 16.3 приведены данные за 10 лет по количеству вновь регистрируемых фирм Х и по количеству банкротств Y в некотором государстве.

Таблица 16.3. Исходные данные
Год	X	Y	Год	X	Y
1	72 500	1 020	6	82 500	3 000
2	72 900	1 290	7	87 000	4 000
3	74 150	1 830	8	86 500	4 200
4	73 500	2 250	9	90 000	4 500
5	78 350	2 500	10	89 000	4 000

Дайте ответы на вопросы:

а) каково ожидаемое количество вновь регистрируемых фирм в течение года для данного временного интервала; какова выборочная дисперсия и среднеквадратическое отклонение для этого показателя?

б) каково ожидаемое количество банкротств в течение года для данного временного интервала; какова выборочная дисперсия и среднеквадратическое отклонение для этого показателя?

в) постройте графики анализируемых величин. Являются ли они независимыми? Вычислите коэффициент корреляции между X и Y (Формулы > Другие функции > Статистические > КОРРЕЛ). Оцените значимость коэффициента корреляции с помощью t-критерия Стьюдента.

Расчетное значение критерия tрасч определяется по формуле:

$t_{расч}=\frac{r\sqrt{n-2}}{1-r^{2}}\eqno(3),$

где: r – коэффициент корреляции;

n – число наблюдений.

Табличное значение критерия tтабл определяется с помощью встроенной функции СТЬЮДРАСПОБР (Формулы > Другие функции > Статистические) при уровне значимости 0,05 и числе степеней свободы.

Коэффициент корреляции признается значимым, если t_расч >t_табл

Прогнозирование стационарных показателей

_{Задания}

1. В таблице 16.4 приведены данные об объемах продаж некоторого товара в течение года.

Таблица 16.4. Информация о продажах товара
Номер месяц (n)	1	2	3	4	5	6	7	8	9	10	11	12
Продажи, млн р. (y)	1025	1043	1067	1028	983	1034	1042	1028	1047	1061	1023	1046

Необходимо:

а) построить график и визуально определить, является ли ряд стационарным;

б) дать прогноз продаж на 13-й месяц:

по среднему уровню всего года, последнего полугодия, последнего квартала;
по последним четырем месяцам методом простой средней, а также взвешенной средней, учитывающей большую значимость последних измерений.

Сравните полученные результаты.

2. По данным таблицы 16.4:

а) сгладить временной ряд методом скользящей средней по трем и пяти точкам. При этом формулы сглаживания для крайних точек будут иметь вид:

при сглаживании по трем точкам:

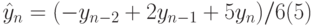
$\hat{y}_{1}=(5y_{1}+2y_{2}-y_{3})/6\eqno(4)$ $\hat{y}_{n}=(-y_{n-2}+2y_{n-1}+5y_{n})/6\eqno(5)$

где 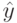$\hat{y}$ – сглаженный уровень ряда;

при сглаживании по пяти точкам:

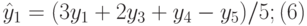
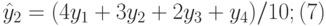
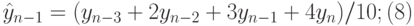
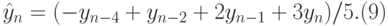
$\hat{y}_{1}=(3y_{1}+2y_{3}+y_{4}-y_{5})/5;\eqno(6)$ $\hat{y}_{2}=(4y_{1}+3y_{2}+2y_{3}+y_{4})/10;\eqno(7)$ $\hat{y}_{n-1}=(y_{n-3}+2y_{n-2}+3y_{n-1}+4y_{n})/10;\eqno(8)$ $\hat{y}_{n}=(-y_{n-4}+y_{n-2}+2y_{n-1}+3y_{n})/5.\eqno(9)$

Результаты отразить на графике и визуально определить, какое сглаживание наиболее соответствует экономическому процессу, заданному временным рядом;

б) сгладить временной ряд методом экспоненциального сглаживания, приняв параметр экспоненциального сглаживания равным 0,1 и 0,3:

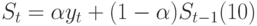
$S_{t}=\alpha y_{t}+(1-\alpha)S_{t-1}\eqno(10)$

где: S_t – сглаженный уровень t-го месяца. При этом в качестве S0 следует взять первый уровень ряда y₁;

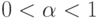$\alpha$ – параметр сглаживания ( $0<\alpha <1$ ).

Результаты отразить на графике и визуально определить, какой параметр сглаживания наиболее соответствует экономическому процессу, заданному временным рядом;

в) выполнить задания а) и б) с использованием инструментов анализа данных (Данные> Анализ данных) Скользящее среднее и Экспоненциальное сглаживание.

3. В таблице 16.5 приведены данные об объемах продаж некоторого товара в течение трех лет.

Таблица 16.5. Информация о продажах товара в миллионах рублей
Номер года (i)	Номер месяца (j)
Номер года (i)	1	2	3	4	5	6	7	8	9	10	11	12
1	940	900	1144	1173	1305	1309	1374	1374	1241	1269	1068	1045
2	915	802	1087	1201	1396	1439	1441	1445	1356	1339	1240	1205
3	884	1018	1164	1249	1328	1363	1388	1382	1311	1296	1201	1075

Необходимо:

а) построить на одном рисунке графики динамики продаж по годам и определить наличие сезонности;

б) рассчитать индексы сезонности по месяцам и построить сезонную волну:

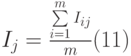
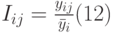
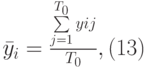
$I_{j}=\frac{\sum\limits_{i=1}^{m}I_{ij}}{m}\eqno(11)$ $I_{ij}=\frac{y_{ij}}{\bar{y}_{i}}\eqno(12)$ $\bar{y}_{i}=\frac{\sum\limits_{j=1}^{T_{0}}y{ij}}{T_{0}},\eqno(13)$

где: Т₀ – количество внутригодовых периодов (месяцев);

m – количество лет;

в) дать помесячный прогноз объемов продаж на 4-й год, если годовой объем прогнозируется на уровне 14 642 млн. руб.

Примечание. Выбор варианта:

При выполнении Задания 1 об объемах ежедневных продаж некоторого товара в течение 60 дней и Задания 3 о количестве вновь регистрируемых фирм и банкротств раздела "Предварительная обработка исходной информации для прогнозирования" к каждому члену заданной совокупности исходных величин прибавить номер вашего варианта в соответствии с номером в списке группы.
При выполнении Задания 2 раздела "Предварительная обработка исходной информации для прогнозирования", а также Заданий 1-3 раздела "Прогнозирование стационарных показателей" умножить все элементы заданной совокупности исходных величин на коэффициент 1,ху, где ху – цифры номера вашего варианта в соответствии с номером в списке группы. Например, если номер вашего варианта 1, то ху = 01 и исходные данные следует умножить на коэффициент 1,01. Если номер вашего варианта 13, то ху = 13 и исходные данные следует умножить на коэффициент 1,13.

КОНТРОЛЬНЫЕ ВОПРОСЫ

Дайте понятие статистического ряда. Что такое точечный и интервальный ряды?
Какие выборочные характеристики вы знаете? Как их рассчитать и что они характеризуют?
Что такое нормальное распределение случайной величины? Какова область его применения? Как оценить характер распределения эмпирических данных?
Что такое корреляция? Как можно оценить ее степень?
Что такое стационарный ряд? Как можно осуществлять прогнозирование таких показателей?
Дайте понятие сглаживания экономического ряда. Для чего оно осуществляется?
Охарактеризуйте метод скользящей средней.
Охарактеризуйте метод экспоненциального сглаживания.
Что такое сезонность и как она влияет на экономические процессы? Как можно количественно оценить сезонность?

Дальше >>

Авторизоваться

Табличный процессор Excel в экономических и финансовых расчетах

Решение задач по прогнозированию рынка

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Предварительная обработка исходной информации для прогнозирования

Прогнозирование стационарных показателей

КОНТРОЛЬНЫЕ ВОПРОСЫ

Вопросы и ответы