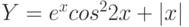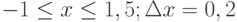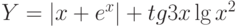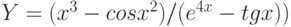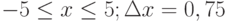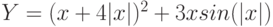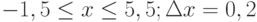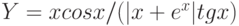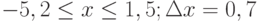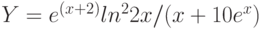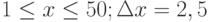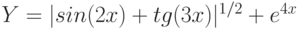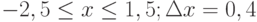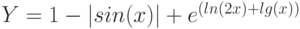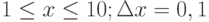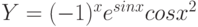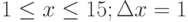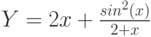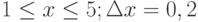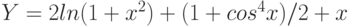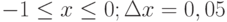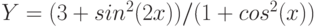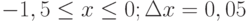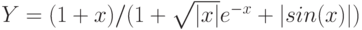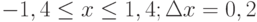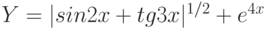Home

Lecture

НИУ ВШЭ (Высшая Школа Бизнес-Информатики):

Excel Spreadsheet in Economic and Financial Calculations
[+]
Опубликован: 26.05.2021 | Access: paid | Students: 8 / 3 | Длительность: 14:25:00
Themes: Офисные технологии, Программное обеспечение, Экономика
| | Share | | Download e-book
Lecture 3:

Встроенные функции. Статистический анализ. Работа с математическими и статистическими функциями
A
|
версия для печати
< Lecture 2 || Lecture 3 || Lecture 4 >
Annotation: Цель работы: научиться работать с Мастером функций, проводить анализ данных. Содержание работы: Использование Мастера функций. Анализ статистических данных. Инструменты пакета анализа. Порядок выполнения работы: Изучить методические указания. Выполнить задания. Оформить отчет и ответить на контрольные вопросы.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Математические функции

MS EXCEL обеспечивает 10 разных категорий функций: математические/тригонометрические, инженерные, логические, текстовые, статистические, функции категории дата/время, функции для работы с базами данных/списками, финансовые, информационные и функции категории ссылки/массивы.

Программа EXCEL содержит более 400 встроенных функций, которые можно выбрать с помощью Мастера функций.

Формулы, содержащие функции, можно вводить непосредственно в ячейку, в строку формул или создавать с помощью Мастера функций

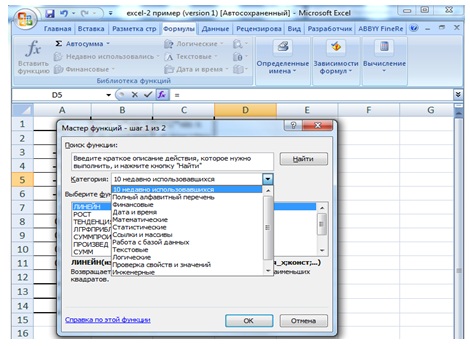
Для вызова Мастера функций необходимо выбрать команду Вставить функциюfx из меню Формулы или нажать на панели инструментов формула кнопку

После её нажатия появится окно Мастера функций (рис. 3.1 рис. 3.1).

Запуск Мастера функций

Рис. 3.1. Запуск Мастера функций

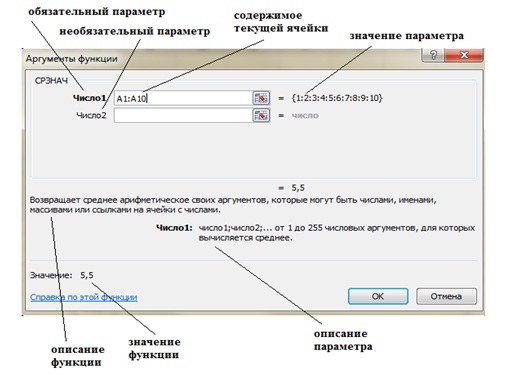
В открывшемся диалоговом окне выберите категорию и имя функции, а затем в полях с соответствующими подсказками введите аргументы (рис. 3.2 рис. 3.2). После нажатия кнопки ОК, готовая функция появится в строке формул

Вызов функции состоит в указании в формуле имени функции, после которого в скобках указывается список параметров (аргументов). Отдельные параметры (аргументы) разделяются в списке точкой с запятой.

Диалоговое окно Аргументы функции СРЗНАЧ (A1:A10)

Рис. 3.2. Диалоговое окно Аргументы функции СРЗНАЧ (A1:A10)

В качестве аргумента может использоваться число, адрес ячейки или произвольное выражение, для вычисления которого также могут использоваться функции.

Аргументы функций:

  1. числовые константы, например, функция ПРОИЗВЕД(2;3) вычисляет произведение чисел 2 и 3, т.е. 2•3.
  2. ссылки на ячейки и блоки ячеек (функция ПРОИЗВЕД (А1;С1:СЗ) вычисляет произведение содержимого ячеек А1,С1,С2 и С3, т.е. А1•С1•С2•СЗ.
  3. текстовые константы (заключенные в кавычки).
  4. логические значения.
  5. массивы.
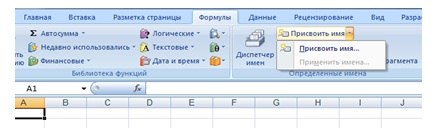
  6. имена ссылок, например, если ячейке А10 присвоить имя СУММА –последовательность команд Формулы \ Присвоить имя... – рис. 3.3 рис. 3.3), а блоку ячеек В10:Е10 – имя ИТОГИ, то допустима следующая запись: =СУММ(СУММА;ИТОГИ).
  7. смешанные аргументы, например, =СРЗНАЧ (Группа;АЗ;5*3)
Присвоение имени ячейке или блоку ячеек

Рис. 3.3. Присвоение имени ячейке или блоку ячеек

Пример 1. Вычислить значения функции

Y=ex*sin(x) для \[ $-1\geq x \leq 1$ \] \[ $\Delta x=0.1$ \]

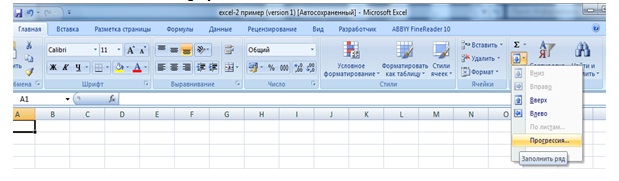
  1. Заполним столбец А значениями аргумента функции. Чтобы не вводить их вручную, применим следующий прием. Введите в ячейку А1 начальное значения аргумента (-1). Во вкладке Главная> Редактирование выберите кнопку Заполнить, затем Прогрессия и в открывшемся диалоговом окне укажите предельное значение (1), шаг(0,2) и направление По столбцам (рис. 3.4 рис. 3.4). После нажатия кнопки ОК в столбце А будут введены все значения аргумента
Автозаполнение ячеек

Рис. 3.4. Автозаполнение ячеек
  1. В ячейку В1 введите формулу =exp(А1)*sin(A1). Размножьте эту формулу на остальные ячейки столбца B, ухватив левой мышью маркер заполнения (черный квадратик в правом нижнем углу рамки выделенной ячейки B1) и протащив маркер до конца изменения аргумента. В итоге будут вычислены соответствующие значения функции.

Логические функции

Принцип действия большинства логических функций EXCEL заключается в проверке некоторого условия и выполнения в зависимости от него тех или иных действий.

Так, функция ЕСЛИ выполняет проверку условия, задаваемого первым аргументом логич_выр:

=ЕСЛИ(логич_выр; знач_да; знач_нет) и возвращает знач_да, если условие выполнено (ИСТИНА), и знач_нет, в противном случае (ЛОЖЬ).

Например:

  =ЕСЛИ(А6<10;5;10).

Если значение в ячейке А6<10, то функция вернет результат 5, а иначе – 10.

  =ЕСЛИ(B4>80;"Сданы";"Не сданы").

Если значение в ячейке B4>80, то в ячейке с приведенной формулой будет записано "Сданы", иначе – "Не сданы".

  =ЕСЛИ(СУММ(А1:А10)>0;СУММ(В1:В10);0).

Если сумма значений в столбце А1:А10 больше 0, то вычислится сумма значений в столбце В1:В10, в противном случае результат – 0.

Дополнительные логические функции

  =И (логич_выр1;логич_выр2)
  =ИЛИ (логич_выр1;логич_выр2)
  =НЕ (логич_выр)

позволяют создавать сложные условия, например:

  =ЕСЛИ (И(СУММ(А1:А10)>0;СУММ(В1:В10)>0);СУММ (A1:B10);0).

Если суммы и в столбце А1:А10 и в столбце В1:В10 положительны, то вычислить суму значений в ячейках А1:В10, иначе – 0.

Статистические функции

MS EXCEL предоставляет широкие возможности для анализа статистических данных. Для решения простых задач можно использовать встроенные функции. Рассмотрим некоторые из них.

  1. Вычисление среднего арифметического последовательности чисел:

=СРЗНАЧ (числа).

Например,

  =СРЗНАЧ(5;7;9);
  =СРЗНАЧ (А1:А10;С1:С10)
  =СРЗНАЧ (А1:Е20).
  1. Нахождение максимального (минимального) значения:

=МАКС (числа)

=МИН (числа).

Например:

    =МАКС (А4:С10);
    =МИН (А2;С4;7).
  1. Вычисление медианы (числа, являющегося серединой множества):

=МЕДИАНА(числа).

  1. Вычисление моды (наиболее часто встречающегося значения в множестве):

=МОДА(числа).

Следующие функции предназначены для анализа выборок генеральной совокупности данных.

  1. Дисперсия:

=ДИСП(числа).

  1. Стандартное отклонение:

=СТАНДОТКЛОН( числа).

Статистический анализ с помощью Пакета анализа

Для решения сложных задач применяется Пакет анализа. Пакет анализа – это дополнение EXCEL, расширяющее его аналитические возможности и позволяющие строить гистограммы, составлять таблицы рангперсентиль, делать случайные или периодические выборки данных и находить их статистические характеристики, генерировать неравномерно распределенные случайные числа, проводить регрессивный анализ и многое другое.

Чтобы воспользоваться инструментами анализа, выполните следующие действия.

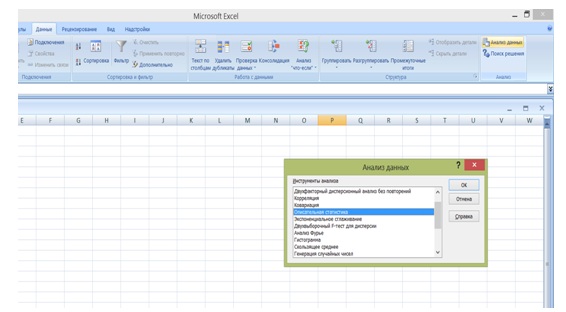
  1. В меню Данные > Анализ выберите команду Анализ данных.
Инструмент Описательная статистика

Рис. 3.5. Инструмент Описательная статистика
  1. Выберите из списка название нужного инструмента анализа и нажмите кнопку ОК.

В большинстве случаев в открывшемся диалоговом окне нужно просто указать интервал исходных данных интервал для вывода результатов и задать некоторые параметры.

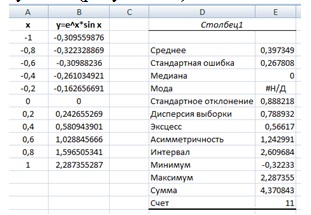
Инструмент Описательная статистика формирует таблицу статистических данных, ускоряя и упрощая этот процесс по сравнению с использованием формул 1- 6 (рис. 3.6 рис. 3.6).

Обработка столбца В инструментом Описательная статистика

Рис. 3.6. Обработка столбца В инструментом Описательная статистика

Инструмент Генерация случайных чисел дает возможность получать равномерное и неравномерное распределение.

Инструмент Гистограмма позволяет создавать гистограммы распределения данных. Область значений измеряемой величины разбивается на несколько интервалов, называемых карманами, в которых в виде столбцов откладывается количество попавших в этот интервал измерений, называемое частотой.

Пример 2. Пусть дана таблица с данными о температуре воздуха в Краснодаре летом 2014г. Интервал изменения температуры от 18 до 38 градуса по Цельсию (его можно определить с помощью функций МАКС() и МИН()).

  1. Разобьем этот интервал на подинтервалы – карманы шириной, например, 2 градуса по Цельсию (ширина карманов не обязательно должна быть равной).
  2. Воспользуемся командой Заполнить из меню Главная в группе Редактирование для быстрого заполнения столбца карманов (значения в столбце будут изменятся от 18 до 38 градусов по Цельсию с шагом 2 градуса).
  3. Выполним команду Анализ данных из меню Данные. В открывшемся диалоговом окне зададим входной интервал (это ячейки с данными о температуре), интервал карманов, выходной интервал (надо указать только верхнюю, левую ячейку для вывода результатов) и установим флажок Вывод графика.
  4. После нажатия кнопки ОК на экран будет выведена гистограмма, а рядом со столбцом карманов появится столбец частот, показывающий, сколько дней летом в Краснодаре имели температуру, попадающую в каждый интервал.

ЗАДАНИЕ

Каждый вариант состоит из двух заданий. Для выполнения первого задания необходимо:

  1. На рабочем листе № 4 построить таблицу значений функции согласно варианта задания и ее график.
  2. Определите среднее, минимальное и максимальное значение функции и вывести эти данные на графике.
  3. Используя логическую формулу, вычислить сумму значений функций, если среднее, минимальное и максимальное значения имеют одинаковые знаки и произведение в противном случае.
  4. Произвольной ячейке присвоить имя и сгенерировать в ней случайное число. В таблице значений функции добавить еще один столбец, полученный умножением у на случайное число. Добавить на графике функции второй график, соответствующий полученному столбцу данных.

Исходными данными для второго задания являются варианты заданий к лабораторной работе № 1. Необходимо:

  1. Провести статистический анализ с использованием функций 1-6 методических указаний к работе.
  2. Провести статистический анализ с использованием инструмента Описательная статистика
  3. Построить гистограмму распределения данных.

Варианты заданий

1 \[ $$Y=e^{x}cos^{2}2x+|x|$$ \] \[ $$-1\leq x \leq 1,5;\Delta x=0,2$$ \]
2 \[ $Y=|x+e^{x}|+tg3x\lg x^{2}$ \] \[ $-10\leq x \leq 10;\Delta x=1$ \]
3 \[ $Y=(x^{3}-cosx^{2})/(e^{4x}-tgx))$ \] \[ $-5\leq x \leq 5;\Delta x=0,75$ \]
4 \[ $Y=(x+4|x|)^{2}+3xsin(|x|)$ \] \[ $-1,5\leq x \leq 5,5;\Delta x=0,2$ \]
5 \[ $Y=xcosx/(|x+e^{x}|tgx)$ \] \[ $-5,2\leq x \leq 1,5;\Delta x=0,7$ \]
6 \[ $Y=lg x^{2}e^{sin2x}/lg(3x)$ \] \[ $1\leq x \leq 100;\Delta x=5$ \]
7 \[ $Y=e^{(x+2)}ln^{2}2x/(x+10e^{x})$ \] \[ $1\leq x \leq 50;\Delta x=2,5$ \]
8 \[ $Y=|sin(2x)+tg(3x)|^{1/2}+e^{4x}$ \] \[ $-2,5\leq x \leq 1,5;\Delta x=0,4$ \]
9 \[ $Y=1-|sin(x)|+e^{(ln(2x)+lg(x))}$ \] \[ $1\leq x \leq 10;\Delta x=0,1$ \]
10 \[ $Y=(-1)^{x}e^{sinx}cosx^{2}$ \] \[ $1\leq x \leq 15;\Delta x=1$ \]
11 \[ $Y=2x+\frac{sin^{2}(x)}{2+x}$ \] \[ $1\leq x \leq 5;\Delta x=0,2$ \]
12 \[ $Y=2ln(1+x^{2})+(1+cos^{4}x)/2+x$ \] \[ $-1\leq x \leq 0;\Delta x=0,05$ \]
13 \[ $Y=\sqrt{1+|2sin(3x)|}^{1/3}$ \] \[ $1\leq x \leq 5;\Delta x=0,2$ \]
14 \[ $Y=(3+sin^{2}(2x))/(1+cos^{2}(x))$ \] \[ $-1,5\leq x \leq 0;\Delta x=0,05$ \]
15 \[ $Y=(1+x)/(1+\sqrt{|x|}e^{-x}+|sin(x)|)$ \] \[ $-1,4\leq x \leq 1,4;\Delta x=0,2$ \]
16 \[ Y=lgx2 sin2x/lg3x$ \] \[ $1\leq x \leq 100;\Delta x=5$ \]
17 \[ $Y=e^{x+2}+ln^{2}(2x)/(x+10e^{x})$ \] \[ $1\leq x \leq 50;\Delta x=2,5$ \]
18 \[ $Y=|sin2x+tg3x|^{1/2}+e^{4x}$ \] \[ $-2,5\leq x \leq 1,5;\Delta x=0,4$ \]
19 \[ $Y=1-|sinx|+ln2x+lgx$ \] \[ $1\leq x \leq 10;\Delta x=0,1$ \]
20 \[ $Y=(-1)^{x}e^{sinx}cosx^{2}$ \] \[ $1\leq x \leq 15;\Delta x=1$ \]

КОНТРОЛЬНЫЕ ВОПРОСЫ

  1. Для чего предназначен Пакет анализа и каков порядок доступа к его инструментам?
  2. В чем заключаются особенности построения гистограммы распределения данных?
  3. Напишите логическую формулу, которая выводит текстовое сообщение "Вычислена сумма" или "Вычислено произведение" в зависимости оттого, что было вычислено на рабочем листе в п.3 задания 1.
  4. Используя информацию о том, что "как правило, 68% данных генеральной совокупности с нормальным распределением находятся в пределах одного стандартного отклонения от среднего значения, а 98% – в пределах двух отклонений", создайте на рабочем листе строку, в которой для задания 1 автоматически будут рассчитываться указанные интервалы.
Next >>
< Lecture 2 || Lecture 3 || Lecture 4 >