Компьютерное моделирование при обработке опытных данных

Сплайн-интерполяция

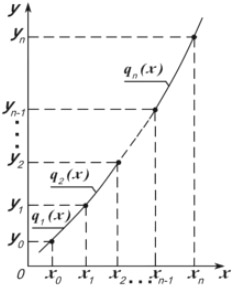
Сплайны стали широко использоваться в вычислительной математике сравнительно недавно. В машиностроительном черчении они применяются уже давно, так как сплайны - это лекала или гибкие линейки, деформация которых позволяет провести кривую через заданные точки (x_i, у_i).

Используя теорию изгиба бруса при малых деформациях, можно показать, что сплайн - это группа кубических многочленов, в местах сопряжения которых первая и вторая производные непрерывны. Такие функции называются кубическими сплайнами. Для их построения необходимо задать коэффициенты, которые единственным образом определяют многочлен в промежутке между данными точками.

Например, для некоторых функций (рис.11.5) необходимо задать все кубические функции q₁(x), q₂(x), :q_n(x).

В наиболее общем случае эти многочлены имеют вид:

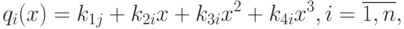
где k_ij - коэффициенты, определяемые описанными ранее условиями, количество которых равно 4n. Для определения коэффициентов k_ij необходимо построить и решить систему порядка 4n.

Рис. 11.5.

Первые 2n условий требуют, чтобы сплайны соприкасались в заданных точках:

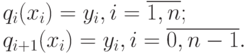
Следующие (2п-2) условий требуют, чтобы в местах соприкосновения сплайнов были равны первые и вторые производные:

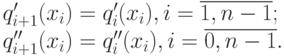
Система алгебраических уравнений имеет решение, если число уравнений соответствует числу неизвестных. Для этого необходимо ввести еще два уравнения. Обычно используются следующие условия:

При построении алгоритма метода первые и вторые производные удобно аппроксимировать разделенными разностями соответствующих порядков.

Полученный таким образом сплайн называется естественным кубическим сплайном. Найдя коэффициенты сплайна, используют эту кусочно-гладкую полиноминальную функцию для представления данных при интерполяции.

Аппроксимация опытных данных

В результате проведения натурного эксперимента получена табличная функция:

где

N-количество узловых точек в таблице,

n=N-1.

Задача аппроксимации заключается в отыскании аналитической зависимости y=f(x) полученной табличной функции.

В настоящее время существует 2 способа аппроксимации опытных данных:

Первый способ. Этот способ требует, чтобы аппроксимирующая кривая F(x), аналитический вид которой необходимо найти, проходила через все узловые точки таблицы. Эту задачу можно решить с помощью построения интерполяционного многочлена степени n:

( 11.12)

Однако этот способ аппроксимации опытных данных имеет недостатки:

1. Точность аппроксимации гарантируется в небольшом интервале [x₀, x_n] при количестве узловых точек не более 7-8.
2. Значения табличной функции в узловых точках должны быть заданы с большой точностью.

Известно, что как бы точно не проводился эксперимент, результаты эксперимента содержат погрешности. Дело в том, что на самом деле исследуемая величина зависит не только от одного аргумента Х, но и от других случайных факторов, которые от опыта к опыту колеблются по своим собственным случайным законам. Этим самым обуславливается случайная колеблемость исследуемой функции.

В результате аппроксимировать опытные данные с помощью интерполяционного многочлена, который проходил бы через все узловые точки таблицы, не всегда удается. Более того, стремясь пройти через все узловые точки таблицы и увеличивая порядок многочлена, мы тем самым начинаем воспроизводить не только закономерные изменения снимаемой функции, но и ее случайные помехи.

Второй способ. На практике нашел применение другой способ аппроксимации опытных данных - сглаживание опытных данных. Сущность этого метода состоит в том, что табличные данные аппроксимируют кривой F(x), которая не обязательно должна пройти через все узловые точки, а должна как бы сгладить все случайные помехи табличной функции.