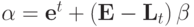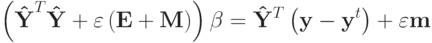Нейроинформатика
[+]
Опубликован: 01.03.2007 | Доступ: свободный | Студентов: 1638 / 246 | Оценка: 4.58 / 4.39 | Длительность: 20:15:00
Тема: Искусственный интеллект и робототехника
Специальности: Программист
Теги: алгоритмы, выходной нейрон, вычисления, искусственная жизнь, исследования, кластеры, компоненты, линейное пространство, моделирование, нейрокомпьютер, нейронные сети, нелинейный преобразователь, обучающая выборка, обучение, обучение нейронной сети, ошибка обучения, поиск, программирование, сеть встречного распространения, сеть хопфилда, синапс, тестирование, элементы
Лекция 7:

Скрытые параметры и транспонированная регрессия
A
|
версия для печати
< Лекция 6 || Лекция 7: 123456 || Лекция 8 >

Если в качестве искомой формулы рассматривать линейную комбинацию векторов опорной группы, то требуемой инвариантности можно достичь, наложив некоторое условие на коэффициенты разложения. Таковым условием является равенство суммы коэффициентов единице:

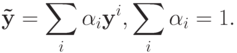
{\bf{\tilde y}}= \sum\limits_i {\alpha_i {\bf{y}}^i }, \sum\limits_i {\alpha_i }= 1 .

Для нелинейной регрессии естественно использовать однородные рациональные функции [7.2].

Рассматривались два вида решения. Первый:

{\bf{\tilde y}}= {\bf{m}}_{\bf{y}}+ \sum\limits_{i = 1}^q {\beta_i \left( {{\bf{y}}^i - {\bf{m}}_{\bf{y}}}\right)}{, } {\alpha_I}= \beta_i + \frac{1}{q}- \frac{1}{q}\sum\limits_{k = 1}^q {\beta_k } ( 2)

где {\bf{\tilde y}} - восстановленный вектор свойств, yi - вектор свойств i -го объекта опорной группы, q - мощность опорной группы,

{\bf{m}}_{\bf{y}}= \frac{1}{q}\sum\limits_{i = 1}^q {{\bf{y}}^i }.
- среднее значение.

Во втором случае в качестве {\bf{m}}_{\bf{y}}, выбирался один из векторов опорной группы.

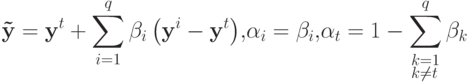{\bf{\tilde y}}= {\bf{y}}^t + \sum\limits_{i = 1}^q {\beta_i \left( {{\bf{y}}^i - {\bf{y}}^t }\right)}{, } {\alpha_i }= {\beta_i }{, } {\alpha_t}= 1 - \sum\limits_{\scriptstyle k = 1 \hfill \atop \scriptstyle k \ne t \hfill}^q {\beta_k } ( 3)

Заметим, что легко построить нейронную сеть, вычисляющую такие формулы [7.5, 7.6].

Из-за предположения о малости опорной группы объектов в качестве одного из путей решения предлагается перебор всех наборов заданного размера. Было предложено искать минимум одного из двух критериев:

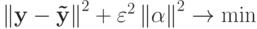  • \left\| {{\bf{y}}- {\bf{\tilde y}}}\right\|^2 + \varepsilon^2 \left\| \alpha \right\|^2 \to \min.
  • \left\| {{\bf{y}}- {\bf{\tilde y}}}\right\| + \varepsilon \left\| \alpha \right\| \to \min.

В случае а) точное решение находится из системы линейных уравнений. Введем обозначения:

  • Y - матрица векторов опорной группы, n строк, q столбцов. n - число известных компонент восстанавливаемого вектора y.
  • {\bf{\hat Y}}{\rm{= (y}}^i {\rm{- m}}_{\rm{y}}{\rm{) }} - матрица Y в которой из каждого столбца вычтен вектор my ( yt в случае 2).
  • M - матрица, все элементы которой равны 1,
  • m - вектор, все компоненты которого равны 1,
  • E - единичная матрица,
  • \alpha {\rm{,}}\beta - вектора размерностью q.

Для выражения (2)

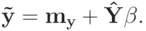
{\bf{\tilde y}}= {\bf{m}}_{\bf{y}}+ {\bf{\hat Y}}\beta .
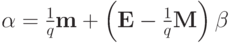\alpha = \frac{1}{q}{\bf{m}}+ \left( {{\bf{E}}- \frac{1}{q}{\bf{M}}}\right)\beta.

Дифференцируя выражение а) и приравнивая нулю, получаем:

\left( {{\bf{\hat Y}}^T {\bf{\hat Y}}+ \varepsilon \left( {{\bf{E}}- \frac{1}{q}{\bf{M}}}\right)}\right)\beta = {\bf{\hat Y}}^T \left( {{\bf{y}}- {\bf{m}}_{\bf{y}}}\right) .

Для выражения (3),

et - вектор, t -ая компонента которого равна 1, остальные 0.

Lt = (et) - матрица, столбцы которой равны вектору et.

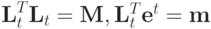
{\bf{L}}_t^T {\bf{L}}_t = {\bf{M}}, {\bf{L}}_t^T {\bf{e}}^t = {\bf{m}}

Имеем

{\bf{\tilde y}}= {\bf{y}}^t + {\bf{\hat Y}}\beta .
\alpha = {\bf{e}}^t + \left( {{\bf{E}}- {\bf{L}}_t }\right)\beta

\left( {{\bf{\hat Y}}^T {\bf{\hat Y}}+ \varepsilon \left( {{\bf{E}}+ {\bf{M}}}\right)}\right)\beta = {\bf{\hat Y}}^T \left( {{\bf{y}}- {\bf{y}}^t }\right) + \varepsilon {\bf{m}}

Дальше >>
< Лекция 6 || Лекция 7: 123456 || Лекция 8 >

Вопросы и ответы

вопросов: 0