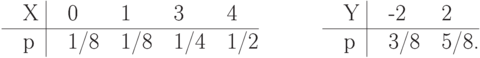Базовые понятия теории информации
Рассмотрим более простой пример.
Пусть дискретная случайная величина  равна количеству очков, выпавших на игральной
кости, а дискретная случайная величина
равна количеству очков, выпавших на игральной
кости, а дискретная случайная величина  равна 0, если выпавшее количество очков нечетно, и 1,
если выпавшее количество очков четно. Найти
равна 0, если выпавшее количество очков нечетно, и 1,
если выпавшее количество очков четно. Найти 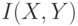 и
и 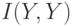 .
.
Составим законы распределения вероятностей дискретной случайной величины  и
и  .
.
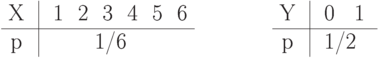
Таким образом, при 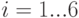
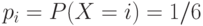 и,
соответственно, при
и,
соответственно, при 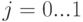
 .
.
Составим также закон совместного распределения вероятностей этих дискретных случайных величин
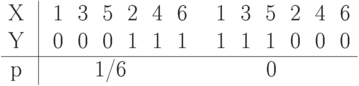
Таким образом,
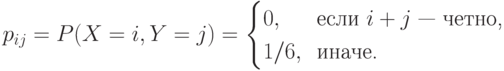
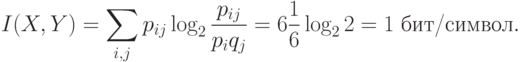
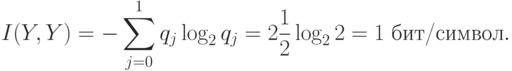
Точное количество выпавших очков дает точную информацию о четности, т.е.
1бит. Из 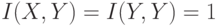 бит/сим и 3-го свойства информации
следует, что информация об
бит/сим и 3-го свойства информации
следует, что информация об  полностью определяет
полностью определяет  , но не
наоборот, т.к.
, но не
наоборот, т.к. 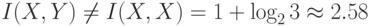 бит/сим.
Действительно,
бит/сим.
Действительно,  функционально зависит от
функционально зависит от  , а
, а  от
от  функционально не зависит.
функционально не зависит.
Расчеты через энтропию будут следующими
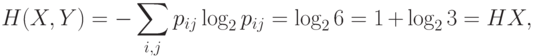
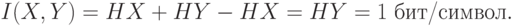
Упражнение 5
Найти энтропию дискретной случайной величины  , заданной распределением
, заданной распределением
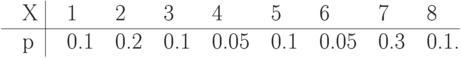
Упражнение 6
Значения дискретной случайной величины  и
и  определяются подбрасыванием
двух идеальных монет, а дискретная случайная величина
определяются подбрасыванием
двух идеальных монет, а дискретная случайная величина  равна сумме количества "гербов", выпавших при
подбрасывании этих монет. Сколько информации об
равна сумме количества "гербов", выпавших при
подбрасывании этих монет. Сколько информации об  содержится в
содержится в  ?
?
Упражнение 7
Сколько информации об  содержится в дискретной случайной величине
содержится в дискретной случайной величине  ,
где независимые дискретные случайные величины
,
где независимые дискретные случайные величины  и
и  могут с
равной вероятностью принимать значение либо 0, либо 1? Найти
могут с
равной вероятностью принимать значение либо 0, либо 1? Найти 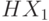 и
и 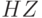 .
Каков характер зависимости между
.
Каков характер зависимости между  и
и  ?
?
Упражнение 8
Дискретные случайные величины  ,
,  - зависимы и распределены также как
и соответствующие дискретные случайные величины из предыдущей задачи. Найти
- зависимы и распределены также как
и соответствующие дискретные случайные величины из предыдущей задачи. Найти 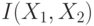 ,
если совместное распределение вероятностей
,
если совместное распределение вероятностей  и
и  описывается законом
описывается законом
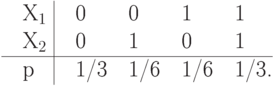
Упражнение 9
Дискретные случайные величины  и
и  определяются подбрасыванием двух
идеальных тетраэдров, грани которых помечены числами от 1 до 4. дискретная случайная величина
определяются подбрасыванием двух
идеальных тетраэдров, грани которых помечены числами от 1 до 4. дискретная случайная величина  равна сумме чисел, выпавших при подбрасывании этих тетраэдров, т.е.
равна сумме чисел, выпавших при подбрасывании этих тетраэдров, т.е.  .
Вычислить
.
Вычислить  ,
, 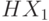 и
и 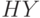 .
.
Упражнение 10
Подсчитать сколько информации об  содержится в дискретной случайной величине
содержится в дискретной случайной величине 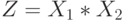 , а также
, а также 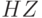 . Дискретные случайные величины
. Дискретные случайные величины  и
и  берутся из
предыдущего упражнения.
берутся из
предыдущего упражнения.
Упражнение 11
Дискретная случайная величина  может принимать три значения
может принимать три значения  , 0 и 1 с
равными вероятностями. Дискретная случайная величина
, 0 и 1 с
равными вероятностями. Дискретная случайная величина  с равными вероятностями может принимать
значения 0, 1 и 2.
с равными вероятностями может принимать
значения 0, 1 и 2.  и
и  - независимы.
- независимы. 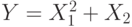 . Найти
. Найти  ,
, 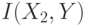 ,
, 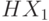 ,
, 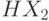 ,
, 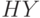 .
.
Упражнение 12
Найти энтропии дискретных случайных величин  ,
,  ,
,  и
количество информации, содержащейся в
и
количество информации, содержащейся в 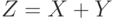 относительно
относительно  .
.  и
и  - независимы и задаются распределениями
- независимы и задаются распределениями