Нейросетевые модели пошаговой оптимизации, маршрутизации и тактических игр
Будут игры беспредельные,
В упоительности цельные...
К. Бальмонт. "Будут игры беспредельные..."
Логическая нейронная сеть - средство пошагового принятия решений
Задачи пошаговой оптимизации составляют широкий класс задач исследования операций. Это - многочисленные задачи нахождения оптимальных стратегий управления, таких, как вывод космического объекта в заданную точку, минимизация длины пути следования в транспортной сети и др.
Однако высокая сложность задач указанного типа выдвигает проблему запоминания и использования опыта, т.е. применения элементов обучения.
При решении задач оперативного управления и планирования, по-видимому, нецелесообразно каждый раз, например, прокладывать маршрут следования груза по железной дороге с учётом огромного числа динамически возникающих факторов. Конечно, пользуются простыми эвристическими алгоритмами управления, достаточно детализированными и децентрализованными для возможности учёта постоянно изменяющихся условий и обстановки.
В то же время, пошаговая оптимизация примитивно вырождается в последовательно принимаемое решение вида: "я нахожусь в состоянии Х; куда двигаться (что делать) дальше для достижения минимума (максимума) целевой функции?" Такая простая схема движения к оптимуму и порождает возможность априорного расчёта оптимальных стратегий пошагового изменения состояния системы для того, чтобы в рабочем режиме по функции цели и по текущему состоянию системы находить запомнившийся предпочтительный переход в соседнее состояние, уменьшающий значение этой функции.
Такая схема соответствует и идее ситуационного управления, и рассмотренной ранее схеме нейросетевой реализации управления.
К стратегии пошаговой оптимизации следует отнести и тактические игры, заключающиеся в последовательном выполнении противниками (преимущественно, двумя) действий, приводящих к минимизации некоторой целевой функции, например, функции потерь. Здесь перед отдельным игроком стоит проблема выбора наилучшего хода для сложившейся ситуации.
Для этого, несомненно, могут каждый раз рассчитываться все возможные варианты ходов с возможными ответными ходами. Может быть использован и теоретический опыт. Однако такой анализ требует огромной производительности вычислительных средств. Он недостаточно оперативен.
Здесь решение находится на основе анализа действий опытного игрока, помнящего эффективный выход из множества сложившихся ситуаций и эксплуатирующего свои способности ассоциативного мышления. Используется и коллективный опыт, теоретически обобщённый.
Автоматизация подобного анализа может быть произведена на основе разработки "подсказчика", хранящего в памяти большое количество ситуаций и рекомендующего следующий ход в соответствии с опытом экспертов, с историей и с теоретическим анализом.
Всё сказанное выше определяет целесообразность применения логической нейронной сети.
Нейросетевая транспортная модель динамической маршрутизации
- Вперёд! - скомандовал сам себе бравый солдат Швейк. - Долг зовёт. Я должен попасть в Будейовицы.
Но по несчастной случайности, вместо того чтобы идти от Противина на юг - к Будейовицам, стопы Швейка направились на север - к Писеку.
Я. Гашек. Похождения бравого солдата Швейка
Транспортная сеть представляет собой конечное множество пунктов (узлов), соединённых между собой линиями связи. Ограничения на топологию связей отсутствуют.
Случайным образом или по некоторому закону (например, по расписанию) в сети возникают заявки на транспортное перемещение, на передачу сообщений или, в общем случае, - на движение объекта из пункта отправления к пункту назначения. Такими пунктами может быть любая пара пунктов сети. Заявки требуют прокладки маршрутов следования. Маршрут может учитывать как непосредственное перемещение из пункта отправления в пункт назначения (если существует связь), так и транзитное перемещение через промежуточные пункты.
При моделировании целесообразно наблюдать единичный акт перемещения по каждому маршруту: из одного пункта в другой. Это позволяет применять динамическое управление реализацией маршрута и, в зависимости от меняющейся обстановки, адаптивно изменять маршрут при движении от пункта отправления к пункту назначения.
Модель ориентирована на решение задачи "проникновения" из пункта отправления в пункт назначения кратчайшим или менее загруженным доступным путём, т.е. за минимально возможное время, а также на повышение пропускной способности сети и вероятности успешного завершения маршрута. Решение этой задачи характерно для маршрутизации в компьютерной сети, включая Интернет, для почтовой связи, оптимизации грузовых перевозок всех видов, нефтяных и газовых магистралей и др. В то же время с помощью этой модели может быть составлено оптимальное транспортное расписание, например, движения поездов.
Рассмотрим "большие" транспортные сети, покрывающие значительные территории крупных государств или их ассоциаций. Для проекции сети на плоскость введём систему координат (х, у), позволяющую однозначно идентифицировать (адресовать) не только каждый из N пунктов сети, но и приблизительное направление движения. Координаты могут быть декартовыми, географическими и др. Координаты достаточно определять приблизительно.
Следующие построения произведём для каждого пункта сети, на котором решается задача смещения транспорта, находящегося в этом пункте, в смежный пункт для достижения конечной цели.
Пусть 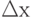 - разность координаты х пункта назначения и пункта текущего нахождения транспорта, из которого следует произвести шаг перемещения - смещение;
- разность координаты х пункта назначения и пункта текущего нахождения транспорта, из которого следует произвести шаг перемещения - смещение; 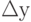 - аналогичная разность координаты у.
- аналогичная разность координаты у.
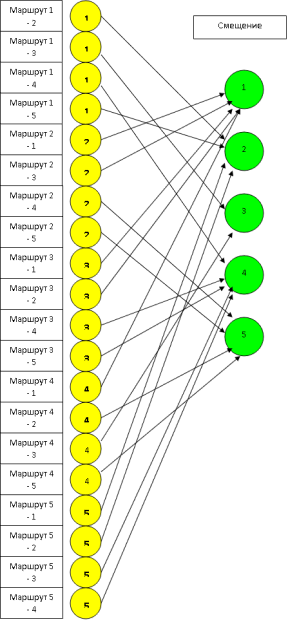
Для нахождения пункта смещения достаточно использовать однослойную логическую нейронную сеть (рис. 17.1). Она строится следующим образом.
Разобьём весь интервал изменения 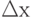 для данной транспортной сети на отрезки а1, ..., ат. За каждым отрезком закрепим нейрон рецепторного слоя. Возбуждение этого нейрона определяется достоверностью принадлежности найденного текущего значения
для данной транспортной сети на отрезки а1, ..., ат. За каждым отрезком закрепим нейрон рецепторного слоя. Возбуждение этого нейрона определяется достоверностью принадлежности найденного текущего значения 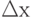 соответствующему отрезку.
соответствующему отрезку.
Весь интервал возможного изменения 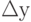 также разобьём на отрезки b1, ..., bn. За каждым отрезком закрепим нейрон-рецептор. Его возбуждение определяется достоверностью того, что текущее значение
также разобьём на отрезки b1, ..., bn. За каждым отрезком закрепим нейрон-рецептор. Его возбуждение определяется достоверностью того, что текущее значение 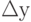 принадлежит соответствующему отрезку.
принадлежит соответствующему отрезку.
Закрепим N рецепторов за пунктами сети. Возбуждение этих рецепторов определяет пункт нахождения (отправления) или промежуточный пункт, из которого следует произвести смещение.
Выходной слой состоит из N нейронов. Их возбуждение определяет пункты, в которые необходимо или возможно произвести смещение.
Рекомендация по смещению не обязательно однозначна. Могут выдаваться варианты смещения, которые подлежат дополнительному анализу с учётом различных динамических факторов.
Синапсические связи вводятся так, чтобы каждое единичное возбуждение рецепторов всех элементов тройки {ai, bj, <k-й пункт нахождения>} приводил к максимальному возбуждению нейрона выходного слоя, называющего пункт дальнейшего смещения.
Целесообразно выбрать следующую функцию активации i-го нейрона:
 , где знаком
, где знаком  обозначают замену отрицательных значений нулём, т.е.
обозначают замену отрицательных значений нулём, т.е.
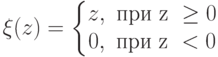
Таким образом, первоначально по разностям координат х и у пункта отправления и пункта назначения отыскивается промежуточный пункт смещения. Для продолжения имитации движения возбуждается рецептор, соответствующий найденному пункту смещения, для которого вновь определяются 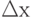 и
и 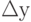 по отношению к пункту назначения. Возбуждаются соответствующие этим разностям рецепторы, и для данного пункта нахождения вновь по максимальному возбуждению нейрона выходного слоя определяется следующий пункт смещения и т.д.
по отношению к пункту назначения. Возбуждаются соответствующие этим разностям рецепторы, и для данного пункта нахождения вновь по максимальному возбуждению нейрона выходного слоя определяется следующий пункт смещения и т.д.
Здесь предполагается, что весь маршрут сопровождается с некоторого центрального пункта, где находится логическая нейронная сеть. Однако упрощённая нейронная сеть может быть составлена для каждого узла отдельно. Тогда, при нахождении пункта смещения, используется подобная логическая нейронная сеть, находящаяся на нём. Таким образом, пункты "передают" друг другу движущийся транспорт, пока он не достигнет пункта назначения.
Применение координат целесообразно для "больших" транспортных сетей, содержащих тысячи и десятки тысяч пунктов, например, для территории России. Тогда координаты могут указывать на некоторый условный центр подсети, объединяющей несколько пунктов. Например, поездка осуществляется в район Архангельска, в район Бухары и т.д.
При небольшом количестве пунктов в транспортной сети логическая нейронная сеть может быть построена способом, рассмотренным в следующем примере.
Пример.
Пусть транспортная сеть представлена на рис. 17.2.
Тогда логическая нейронная сеть, с помощью которой производится имитация движения транспорта, имеет вид на рис. 17.3.
Ниже будет рассмотрена возможность введения обратных связей, позволяющих ввести элементы адаптивного динамического управления движением, подобно рассмотренным для беспроводных телекоммуникационных сетей.
Движение транспорта с выбором альтернативного пункта смещения
Итак, мы рассматриваем случай, когда любой маршрут следования из пункта отправления к пункту назначения осуществляется с помощью последовательности смещений между смежными пунктами. Так что маршрут не формируется весь заранее, а реализуется динамически с учётом приоритетного обращения к смежным пунктам и загрузки этих пунктов. Это позволяет производить адаптацию реального маршрута к текущей загрузке транспортной сети так же, как это было рассмотрено для сети телекоммуникационной.
Предположим, что для каждого пункта назначения на каждом пункте хранятся приоритетные веса смежных пунктов смещения для достижения цели с максимальным качеством – минимум расстояния, минимум времени, минимум опасности циклического движения и др. Для всех возможных пунктов назначения данная информация объединяется в таблицу.
Пусть смежными для данного пункта являются пункты B1, ..., BN. Тогда для отдельного адреса назначения А указанная информация может иметь вид строки в таблице:
Если в строке указан не единственный вес, отличный от нуля, то этим определяется возможность альтернативного смещения. В этом случае общую маршрутизацию, осуществляемую в сети, следует назвать свободной. Если в строке декларируется единственная единица, то альтернативы не существует. Маршрутизацию, где все смещения для достижения пунктов назначения определены однозначно, следует назвать жёсткой.
Например, при движении из пункта 1 (рис. 17.2) в пункт 5 и при обоснованном назначении весов смещения, подобная строка может иметь следующий вид:
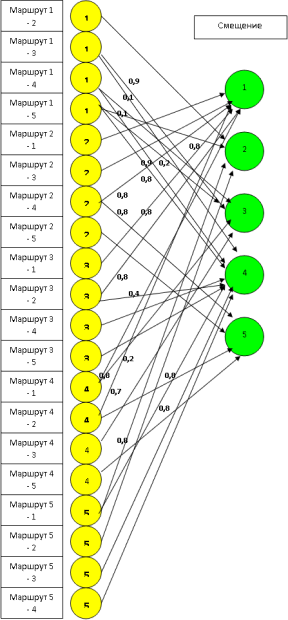
С учётом альтернативных смещений и их весов, логическая нейронная сеть для рассматриваемого примера может быть приведена к виду, представленному на рис. 17.4. Единичные веса связей не обозначены, а альтернативные веса выбраны примерно. Чтобы не загружать рисунок, представлены не все возможные альтернативные решения.
Альтернативное смещение в смежный пункт реализует элемент самоуправления, адаптации на основе обратной связи, ведущей от смежных пунктов к пункту текущего нахождения транспорта.
Каждый пункт (узел) сети характеризуется своей максимальной пропускной способностью и её текущим резервом - для нахождения пункта смещения. Тогда, логическая нейронная сеть, находящаяся на каждом пункте, имеет отрицательные веса связей, ведущих от буферов смежных узлов.
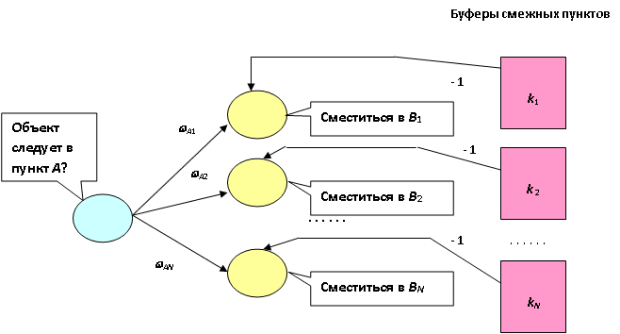
На рисунке 17.5 представлен фрагмент логической нейронной сети, находящейся на каждом узле, в котором отображён выбор смежного пункта смещения при следовании объекта в пункт А.
Функция активации:

В данном случае эта функция имеет вид:
 , если эта разность превышает порог h, 0 в противном случае. Здесь ki – коэффициент загрузки i-го пункта смещения.
, если эта разность превышает порог h, 0 в противном случае. Здесь ki – коэффициент загрузки i-го пункта смещения.
Порог h выбирается экспериментально так, чтобы предпочтение могло быть выбрано между не полностью загруженными узлами.
В построенной обобщённой модели движения в транспортной сети буфер отображает пропускную способность узла. Конкретно это может быть: количество путей железнодорожной станции, количество взлётно-посадочных полос, максимальное использование радио каналов и т.д. В рамках теории логических нейронных сетей значение коэффициента загрузки буфера можно интерпретировать как достоверность высказывания о том, что буфер заполнен полностью.
Принятую дисциплину использования загрузки буфера для разрешения движения в сторону узла также следует считать достаточно общей: ведь если мы узнаём, что на некотором участке дороги создалась "пробка", то разумно не надеяться на то, что к нашему приезду она рассосётся. Следует изменить маршрут. Такова практика организации полётов и передачи информационных пакетов. Ведь следует учесть, что прогнозирование ситуации на узле на тот момент, когда поезд до него доберётся, требует согласованного анализа многих маршрутов. Это значительно усложняет динамическое управление движением. Проще запретить движение в сторону перегруженного узла.
Моделирование совместного движения множества объектов в транспортной сети по испытываемым сценариям необходимо, прежде всего, для выделения маршрутов (поездов, самолётов, информационных пакетов и др.) при поиске оптимальных расписаний движения. В частности, такое моделирование предполагается в рамках общей методики оптимального обслуживания пассажиропотоков.
Нейросетевой "подсказчик" в тактической игре
Остап ... подошёл к одноглазому, сидевшему за
первой доской, и передвинул королевскую пешку с
клетки e2 на клетку е4.
И. Ильф, Е. Петров. Двенадцать стульев
Схема пошаговой оптимизации наилучшим образом ложится на схему игры, где последовательные действия одного или нескольких игроков приводят к успеху, обусловленному правилами.
Единичное действие, чаще всего называемое ходом, должно либо статистически, либо комбинационно приводить к увеличению "качества" или к уменьшению "штрафа" на пути к победе (или к поражению). И здесь большое значение имеет не только длительный анализ всех возможных продолжений, грозящий цейтнотом, но и огромный опыт и фактические знания, переродившиеся в интуицию и позволяющие действовать механически в условиях блиц-турнира. Следовательно, должны быть реализованы механизмы запоминания и извлечения опыта и знаний в пошаговых действиях. Основным средством такой реализации является нейросеть - как природная, так и искусственная.
Рассмотрим игру в шахматы. Аналогом пункта в транспортной сети здесь является позиция на шахматной доске, состоящей из 64 клеток. Каждая клетка может быть пустой или иметь значение символа занимаемой фигуры.
То есть, каждая клетка i может принимать значение из множества { }. При этом позиции являются симметричными относительно цвета фигур. Игроку, прибегающему к услугам "подсказчика", главное - указать: "фигуры мои - фигуры противника". Играть можно "самому с собой", как бы поворачивая доску после очередного хода. (Если "подсказчик" играет сам с собой, логично предположить, что такая игра всегда будет сводиться к ничьей?)
}. При этом позиции являются симметричными относительно цвета фигур. Игроку, прибегающему к услугам "подсказчика", главное - указать: "фигуры мои - фигуры противника". Играть можно "самому с собой", как бы поворачивая доску после очередного хода. (Если "подсказчик" играет сам с собой, логично предположить, что такая игра всегда будет сводиться к ничьей?)
Тогда рецепторный слой однослойной логической нейронной сети должен состоять (рис. 17.6) из 64 групп нейронов.
Каждая группа закреплена за одной клеткой и, в свою очередь, состоит из 13 нейронов-рецепторов. Каждый рецептор закреплён за одним из возможных значений клетки.
Ясно, что в подавляющем числе случаев значение клетки достаточно задавать с помощью единичного значения возбуждения единственного рецептора из тринадцати, соответствующих этой клетке. Так можно задавать позицию для нахождения следующего хода. Однако можно предусмотреть и неполную, предполагаемую с некоторой достоверностью информацию о значении клетки. Это справедливо, например, для случая игры "вслепую", тем более в сеансе одновременной игры, когда детали ситуации на отдельной доске могут быть забыты.
Целесообразно использовать приведённую в разделе 6.2 функцию активации с единичными синапсическими весами. Значения порогов несущественны; они могут быть положены равными нулю.
Комбинации возбуждения рецепторов должны приводить, в соответствии с непосредственными связями, к максимальному значению возбуждения того нейрона выходного слоя, с которым связан текст - рекомендация следующего хода. Текст может включать исторические ссылки, комментарии, мультимедийные эффекты и др.
Как говорилось, возможно попеременное обращение игроков к нейросети-"подсказчику". Тогда все нечётные обращения соответствуют белым, чёрные - чёрным. Однако интереснее игра живого шахматиста с компьютером.
Конечно, анализ колоссального опыта гроссмейстеров и литературы по теории шахмат не способен по всем возможным ситуациям и для белых, и (симметрично) для чёрных определить абсолютно правильные ходы.
Да и объём информации колоссален! Некоторые шахматные позиции останутся без рекомендаций. Здесь необходимо исследовать, насколько указание нейрона, наиболее возбудившегося, может быть принято в качестве совета, - то есть, насколько это хотя бы статистически соответствует правильному решению или, по крайней мере, не приводит к снижению качества. Следует ли "учить" нейросеть решению по данной комбинации или достаточно использовать её способности ассоциативного мышления?
На этом пути может производиться совершенствование "подсказчика", что повышает интерес игры человека с машиной.
В перспективе своих самостоятельных исследований составьте модель программы игры в "крестики – нолики", первоначально ограничившись попыткой сведения игры "в ничью". Начните разработку модели с анализа возможных ходов противника и с выбора предпочтительного ответа. Для этого заведите три строки, каждая из которых содержит три позиции. В текущем состоянии игры позиция может содержать "крестик" (противника), "нолик" (Ваш) или быть свободной. Несомненно, "традиционный" программный, последовательный анализ каждой позиции всех строк трудоёмок и долог. Ассоциативный принцип "работы" нейронной сети (рис. 17.7) позволяет приблизить его к ассоциативному мышлению игрока и сделать игровую нейрокомпьютерную приставку к персональному компьютеру.
Краткие итоги
- В условиях динамически меняющейся ситуации решение по минимизации некоторой целевой функции приходится принимать по шагам. Это характерно для задач оперативного планирования, при организации движения многих объектов в транспортной сети (при разделении её ресурсов), при многонаправленной одновременной передаче информационных пакетов, в тактических игровых задачах и др.
- При выборе стратегии поведения на каждом шаге целесообразно использовать опыт, зафиксированный в базе знаний и записанный в виде логической нейронной сети.
- В транспортных задачах целесообразно находить смещение в смежный узел по разности координат пункта назначения и пункта текущего нахождения.
- Возможна организация альтернативного смещения в зависимости от загрузки смежных узлов.
- Моделирование движения в сети необходимо для составления оптимальных расписаний движения поездов, полётов и пр..
- На основе логических нейронных сетей могут строиться подсказчики в тактических играх.
Вопросы
- Когда возникает необходимость в пошаговом принятии решений?
- Какие факторы порождают неопределённость при совместном движении многих объектов в транспортной сети?
- Как строится логическая нейронная сеть для нахождения пункта смещения при следовании объекта к конечному пункту?
- Как производится альтернативное смещение в смежный узел в зависимости от текущей загрузки этих узлов?
- В чём заключается идея подсказчика в тактической игре?