Рейтинговые системы на логических нейронных сетях
Стыдно быть бедным, и занимать низкое положение,
когда в государстве царит закон;
равно стыдно быть богатым и знатным,
когда в государстве царит беззаконие.
Конфуций
Структура нейросети и способы обучения
Для определённости, доходчивости и общности построений рассмотрим систему банковского мониторинга, достаточно отображённую в литературе. В [22] при построении программного приложения для решения этой задачи предлагается использовать Карты Кохонена. В них применяется "классическая" нейронная сеть, в которой удалось использовать только семь показателей: собственный капитал, сальдированные активы, ликвидные активы, обязательства до востребования, вклады населения, коэффициент ликвидности, бюджетные средства. Фантазируя, можно развить этот ряд показателей. Ими могут быть: объём инвестиций в развивающуюся экономику, объём прибыли, прошлый рейтинг и значение его дрейфа, отчисления в фонд поддержки науки и образования, налоговые отчисления, отчисления в пенсионный фонд, отчисления в благотворительный и культурный фонд, участие в программах ЮНЕСКО и т.д.
Возможны два способа мониторинга банков.
Первый способ предполагает наличие нескольких банков-эталонов, для которых известны их показатели и значения рейтинга, определённые экспертами. На экране создаются концентрические области одинакового рейтинга, занимаемые точками – образами банков-эталонов. По показателям (возможно, нечётким) анализируемого банка методом ассоциативного поиска по близости к известным точкам находится область рейтинга, которой он принадлежит. В этом случае логическая нейронная сеть отражает связь банков-эталонов с их образами – точками, расположенными в рейтинговых областях. Важно, что эти точки в рейтинговой области выбираются произвольно, рассредоточено.
Второй способ применяется, если известны значимые области изменения показателей, по принадлежности к которым в совокупности банку может быть присвоен тот или иной рейтинг. В этом случае логические функции, лежащие в основе мониторинга, связывают конъюнкции логических значений (возможно объединение некоторых из них операцией дизъюнкции, если это не приводит к противоречию) принадлежности показателей определённым диапазонам, со значением рейтинга. Показатели анализируемого банка могут быть предполагаемыми, неточными.
Напоминаем, что в обоих случаях нейронная сеть является однослойной, содержащей входной слой рецепторов и выходной слой, указывающий на значение координат или рейтинга. Выходной слой должен указывать не только на рейтинг, но и выдавать экспертные рекомендации, а также другие решения и выводы. Таким образом, нейроны своим возбуждением указывают на некоторые тексты, выдаваемые пользователю.
Целесообразен простейший вид обучения (т.е. построения базы знаний, какой является сеть), определяемый концепцией создания нейросети "под задачу". Он заключается в непосредственном введении связей оператором-исследователем "вручную" — от рецепторов к нейронам выходного слоя в соответствии с причинно-следственными связями. Связи отображаются в матрице следования. Таким образом, сеть создаётся уже обученной, готовой к развитию. Её функция активации достаточно проста. Её главная составляющая основана на суммировании величин возбуждения на входе i-го нейрона, умноженных на вес связи. Для реализации первого способа используем функцию активации:
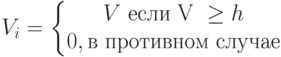
Здесь Vi – искомая величина возбуждения i-го нейрона, Vj – величина возбуждения j-го нейрона (в данном случае - рецептора), связанного с i-м,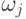 
– вес этой связи. (Значение j "пробегает" по всем нейронам-рецепторам, связанным с данным так, что значение V, в соответствии с известной формулой нахождения математического ожидания, определяет среднюю величину сигнала, поступившего на i-й нейрон.)
Применение весов позволяет пользователю в разной степени оперативно учитывать и изменять влияние различных показателей в процессе эксплуатации.
Порог h выбирается экспериментально для подавления слабых возбуждений и упрощения дальнейшей обработки результатов при включении логической нейронной сети в длинные логические цепочки.
Применение матрицы следования позволяет оперативно вносить изменения и уточнения оператором-экспертом-пользователем, развивать сеть, вводя новые показатели (факторы), изменять веса на основе опыта, изменять тексты принимаемых решений.
Структура экрана рецепторов
Могут использоваться два подхода к организации интерфейса: для пользователя, которому важно научиться лишь нажимать нужные кнопки, и для пользователя-оператора, творчески ведущего и развивающего СПР.
При первом подходе экран рецепторов может быть, например, таким, как показан на рис. 11.1.
Основную часть его составляет "окно прокрутки", через которое можно просматривать и задавать состояние рецепторного слоя, несомненно, не способного поместиться на статическом экране.
В "окне прокрутки" указаны показатели и их оценочные значения (в диапазоне [0, 1]), задаваемые соответствующим рецепторам. Эти значения — вероятностные, по достоверности, интуитивные, экспертные. Они могут предполагать охват нескольких рецепторов. Например, оценка того, что собственный капитал составляет не то 24, не то 34, не то 42 тыс. у. е., но скорее, всё-таки, 24, может привести к приблизительной оценке задаваемых величин возбуждения, равных 0,6, 0,2 и 0,2 (в сумме равных единице) соответственно рецепторов, "отвечающих" за диапазоны (20 - 25], (30 - 35], (40 - 45].
На экране отображены задаваемые без прокрутки показатели, такие, как рейтинг в результате прошлых измерений, выборочные "прошлые" показатели, а также показатели политической, социальной и экономической конъюнктуры. (Их обилие и развитие могут всё-таки потребовать прокрутки.)
Должно быть отображено управление прокруткой, а также меню основных действий. Эти действия следующие: переход на экран выходного слоя, статистическая обработка результатов (предполагает переход к экрану выходного слоя), введение новой связи, введение нового рецептора, изменение веса связи, введение нового нейрона выходного слоя.
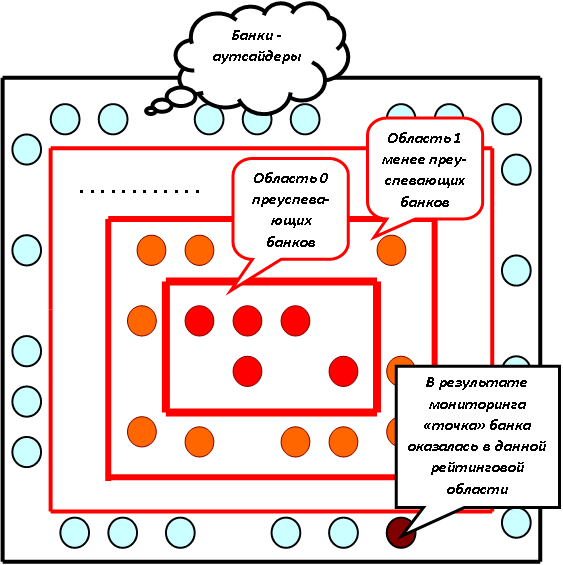
Структура экрана выходного слоя, отображающего рейтинг банков - эталонов
Экран выходного слоя (рис. 11.2) может отображать систему вложенных прямоугольников или других плоских фигур, отражающих распространение рейтинга по убыванию. В центре экрана яркими точками отражены самые преуспевающие банки или предполагаемые идеальные образы таких банков. По мере преуспевания банков, точки, соответствующие эталонам этих банков, распределены по другим рейтинговым областям.
Каждая точка экрана, отображающая банк-эталон, жёстко закреплена за нейроном выходного слоя, указывающего на её координаты. В результате мониторинга по принципу ассоциативного мышления, на экране должна появиться точка, соответствующая анализируемому банку. По её попаданию в область рейтинга известных банков, или по совпадению этой точки с точкой известного эталона, следует судить о значении рейтинга банка.
В системах компьютерной графики точка начала координат расположена в левом нижнем углу экрана монитора. Для её переноса в центр с учётом "сплющивания" по оси ординат необходимо выполнить преобразование:
x = x* - x0, y = k(y* - y0).
Здесь x, y – декартовы координаты точки экрана рейтинговых областей, x*, y* - декартовы координаты этой точки в используемой графической системе, x0, y0 – координаты центра экрана в этой системе, k – коэффициент "сплющивания" экрана по оси ординат.
Однако экран, связанный с декартовой системой координат, как следует из рисунка, затрудняет интерполяцию, необходимую при ассоциативном выводе. А именно, найденная на основе усреднения координата двух точек, принадлежащих некоторому, предположим, - низкому, рейтингу, может оказаться между этими точками и принадлежать области высокого рейтинга.
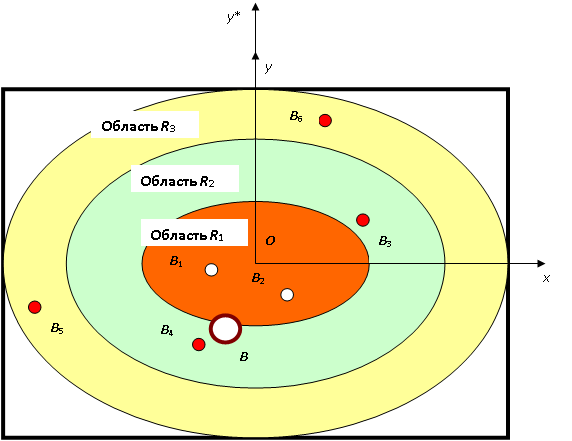
Для облегчения интерполяции целесообразно в качестве рабочей использовать сферическую систему координат 
(рис. 11.3), связанной с декартовой соотношениями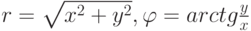 
. Центр О совпадает с центром экрана. Тогда области одинакового рейтинга оказываются ограниченными сферическими эллипсами, как показано на рисунке.
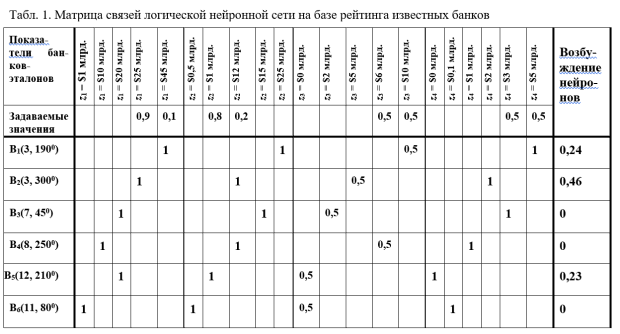
Поясним размещение на рисунке точек B1 – B6 (точка В рассмотрена далее). Пусть в декартовой системе координат известны и произвольно распределены по областям одинакового рейтинга точки, соответствующие банкам: B1(6, 6), B2(8, 5), B3(3, 7), B4(7, 3), B5(12, 6), B6(4, 1). Тогда в сферической системе координат на рис. 4.3 эти точки определяются как: B1(3, 190o), B2(3, 300o), B3(7, 45o), B4(8, 250o), B5(12, 210o), B6(11, 80o) .
Пример определения рейтинга на основе банков - эталонов
Все рекомендуемые построения проиллюстрируем простым примером, не претендующим на правильность применения в финансовой деятельности. Пусть Экспертный Совет выделил четыре показателя (фактора) для банковского мониторинга:
- z1 – собственный капитал;
- z2 – вклады населения;
- z3 – объём вложений в культурные программы ЮНЕСКО;
- z4 – объём прибыли.
Рейтинг банка может быть: R1 – высокий, R2 – средний, R3 – низкий. При этом вполне справедливо учитывать показатель z3 с весом 0,5.
Тогда каждому банку В соответствует вектор его показателей B(z1, z2, z3, z4), лежащий в основе определения его рейтинга.
Пусть известен рейтинг ряда крупных международных банков на основе их показателей:
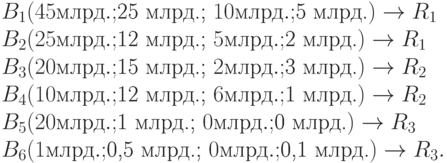
Эти соотношения определяют исходное содержание базы знаний (БЗ), которое может дополняться в ходе эксплуатации.
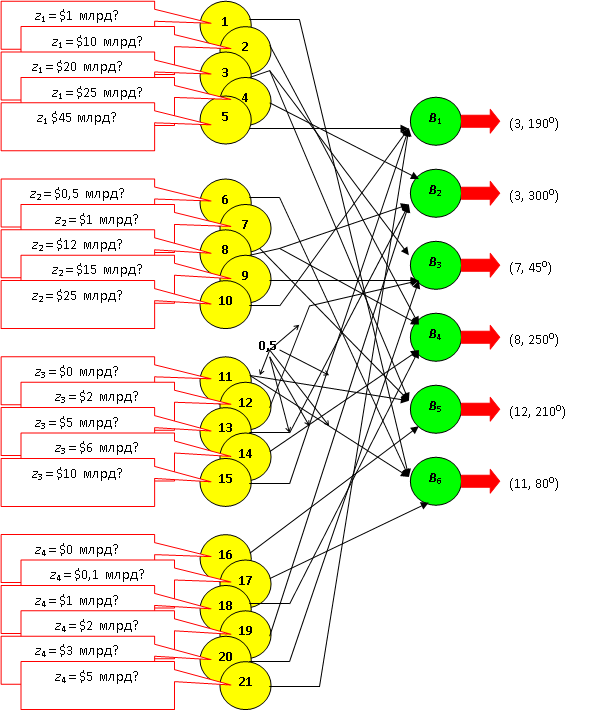
На рис. 11.4 представлена логическая нейронная сеть, соответствующая данной БД. Рецепторы 1 – 21, в соответствии со значением достоверности приведённых при них высказываний, указывают на координаты точек на экране, соответствующих банкам-эталонам. Единичные веса не обозначены.
По предполагаемым, возможно, неточным показателям методом ассоциативных вычислений находится точка, соответствующая анализируемому банку. По области её попадания делается вывод о рейтинге этого банка.
Пример 1. Найдём рейтинг банка B по предполагаемым показателям ($28 млрд.; $3 млрд.; $8 млрд.; $4 млрд.)
Приведём общий приём возбуждения рецепторов. А именно для возбуждения рецепторов, закреплённых за каждым показателем, делим "единицу" обратно пропорционально расстоянию значения испытываемого показателя между двумя ближайшими значениями этого показателя, отображёнными в сети. Тогда возбуждение V4 рецептора 4 приближённо полагаем равным 0,9, а возбуждение V5 рецептора 5 – 0,1. Аналогично, приблизительно полагаем V7 = 0,8, V8 = 0,2, V14 = V15 = V20 = V21 = 0,5. Возбуждение остальных рецепторов равно нулю.
По функции активации при h = 0,2 (значение порога подбирается так, чтобы исключить из рассмотрения малые возбуждения) находим возбуждение нейронов, соответствующих точкам банков – эталонов на экране: VB1 = 0,24, VB2 = 0,46, VB3 = VB4 = 0, VB5 = 0,23, VB6 = 0. Используя полученные значения возбуждения нейронов в качестве весов, по известной формуле нахождения среднего найдём значение координат искомой точки B на экране:
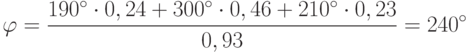
На рис. 11.3 показано примерное положение найденной точки B на экране. Она принадлежит области среднего рейтинга R2.
Построение обученной логической нейронной сети на основе интервалов значений показателей
Обучение рейтинговой системы с помощью известных рейтингов банков, принимаемых за эталон, приводит, как показано выше, к достаточно громоздким логическим нейронным сетям. Ведь они должны развиваться с обретением новых знаний. Следует учесть, однако, высокую степень наглядности и "дружественный" интерфейс. Несомненно, более точно и оперативно используется накопленный опыт.
Можно создавать значительно более простые логические нейронные сети, если известны диапазоны принадлежности значений показателей, в совокупности определяющие то или иное значение рейтинга.
Например, пусть на основе изучения рейтинга приведённых выше банков и значительного количества других, оказалось целесообразным выделить по два значимых диапазона возможной принадлежности каждого показателя банка. Пусть z1 определяется отрезками (возможно, полуоткрытыми) значений [0, 25) и [25, 50], z2 – отрезками [0, 10) и [10, 25], z3 – отрезками [0, 5) и [5, 10], z4 - отрезками [0, 2) и [2, 5].
На основе информации экспертов составляется логическое описание системы принятия решений. В соответствии с результатами исследований, отображённых в приведённой литературе, оно должно состоять из исчерпывающего, непротиворечивого набора логических функций – импликаций. Каждая логическая функция в левой части представляет собой конъюнкцию, в общем случае, дизъюнкций высказываний о принадлежности данных. То есть, в левой части отображается ситуация. В правой части, после знака следования, указывается значение рейтинга. Таким образом, правые части отображают приём "размножения решений", способствующий непротиворечивости и возможности модификации.
При этом для сокращения объёма сети, в левых частях логических функций можно использовать объединение данных одного фактора (показателя) в дизъюнкции так, чтобы при раскрытии скобок не сформировались ситуации, для которых предусмотрено решение, отличное от указанного в правой части. Это означает, что при неправильном формировании логического описания одни ситуации могут поглотить другие, требующие отличающегося решения.
В то же время, попытки сократить объём логической нейронной сети за счёт объединения ситуаций, требующих одного и того же решения, с помощью операции дизъюнкции, вполне справедливы.
Пусть логическое описание, удовлетворяющее указанным требованиям полноты и непротиворечивости, имеет вид:
![(z_1\in [25, 50])\land (z_2\in [10, 25])\land ((z_3\in [0, 5))\lor ( z_3\in [5, 10]))\land (z_4\in [2, 5]) \to Q_1 = <Рейтинг банка высокий>; \\
(z_1\in [0, 25))\land (z_2\in [10, 25])\land (z_3\in [5, 10])\land (z_4\in [2, 5]) \to Q_2 = <Рейтинг банка средний>;\\
(z_1\in [25, 50])\land (z_2\in [10, 25])\land ((z_3\in [0, 5))\lor ( z_3\in [5, 10]))\land (z_4\in [0, 2)) \to Q_3 = <Рейтинг банка средний>;\\
(z_1\in [25, 50])\land (z_2\in [10, 25])\land (z_3\in [0, 5))\land (z_4\in [2, 5]) \to Q_4 = <Рейтинг банка средний>\\
(z_1\in [0, 25))\land (z_2\in [0, 10))\land ((z_3\in [0, 5))\lor ( z_3\in [5, 10]))\land (z_4\in [0, 2)) \to Q_5 = <Рейтинг банка низкий>;](/sites/default/files/tex_cache/22d9e87456defedf49cbc743c3086d6c.png)
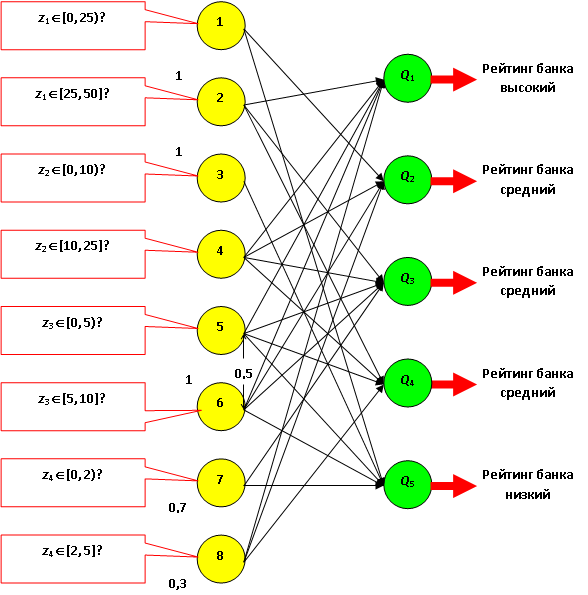
Обученная логическая нейронная сеть, напрямую связывающая диапазоны показателей с рейтингом банка и учитывающая веса связей (0,5 - вес всех связей, исходящих из вершин 5 и 6), показана на рис. 11.5. Рецепторы 1 – 8 возбуждаются в соответствии с достоверностью указанных при них высказываний. Легко видеть, что рассмотренные ранее банки – эталоны точно отражены в этой сети.
Однако использованная ранее функция активации здесь не подходит, т.к. на некоторых нейронах объединяется не единственная конъюнкция событий, а дизъюнкция таких конъюнкций. Целесообразно выбрать следующую функцию активации:
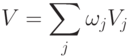
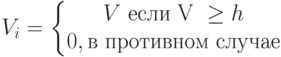
Здесь, как и прежде, Vi – искомая величина возбуждения i-го нейрона, Vj – величина возбуждения j-го нейрона (рецептора), связанного с i-м, 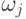– вес этой связи.
Если предполагается данную сеть использовать в длинной логической цепочке, где значения возбуждения нейронов тотчас поступают на рецепторы другой логической нейронной сети, то необходимо выполнить нормирование формируемых возбуждений. Тогда значение V следует разделить на максимально возможное значение возбуждения нейрона. В данном примере это значение равно 3,5.
Пример 2. Определим рейтинг банка B, рассмотренного в примере 1, с учётом того, что показатель z4 (объём прибыли) определён неточно и составляет не то $1,5 млрд., не то $4 млрд. Размышляя трезво, аналитик предположил, что первая оценка верна на 70%, а вторая, соответственно, на 30%. Зададим возбуждение рецепторов: V2 = 1, V3 = 1, V6 = 1, V7 = 0,7, V8 = 0,3. (Значения отмечены на рисунке.) C помощью функции активации, положив h = 1, находим VQ1 = 1,8, VQ2 = 0, VQ3 = 2,2, VQ4 = 1,3, VQ5 = 2. Так как максимального возбуждения достигает нейрон Q3, банк В обладает средним рейтингом.
Возникает лишь вопрос об отображении полученной сети на экране монитора.
Отображение и управление рейтинговой системой с помощью матриц связей
Существует универсальный способ представления и обработки логических нейронных сетей с помощью матриц связей, отображённых на экране монитора.
Однако матрицу связей логической нейронной сети, связывающей диапазоны значений показателей с рейтингом банка (табл. 11.2), не следует считать менее информативным и оперативным средством управления, модификации и развития рейтинговой системы.
| Интервалы показателей банков | z1\in [0, 25) | z1\in [25, 50] | z2\in [0, 10) | z2\in [10, 25] | z3\in [0, 5) | z3\in [5, 10] | z4\in [0, 2) | z4\in [2, 5]? | Возбуждение нейронов |
|---|---|---|---|---|---|---|---|---|---|
| Задаваемые оценки принадлежности | 1 | 1 | 1 | 0,7 | 0,3 | ||||
| R1 = <Рейтинг высокий> | 1 | 1 | 0,5 | 0,5 | 1 | 1,8 | |||
| R2 = <Рейтинг средний> | 1 | 1 | 0,5 | 1 | 0 | ||||
| R3 = <Рейтинг средний> | 1 | 1 | 0,5 | 0,6 | 1 | 2,2 | |||
| R4 = <Рейтинг средний> | 1 | 1 | 0,5 | 1 | 1,3 | ||||
| R5 = <Рейтинг низкий> | 1 | 1 | 0,5 | 0,5 | 1 | 2 |
Краткие итоги
- Логическая нейронная сеть позволяет легко вводить в рассмотрение и исключать из рассмотрения любые количества факторов, влияющих на рейтинг банка.
- Главным достоинством рассматриваемой системы является её работа по нечётким данным.
- Обучение рейтинговой системы банковского мониторинга основано на экспертных оценках ряда известных банков по их классификации. Динамический учёт дрейфа рейтинга банков-эталонов производится оперативно, путём несложных операций перевода их в другую рейтинговую область экрана.
- Рассмотренная здесь система выполняет "голосование", с получением веса, в пользу одного или более близких по рейтингу банков-эталонов, допуская усреднение с помощью этих весов.
- Унифицированный программный продукт на основе рассмотренных логических нейронных сетей должен быть инвариантным относительно количества рецепторов и количества нейронов выходного слоя. Изменение этих параметров и связей пользователем-оператором должно производиться с помощью матриц следования.
- Применение логических нейронных сетей в рейтинговых системах весьма результативно в системах приоритетного планирования, управления качеством, оценки результатов трудовой деятельности, в социальных системах, в образовании – во всех системах и приложениях, где точная математическая интерпретация процессов невозможна или весьма трудоёмка.
Вопросы
- Как на экране следует представлять исходные данные для мониторинга?
- Как целесообразно отображать результаты мониторинга?
- В чём преимущества представления результатов мониторинга в сферической системе координат по сравнению с декартовой?