Разработка сетевого графика проекта
Процесс расчета параметров сетевого графика
Сетевой график проекта располагает операции в подходящей последовательности для расчета времени начала и окончания операции. Оценка продолжительности операции проводится на основе затрат времени, требуемого для решения всех задач, составляющих набор работ операции.
С помощью нескольких простых расчетов можно выполнить прямой и обратный анализ сетевого графика проекта. Этот анализ даст ответы на следующие вопросы:
Прямой анализ - Определение ранних сроков начала операций
- Как скоро может начаться операция? (ранний старт - ES )
- Как скоро она может закончиться? (ранний финиш- EF )
- Как скоро может быть завершен проект в целом? (предполагаемое время- ТЕ )
Обратный анализ - Определение поздних сроков завершения операций
- Каковы самые поздние сроки начала операции? (позднее начало - LS )
- Каковы самые поздние сроки завершения операции? (позднее окончание - LF )
- Какие операции составляют критический путь ( СР )? Это самый длинный путь, при задержке выполнения операций на этом пути задерживается выполнение проекта.
- На какое время может быть задержано выполнение операции? (резерв времени - SL )
Термины в скобках являются общепринятыми обозначениями и используются в большинстве книг по управлению проектами
Прямой анализ - определение ранних сроков начала операций
Процесс прямого анализа разворачивается от первых операций проекта, проходя по всем цепочкам последовательных операций сетевого графика до самой последней операции проекта.
По мере продвижения по любому из путей производится добавление времени выполнения операций. Самый длинный путь показывает время завершения проекта в целом и называется критическим путем ( СР ).
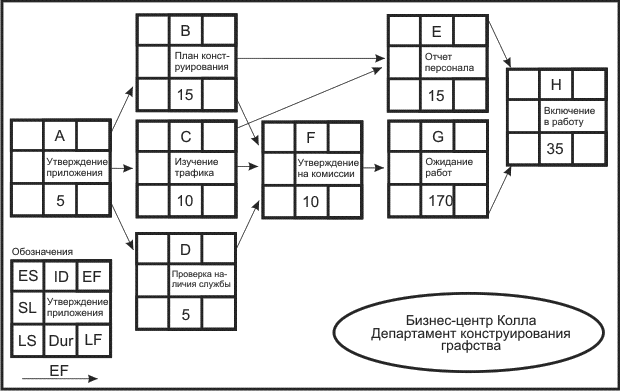
В табл. 2.2 представлено время операций в рабочих днях для проекта бизнес-центра Колла.
На рис. 2.5 показана система с оценкой продолжительности операций, которую вы можете видеть в блоке.
Например, операция А имеет продолжительность 5 дней, операция G -170 рабочих дней.
Поступательный путь начинается со времени начала проекта, которое обычно принимается равным нулю.
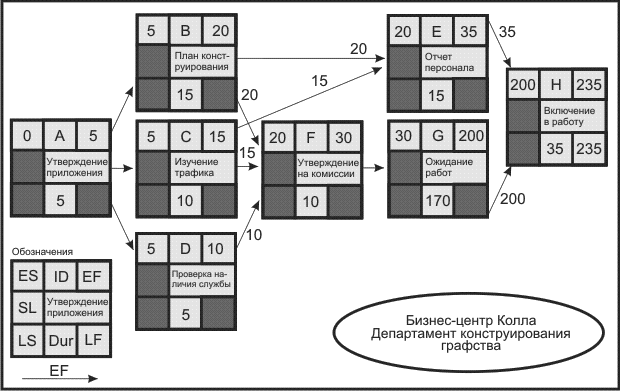
В нашем примере, ранний срок начала первой операции (операция- А ) это 0. Это время проставляется в верхнем левом углу блока операции А (рис. 2.6).
Самое раннее окончание операции А это 5 ( ES + Dur или 0 + 5 = 5 ).
Далее мы видим, что операция А предшествует операциям B, C, D.
Следовательно, самое раннее время начала этих операций - это момент завершения операции А, 5 рабочих дней.
На рис. 2.6 можно видеть, что операции В, С и D могут начаться в момент завершения операции А, и поэтому все они имеют раннее начало ( ES ) 5.
Используя формулу ES + Dur = EF, раннее время завершения этих операций - В, C, D -( EF ) будет, соответственно, 20, 15, и 10.
Какое же тогда будет раннее время начала ( ES ) для операции Е, которая является операцией слияния?
Это будет 15 или 20? Ответ - 20, так как все операции, непосредственно предшествующие операции Е ( В и С ) должны быть завершены до начала операции Е. Поскольку для завершения операции В требуется более продолжительное время, она и определяет раннее начало ( ES ) операции Е.
Тот же процесс используется для определения ES для операции F. Ей предшествуют операции В, C, и D. Операция В является определяющей для времени раннего окончания ( EF ), которой требуется больше времени ( 20 против 15 и 10 ), чем операциям ( В, C, и D ), непосредственно предшествующим операции F.
Прямой анализ предполагает, что каждая операция начинается в тот момент, когда завершается последняя предшествующая ей операция. При расчете времени раннего начала операций в процессе прямого анализа необходимо помнить три вещи:
- Вы добавляете время операции на каждом шаге анализа ( ES + Dur = EF )
- Вы переносите раннее завершение ( EF ) предшествующей операции до следующей, у которой оно же становится временем раннего начала ( ES ), если только
- Последующая операция не является операцией слияния.В этом случае вы выбираете самое большое по значению время раннего окончания ( ЕF ) среди всех непосредственно предшествующих операций.
В нашем примере на рис. 2.6 ЕF для операции F (30) проводится до операции G, где становится ее ES (30).
Мы видим, что операция Н является операцией слияния и, следовательно, необходимо найти самое большое по значению EF у непосредственно предшествующих ей операций ( Е и G ). В этом случае выбор происходит между временем EF 35 и 200 ; выбор ES операции Н 200 EF для операции Н ( 235 ) становится самым ранним расчетным временем ( ТЕ ), когда проект может быть завершен в целом.
Таким образом, на все три вопроса, которые ставятся в процессе прямого анализа, были получены ответы.
Обратный анализ - определение поздних сроков завершения операций
Обратный анализ начинается с самой последней операции сетевого графика.
Каждый раз, выполняя шаг назад к началу сетевого графика, необходимо вычитать время рассматриваемой операции из общей продолжительности проекта в целом, с тем, чтобы определить сроки ее самого позднего возможного начала ( LS ) и окончания ( LF ) выполнения. За исходную временную точку при выполнении обратного анализа выбирается время позднего окончания самой последней операции проекта. В этой операции данное время совпадает с временем раннего окончания ее выполнения ( EF ) (или в случае нескольких завершающих операций, операции с самым большим ( EF )). В некоторых случаях имеются установленные крайние сроки продолжительности проекта, тогда будут использоваться именно эти сроки. Предположим, что мы можем принять EF предполагаемого окончания проекта ( ТЕ ) равным 235 рабочим дням. LF для операции Н становится 235 рабочих дней ( EF ~ LF ) (см. рис. 2.7).
Обратный анализ похож на прямой. Выполняя его, следует помнить три вещи:
- Вы вычитаете время операции на каждом шаге, начиная с последней операции проекта ( LF - Dur = LS ).
- Вы переносите LS на предшествующую операцию и приравниваете ей LF к ней, если
- Предшествующая операция не является операцией дробления; в противном случае вы выбираете наименьший LS из всех операций, которым данная операция дает начало, и приравниваете к этому значению ее LF.
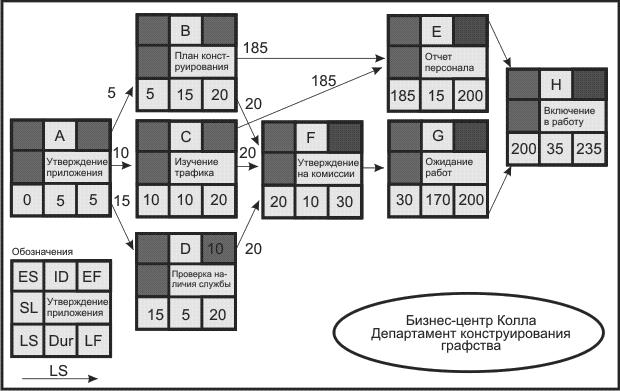
Давайте применим эти правила к нашему примеру с бизнес-центром Колла. Начинаем с операции Н (включение в работу) и ее LF в 235 рабочих дней, LS для операции Н оказывается равным 200 рабочих дней ( LF - Dur = LS или 235 - 35 = 200 ).
LS для операции Н становится LF для операций Е и G. LS для операций Е и G становится соответственно 185 ( 200 - 15 = 185 ) и 30 рабочих дней ( 200 - 170 = 30 ).
LS для операции G становится LF для операции F, и ее LS становится 20.
Здесь мы видим, что операции В и C являются операциями дробления, которые связаны с операциями Е и F. Поздний финиш для операции В контролируется LS операций Е и F. LS для операции Е - 185 дней и для операции F - 20 дней. Идите по стрелке назад от операций Е и F к операции В.
Отметим, что время LS для операций Е и F помещено в правый блок, и вы можете выбрать наименьшее время - 20 дней.
Заключительная операция В может быть завершена за 20 дней; в противном случае выполнение операции F задержится, задержится и выполнение проекта.
LF для операции C идентично операции В, поскольку она также определяет LS операций Е и F.
Операция D просто получает свое позднее окончание ( LF ) от операции F.
Вычислив LS ( LF - Dur = LS ) для операций В, C, D, мы можем определить LF для операции А, которая является операцией дробления.
Окончание операции А определяется операцией В, которая является наименьшим LS для операций В, С и D.
Так как LS для операции В составляет период времени 5, LF для операции А - 5, и ее LS - период времени - 0.
Обратный анализ завершен, и сроки последней операции известны.