| №№ пп. |
Термины |
Определения |
Примечания |
|
|
1. Теория вероятностей |
|
|
|
1.1. Общие понятия |
|
| 1.1.1. |
Пространство элементарных событий
|
Множество, элементы которого, называемые элементарными событиями, соответствуют возможным результатам наблюдения, измерения, анализа, проверки, исходам опыта, эксперимента, испытания. |
Пространство элементарных событий 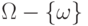 лежит в основе вероятностных моделей явлений (процессов). Вместо явного описания пространства элементарных событий часто используют косвенное или частичное описание, например, с помощью распределений случайных величин лежит в основе вероятностных моделей явлений (процессов). Вместо явного описания пространства элементарных событий часто используют косвенное или частичное описание, например, с помощью распределений случайных величин |
| 1.1.2 |
Случайное событие |
Измеримое подмножество пространства элементарных событий
|
Термин "измеримое" понимают в смысле теории измеримых множеств. Случайные события образуют  -алгебру -алгебру 
|
| 1.1.3 |
Вероятностная мера |
Сигма-аддитивная мера  , определенная на всех случайных событиях и такая, что , определенная на всех случайных событиях и такая, что 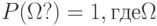 ? - пространство элементарных событий ? - пространство элементарных событий
|
Вероятностная мера  - функция, ставящая в соответствие каждому случайному событию - функция, ставящая в соответствие каждому случайному событию  его вероятность его вероятность 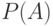 . Термин "мера" понимают в смысле математической теории меры. Синонимы: вероятностное распределение, распределение вероятностей, распределение, вероятность на пространстве элементарных событий. . Термин "мера" понимают в смысле математической теории меры. Синонимы: вероятностное распределение, распределение вероятностей, распределение, вероятность на пространстве элементарных событий. |
| 1.1.4. |
Вероятностное пространство |
Совокупность 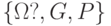 пространства элементарных событий пространства элементарных событий  ?, класса случайных событий ?, класса случайных событий  и вероятностной меры и вероятностной меры  . . |
Вероятностное пространство (синоним: поле вероятностей) - основной исходный объект теории вероятностей и вероятностных моделей реальных явлений (процессов). |
| 1.1.5. |
Вероятность события 
|
Значение 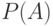 вероятностной меры вероятностной меры  на случайном событии на случайном событии 
|
В силу закона больших чисел частота реализации события  при неограниченном увеличении числа независимых повторений одного и того же комплекса условий, описываемого вероятностным пространством при неограниченном увеличении числа независимых повторений одного и того же комплекса условий, описываемого вероятностным пространством 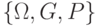 , стремится к вероятности этого события , стремится к вероятности этого события 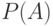 , т.е. для любого , т.е. для любого 
 , ,где 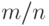 - частота, - частота,  - вероятность события - вероятность события  , ,  - число повторений. Это свойство нельзя принимать за определение вероятности события в математической теории вероятностей. Оно указывает способ оценивания вероятности по опытным данным. - число повторений. Это свойство нельзя принимать за определение вероятности события в математической теории вероятностей. Оно указывает способ оценивания вероятности по опытным данным.
|
| 1.1.6. |
Независимость случайных событий |
Случайные события  и и  являются независимыми, если являются независимыми, если 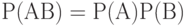 , где , где 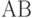 - пересечение множеств - пересечение множеств  и и  (произведение событий (произведение событий  и и  ). Случайные события ). Случайные события 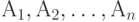 называются независимыми (в совокупности), если называются независимыми (в совокупности), если  и аналогичные равенства справедливы для всех поднаборов этих событий и аналогичные равенства справедливы для всех поднаборов этих событий 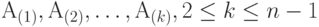
|
Общематематическое понятие пересечения множеств 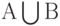 в теории вероятностей по традиции эквивалентно понятию произведения событий в теории вероятностей по традиции эквивалентно понятию произведения событий 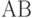 . . |
| 1.1.7 |
Случайный элемент |
Измеримая функция, определенная на вероятностном пространстве |
Случайный элемент  принимает значения в измеримом пространстве принимает значения в измеримом пространстве 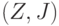 , где , где  - пространство значений - пространство значений  , а , а 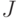 - класс измеримых подмножеств - класс измеримых подмножеств  ; при этом для любого ; при этом для любого  множество множество 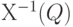 является случайным событием. является случайным событием.
Если  - множество действительных чисел - множество действительных чисел 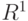 , то случайный элемент , то случайный элемент  называют случайной величиной. Если называют случайной величиной. Если 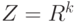 - конечномерное векторное пространство размерности - конечномерное векторное пространство размерности 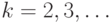 , то случайный элемент , то случайный элемент  называют случайным вектором. называют случайным вектором.
|
| 1.1.8. |
Распределение случайного элемента |
Функция множества, задающая вероятность принадлежности случайного элемента измеримому подмножеству его области значений |
Для случайного элемента  , определенного на вероятностном пространстве , определенного на вероятностном пространстве 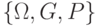 со значениями в измеримом пространстве со значениями в измеримом пространстве 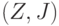 , его распределение , его распределение ![P_1:J -\to [0,1]](/sites/default/files/tex_cache/bfc756bbd0cbecf84df5712578077d16.png) задается формулой задается формулой 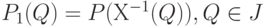 . . |
| 1.1.9. |
Дискретный случайный элемент |
Случайный элемент, область значений которого состоит из конечного или счетного множества точек. |
Распределение случайного элемента  , принимающего только значения , принимающего только значения 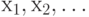 , полностью описывается числами , полностью описывается числами  , причем , причем 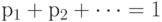 . . |
| 1.1.10 |
Параметрическое семейство распределений |
Функция, определенная на параметрическом пространстве (подмножестве конечномерного векторного пространства), которая каждому значению параметра (числу или вектору, входящему в параметрическое пространство) ставит в соответствие распределение случайного элемента. |
Параметр может быть одномерным или конечномерным. Вместо "зависимость от  -мерного параметра" часто говорят "зависимость от k параметров". -мерного параметра" часто говорят "зависимость от k параметров". |
| 1.1.11 |
Независимость случайных элементов |
Определенные на одном и том же вероятностном пространстве случайные элементы 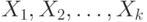 со значениями в измеримых пространствах со значениями в измеримых пространствах 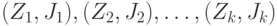 соответственно называются независимыми, если для любых соответственно называются независимыми, если для любых 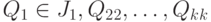 имеем имеем  . . |
Для случайных величин и векторов, имеющих плотности вероятности, независимость эквивалентна тому, что плотность вероятности вектора 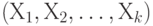 равна произведению плотностей вероятностей случайных величин равна произведению плотностей вероятностей случайных величин 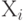 , т.е. , т.е.  . Результаты экспериментов, которые проведены независимо друг от друга, как правило, моделируются с помощью независимых случайных величин. . Результаты экспериментов, которые проведены независимо друг от друга, как правило, моделируются с помощью независимых случайных величин. |
| 1.1.12 |
Вероятностная модель явления (процесса) |
Математическая модель явления (процесса), в которой использованы понятия теории вероятностей и математической статистики |
Установление (формулировка) исходной вероятностной модели - необходимый первый этап для применения методов прикладной статистики |
|
|
1.2. Случайная величина |
|
| 1.2.1. |
Случайная величина |
Однозначная действительная измеримая функция на вероятностном пространстве |
Однозначная действительная функция 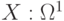 является случайной величиной, если для любого является случайной величиной, если для любого 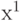 множество множество  является случайным событием. Случайная величина - это случайный элемент со значениями в является случайным событием. Случайная величина - это случайный элемент со значениями в 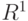 . (Здесь . (Здесь 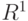 - множество действительных чисел.) - множество действительных чисел.) |
| 1.2.2. |
Функция распределения |
Функция, определяющая для всех действительных чисел  вероятность того, что случайная величина вероятность того, что случайная величина  принимает значения, меньшие принимает значения, меньшие 
|
Функция распределения 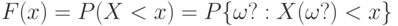 . Функция распределения непрерывна слева. Примечание. Иногда функцию распределения определяют как . Функция распределения непрерывна слева. Примечание. Иногда функцию распределения определяют как 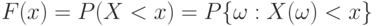 . Тогда она непрерывна справа . Тогда она непрерывна справа |
| 1.2.3. |
Плотность вероятности |
Функция 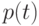 такая, что такая, что  , при всех , при всех  , где , где  - функция распределения рассматриваемой случайной величины - функция распределения рассматриваемой случайной величины |
Сокращенная форма: плотность |
| 1.2.4. |
Непрерывная случайная величина |
Случайная величина, функция распределения которой при всех действительных  непрерывна непрерывна |
|
| 1.2.5 |
Квантиль порядка 
|
Значение случайной величины, для которого функция распределения принимает значение  или имеет место "скачок" со значения меньше или имеет место "скачок" со значения меньше  до значения больше до значения больше 
|
Число 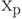 - квантиль порядка р для случайной величины с функцией распределения - квантиль порядка р для случайной величины с функцией распределения  тогда и только тогда, когда тогда и только тогда, когда 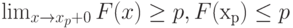 . Может случиться, что вышеуказанное условие выполняется для всех значений . Может случиться, что вышеуказанное условие выполняется для всех значений  , принадлежащих некоторому интервалу. Тогда каждое такое значение называется квантилью порядка , принадлежащих некоторому интервалу. Тогда каждое такое значение называется квантилью порядка  .
Примечание. Одни авторы употребляют термин "квантиль" в мужском роде, другие - в женском. .
Примечание. Одни авторы употребляют термин "квантиль" в мужском роде, другие - в женском. |
| 1.2.6. |
Медиана |
Квантиль порядка 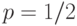 . . |
|
| 1.2.7. |
Мода непрерывной случайной величины |
Значение случайной величины, соответствующее локальному максимуму ее плотности вероятности |
Мод у непрерывной случайной величины может быть несколько (конечное число или бесконечно много). Краткая форма термина: мода |
| 1.2.8. |
Математическое ожидание |
Среднее взвешенное по вероятностям значение случайной величины  , т.е. , т.е. 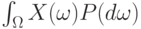
|
Математическое ожидание обозначают 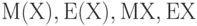 и др. Рекомендуемое обозначение: и др. Рекомендуемое обозначение: 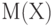 . При этом . При этом 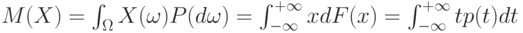 , где , где  - функция распределения, а - функция распределения, а 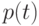 - плотность вероятности случайной величины - плотность вероятности случайной величины 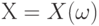 . Математическое ожидание существует не для всех случайных величин . Математическое ожидание существует не для всех случайных величин  . Для существования математического ожидания необходимо и достаточно абсолютной сходимости соответствующего интеграла . Для существования математического ожидания необходимо и достаточно абсолютной сходимости соответствующего интеграла |
| 1.2.9. |
Дисперсия (случайной величины  ) ) |
Математическое ожидание квадрата разности между случайной величиной и ее математическим ожиданием |
Для случайной величины  дисперсия дисперсия 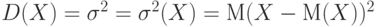 . Дисперсия равна 0 тогда и только тогда когда . Дисперсия равна 0 тогда и только тогда когда 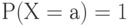 для некоторого а для некоторого а |
| 1.2.10 |
Среднее квадратическое отклонение |
Неотрицательный квадратный корень из дисперсии |
|
| 1.2.11 |
Коэффициент вариации
|
Отношение среднего квадратического отклонения к математическому ожиданию |
Применяется для положительных случайных величин как показатель разброса |
| 1.2.12. |
Момент порядка  (случайной величины (случайной величины  ) ) |
Математическое ожидание случайной величины 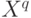
|
|
| 1.2.13 |
Центральный момент порядка q (случайной величины  ) ) |
Математическое ожидание случайной величины 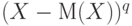 , где М(Х) - математическое ожидание , где М(Х) - математическое ожидание  . . |
Дисперсия - центральный момент порядка 2. |
| 1.2.14 |
Характеристи-ческая функция (случайной величины  ) ) |
Функция от  при каждом при каждом  равная математическому ожиданию случайной величины равная математическому ожиданию случайной величины  , где , где  - мнимая единица, - мнимая единица,  - основание натуральных логарифмов - основание натуральных логарифмов |
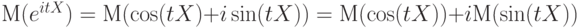 . . |
|
|
1.3. Случайный вектор |
|
| 1.3.1. |
Случайный вектор |
Однозначная измеримая функция на вероятностном пространстве со значениями в конечномерном евклидовом пространстве 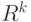 . . |
Случайный вектор  - это случайный элемент со значениями в - это случайный элемент со значениями в 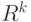 , т.е. , т.е. 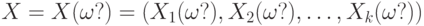 , где , где 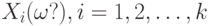 , - случайные величины, заданные на одном и том же вероятностном пространстве , - случайные величины, заданные на одном и том же вероятностном пространстве |
| 1.3.2. |
Функция распределения (случайного вектора) |
Функция распределения 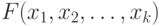 случайного вектора случайного вектора  удовлетворяет равенству удовлетворяет равенству  . . |
|
| 1.3.3. |
Плотность вероятности (случайного вектора) |
Функция 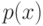 такая, что такая, что  для случайного вектора для случайного вектора 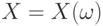 и любого борелевского подмножества и любого борелевского подмножества  конечномерного евклидова пространства конечномерного евклидова пространства 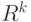 . . |
|
| 1.3.4. |
Математическое ожидание случайного вектора |
Вектор, компоненты которого - математические ожидания компонент случайного вектора |
Математическое ожидание случайного вектора 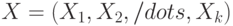 есть есть 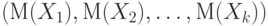 , где , где 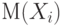 - математическое ожидание случайной величины - математическое ожидание случайной величины  , являющейся , являющейся  - ой компонентой случайного вектора - ой компонентой случайного вектора  , , 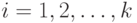 . . |
| 1.3.5. |
Ковариация (для двумерного вектора) |
Ковариацией вектора  называется математическое ожидание случайной величины называется математическое ожидание случайной величины 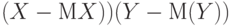 , где , где  и и 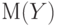 - математические ожидания случайных величин - математические ожидания случайных величин  и и  . . |
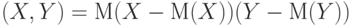 ; если ; если 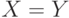 , то , то 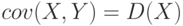 - дисперсия - дисперсия  . . |
| 1.3.6. |
Ковариационная матрица случайного вектора |
Квадратная матрица 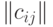 порядка порядка  , в которой , в которой 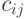 - ковариация двумерного вектора - ковариация двумерного вектора 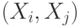 , где , где  и и  - компоненты случайного вектора - компоненты случайного вектора 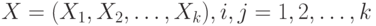 . . |
Ковариационная матрица симметрична, на главной диагонали стоят дисперсии  - компонент - компонент 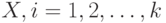 . . |
| 1.3.7. |
Коэффициент корреляции (для двумерного вектора) |
Отношение ковариации вектора  к произведению средних квадратических отклонений к произведению средних квадратических отклонений 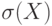 и и 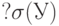 случайных величин случайных величин  и и 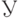 . . |
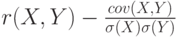 . Если . Если  . Верно и обратное: если . Верно и обратное: если 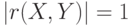 , то , то 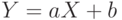 .. .. |
| 1.3.8. |
Корреляционная матрица случайного вектора |
Квадратная матрица 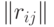 порядка порядка  , в которой , в которой 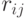 - коэффициент корреляции двумерного вектора - коэффициент корреляции двумерного вектора 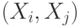 , где , где  и и  - компоненты случайного вектора - компоненты случайного вектора 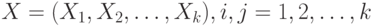 . . |
Корреляционная матрица симметрична, на главной диагонали стоят единицы |
|
|
2. Прикладная статистика |
|
|
|
2.1. Общие понятия |
|
| 2.1.1. |
Признак |
Свойство (характеристика) объекта наблюдения |
Частными видами наблюдения являются измерение, испытание, анализ, опыт, проверка и т.д. |
| 2.1.2. |
Результат наблюдения |
Значение признака объекта наблюдения |
Результат наблюдения может быть числом, вектором, элементом конечного множества или математическим объектом иной природы |
| 2.1.3. |
Выборка |
Совокупность значений одного и того же признака у подвергнутых наблюдению объектов |
Выборка - совокупность чисел или векторов, или математических объектов иной природы, соответствующих изучаемым реальным объектам наблюдения |
| 2.1.4. |
Объем выборки
|
Число результатов наблюдений, включенных в выборку |
Объем выборки обычно обозначают  . . |
| 2.1.5. |
Вероятностная модель выборки |
Вероятностная модель получения результатов наблюдений, включаемых в выборку |
Примерами вероятностных моделей выборок являются простая случайная выборка и случайная выборка из конечной совокупности |
| 2.1.6. |
Простая случайная выборка
|
Выборка, в которой результаты наблюдений моделируются как совокупность независимых одинаково распределенных случайных элементов |
Если результаты наблюдений имеют распределение F, то говорят, что "выборка извлечена из распределения F". |
| 2.1.7. |
Случайная выборка из конечной совокупности |
Выборка объема  , в которую включены результаты наблюдений над объектами, отбираемыми из конечной совокупности так, что любой набор n объектов имеет одинаковую вероятность быть отобранным , в которую включены результаты наблюдений над объектами, отбираемыми из конечной совокупности так, что любой набор n объектов имеет одинаковую вероятность быть отобранным |
Если  - число объектов конечной совокупности, то для получения случайной выборки объема - число объектов конечной совокупности, то для получения случайной выборки объема  из этой совокупности, из этой совокупности,  , отбор объектов для проведения наблюдений должен проводиться так, чтобы любой набор из , отбор объектов для проведения наблюдений должен проводиться так, чтобы любой набор из  объектов имел одну и ту же вероятность быть отобранным, равную объектов имел одну и ту же вероятность быть отобранным, равную  !, т.е. обратной величине к числу сочетаний из !, т.е. обратной величине к числу сочетаний из  элементов по элементов по  . . |
| 2.1.8. |
Статистика |
Измеримая функция результатов наблюдений, включенных в выборку, используемая для получения статистических выводов |
Статистики используются для описания данных, оценивания, проверки гипотез. Статистика, как функция случайного элемента, является случайным элементом. Статистика принимает значения в некотором измеримом пространстве 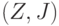 , своем для каждой статистики , своем для каждой статистики |
|
|
2.2. Описание данных |
|
| 2.2.1. |
Частота события
|
Отношение числа наблюдений, в которых осуществилось событие, к объему выборки
|
|
| 2.2.2. |
Эмпирическое распределение |
Распределение случайного элемента, в котором каждому результату наблюдения, включенному в выборку, соответствует одна и та же вероятность, равная обратной величине объема выборки |
Если в выборку включены результаты наблюдений 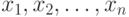 , то эмпирическое распределение - это распределение случайной величины , то эмпирическое распределение - это распределение случайной величины  такой, что такой, что 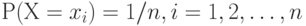 . Если несколько результатов наблюдений совпадают: . Если несколько результатов наблюдений совпадают:  , то полагают , то полагают  . . |
| 2.2.3. |
Эмпирическая функция распределения |
Функция эмпирического распределения |
Определена, когда результаты наблюдений - числа или вектора (функции распределения по пп.1.2.2 и 1.3.2 соответственно). |
| 2.2.4. |
Выборочное среднее арифметическое |
Сумма результатов наблюдений, включенных в выборку, деленная на ее объем |
Выборочное среднее арифметическое равно математическому ожиданию случайной величины, имеющей эмпирическое распределение |
| 2.2.5 |
Выборочная дисперсия |
Сумма квадратов отклонений результатов наблюдений, включенных в выборку, от их выборочного среднего арифметического, деленная на объем выборки
|
Выборочная дисперсия 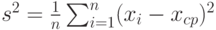 , где , где 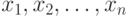 - результаты наблюдений, включенные в выборку; - результаты наблюдений, включенные в выборку; 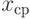 - выборочное среднее арифметическое, - выборочное среднее арифметическое, 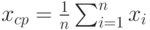 . Выборочная дисперсия равна дисперсии случайной величины, имеющей эмпирическое распределение . Выборочная дисперсия равна дисперсии случайной величины, имеющей эмпирическое распределение |
| 2.2.6. |
Выборочное среднее квадратическое отклонение |
Неотрицательный квадратный корень из выборочной дисперсии |
|
| 2.2.7. |
Выборочный момент порядка 
|
Момент порядка  случайной величины, имеющей эмпирическое распределение случайной величины, имеющей эмпирическое распределение |
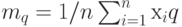 , где , где 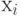 по п.2.2.5. по п.2.2.5. |
| 2.2.8. |
Выборочный центральный момент порядка 
|
Центральный момент порядка  случайной величины, имеющей эмпирическое распределение случайной величины, имеющей эмпирическое распределение |
 где где 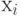 и и 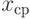 по п.2.2.5. по п.2.2.5. |
| 2.2.9 |
 -я порядковая статистика -я порядковая статистика |
 -й элемент -й элемент 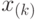 в вариационном ряду, полученном из выборки объема в вариационном ряду, полученном из выборки объема  , элементы которой , элементы которой 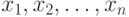 расположены в порядке неубывания: расположены в порядке неубывания:  . . |
|
| 2.2.10 |
Размах выборки |
Разность между наибольшим и наименьшим значениями результатов наблюдений в выборке |
Если 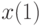 и и 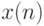 - первая и - первая и  -ая порядковые статистики в выборке объема -ая порядковые статистики в выборке объема  , то размах , то размах 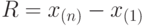 . . |
| 2.2.11. |
Выборочная ковариация |
Ковариация двумерного случайного вектора, имеющего эмпирическое распределение |
Если 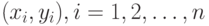 , - результаты наблюдений, включенные в выборку, то выборочная ковариация равна , - результаты наблюдений, включенные в выборку, то выборочная ковариация равна 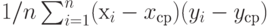 , где , где 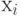 и и 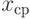 по п.2.2.5, по п.2.2.5, 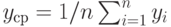
|
| 2.2.12 |
Выборочная ковариационная матрица |
Ковариационная матрица случайного вектора, имеющего эмпирическое распределение |
На главной диагонали выборочной ковариационной матрицы стоят выборочные дисперсии по п.2.2.5, а вне главной диагонали - выборочные ковариации по п.2.2.11 |
| 2.2.13 |
Выборочный коэффициент корреляции
|
Коэффициент корреляции двумерного случайного вектора, имеющего эмпирическое распределение |
Выборочный коэффициент корреляции равен 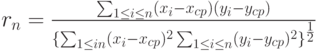 , где , где 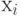 и и 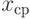 по п.2.2.5, по п.2.2.5,  и и 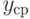 по п.2.2.11. по п.2.2.11. |
| 2.2.14 |
Выборочная корреляционная матрица |
Корреляционная матрица случайного вектора, имеющего эмпирическое распределение |
На главной диагонали выборочной корреляционной матрицы стоят 1, а вне главной диагонали - выборочные коэффициенты корреляции по п.2.2.13. |
| 2.2.15 |
Выборочный коэффициент вариации
|
Отношение выборочного среднего квадратического отклонения к выборочному среднему арифметическому |
Выборочный коэффициент вариации используют, когда результаты наблюдений положительны |
|
|
2.3. Оценивание |
|
| 2.3.1. |
Оценивание |
Приближенное определение интересующей специалиста составляющей вероятностной модели явления (процесса) по выборке |
Составляющими вероятностных моделей могут быть: значение параметра распределения; характеристика распределения (математическое ожидание, коэффициент вариации и др.); функция распределения; плотность вероятности; регрессионная зависимость, и т.д. |
| 2.3.2 |
Оценка |
Результат оценивания по конкретной выборке |
Оценка является статистикой, а потому случайным элементом, в частных случаях - случайной величиной или случайным вектором |
| 2.3.3. |
Точечное оценивание |
Вид оценивания, при котором для оценивания используется одно определенное значение |
|
| 2.3.4. |
Доверительное оценивание |
Вид оценивания, при котором для оценивания используется множество |
Рассматриваемое множество лежит в пространстве возможных состояний оцениваемой составляющей вероятностной модели явления (процесса). |
| 2.3.5 |
Доверительное множество |
Определяемое по выборке множество в пространстве возможных состояний оцениваемой составляющей, используемое при доверительном оценивании |
Доверительное множество является случайным множеством |
| 2.3.6 |
Доверительная вероятность |
Вероятность того, что доверительное множество содержит действительное значение оцениваемой составляющей |
В конкретных задачах оценивания для фиксированных доверительных вероятностей строят соответствующие доверительные множества |
| 2.3.7 |
Доверительный интервал |
Доверительное множество, являющееся интервалом |
Интервалы могут быть как ограниченными, так и неограниченными (лучами). |
| 2.3.8. |
Доверительные границы |
Концы (границы) доверительного интервала
|
|
| 2.3.9. |
Верхняя доверительная граница |
Граница доверительного интервала, являющегося лучом, не ограниченным снизу |
Для доверительного интервала  верхней доверительной границей является число верхней доверительной границей является число  . . |
| 2.3.10 |
Нижняя доверительная граница |
Граница доверительного интервала, являющегося лучом, не ограниченным сверху |
Различие верхних, нижних и двусторонних доверительных границ необходимо учитывать при проведении конкретных расчетов, т.к. часто все виды границ определяются с помощью одних и тех же таблиц |
| 2.3.11 |
Двусторонние доверительные границы |
Границы ограниченного (и сверху, и снизу) доверительного интервала
|
Для двусторонних границ 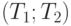 с вероятностью 1 справедливо неравенство с вероятностью 1 справедливо неравенство  . . |
|
|
2.4. Проверка статистических гипотез
|
|
| 2.4.1. |
Статистическая гипотеза
|
Определенное предположение о свойствах распределений случайных элементов, лежащих в основе наблюдаемых случайных явлений (процессов). |
|
| 2.4.2 |
Нулевая гипотеза |
Статистическая гипотеза, подлежащая проверке по статистическим данным (результатам наблюдений, вошедшим в выборку). |
Из возможных статистических гипотез в качестве нулевой выбирают ту, принятие справедливости которой наиболее важно для дальнейших выводов |
| 2.4.3. |
Альтернативная гипотеза |
Статистическая гипотеза, которая считается справедливой, если нулевая гипотеза неверна |
Сокращенная форма - альтернатива |
| 2.4.4. |
Статистический критерий
|
Правило, по которому на основе результатов наблюдений принимается решение о принятии или отклонении нулевой гипотезы |
Принимаемое решение может однозначно определяться по результатам наблюдений (нерандомизированный критерий) или в некоторой степени зависеть от случая (рандомизированный критерий). |
| 2.4.5. |
Статистика критерия |
Статистика, на основе которой сформулировано решающее правило |
Как правило, нерандомизированный статистический критерий основан на статистике критерия, принимающей числовые значения |
| 2.4.6. |
Критическая область статистического критерия
|
Область в пространстве возможных выборок со следующими свойствами: если наблюдаемая выборка принадлежит данной области, то отвергают нулевую гипотезу (и принимают альтернативную), в противном случае ее принимают (и отвергают альтернативную). |
Если статистический критерий основан на статистике критерия, то критическая область статистического критерия однозначно определяется по критической области статистики критерия. Краткая форма: критическая область
|
| 2.4.7. |
Критическая область статистики критерия |
Множество чисел такое, что при попадании в него статистики критерия нулевую гипотезу отвергают, в противном случае принимают |
Краткая форма: критическая область
|
| 2.4.8. |
Критические значения |
Границы (концы) одного или двух интервалов, составляющих критическую область статистики критерия |
Критическими значениями являются одно или два из чисел 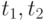 в случае, если критическая область имеет вид в случае, если критическая область имеет вид 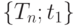 , , 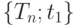 или или  , где , где 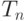 - статистика критерия - статистика критерия |
| 2.4.9 |
Ошибка первого рода |
Ошибка, заключающаяся в том, что нулевую гипотезу отвергают, в то время как в действительности эта гипотеза верна |
|
| 2.4.10 |
Уровень значимости |
Вероятность ошибки первого рода или точная верхняя грань таких вероятностей |
Если нулевая гипотеза является сложной (например, задается с помощью множества параметров 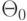 ), то вероятность ошибки первого рода может быть не числом ), то вероятность ошибки первого рода может быть не числом  , а функцией , а функцией 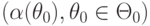 . В качестве уровня значимости берут точную верхнюю грань значений указанной функции: . В качестве уровня значимости берут точную верхнюю грань значений указанной функции: 
|
| 2.4.11 |
Ошибка второго рода
|
Ошибка, заключающаяся в том, что нулевую гипотезу принимают, в то время как в действительности эта гипотеза неверна (а верна альтернативная гипотеза). |
|
| 2.4.12 |
Мощность критерия
|
Вероятность того, что нулевая гипотеза будет отвергнута, если альтернативная гипотеза верна |
Мощность критерия является однозначной действительной функцией, определенной на составляющем альтернативу множестве гипотез, заданном в конкретной задаче статистической проверки гипотез, в частности, на параметрическом множестве, соответствующем альтернативным гипотезам |
| 2.4.13 |
Функция мощности статистического критерия
|
Функция, определяющая вероятность того, что нулевая гипотеза будет отклонена |
Функция мощности критерия задана на множестве всех гипотез, используемых в конкретной задаче статистической проверки гипотез. Сужением ее на нулевую гипотезу является функция, задающая вероятность ошибки первого рода. Сужением ее на альтернативу является мощность критерия
|
| 2.4.14 |
Оперативная характеристика статистического критерия
|
Функция, определяющая вероятность того, что нулевая гипотеза будет принята |
Оперативная характеристика - дополнение до единицы функции мощности статистического критерия
|
| 2.4.15 |
Критерий согласия |
Критерий проверки гипотезы согласия, т.е. того, что функция распределения результатов наблюдения, включенных в простую случайную выборку, совпадает с заданной или входит в заданное параметрическое семейство |
|
| 2.4.16 |
Критерий однородности |
Критерий для проверки гипотезы о том, что функции распределений результатов наблюдений из двух или нескольких независимых простых случайных выборок совпадают (абсолютная однородность) или отдельные их характеристики совпадают (однородность в смысле математических ожиданий, коэффициентов вариации и т.д.). |
Рассматривают также критерии независимости, симметрии, случайности, отбраковки и др |
| 2.4.17 |
Номинальный (заданный) уровень значимости |
Число, используемое в статистических таблицах, с помощью которого выбирают критическое значение статистики критерия при проверке статистической гипотезы |
Номинальный (заданный) уровень значимости обычно берут равным 0,1; 0,05; 0,01. |
| 2.4.18 |
Реальный (истинный) уровень значимости |
Уровень значимости статистического критерия, выбранного по номинальному уровню значимости |
Из-за дискретности распределения статистики критерия реальный уровень значимости может быть в несколько раз меньше номинального |
| 2.4.19 |
Достигаемый уровень значимости |
Случайная величина, равная вероятности попадания статистики критерия в критическую область, заданную рассчитанным по выборке значением статистики критерия |
Для критической области вида 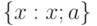 достигаемый уровень значимости есть достигаемый уровень значимости есть 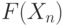 , где , где 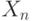 - рассчитанное по выборке значение статистики критерия - рассчитанное по выборке значение статистики критерия  , а , а 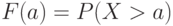 - дополнение до 1 функции распределения статистики критерия - дополнение до 1 функции распределения статистики критерия  . Достигаемый уровень значимости - это вероятность того, что статистика критерия . Достигаемый уровень значимости - это вероятность того, что статистика критерия 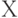 в новом независимом эксперименте примет значение большее, чем при расчете по конкретной выборке, т.е. большее, чем в новом независимом эксперименте примет значение большее, чем при расчете по конкретной выборке, т.е. большее, чем 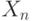
|
| 2.4.20 |
Независимые выборки |
Выборки, объединение элементов которых моделируется набором независимых (в совокупности) случайных элементов |
См. п.1.1.11. |
 и
и  может быть обозначена четырьмя способами - крестиком (т.е.
может быть обозначена четырьмя способами - крестиком (т.е.  ), точкой
), точкой 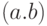 , отсутствием знака между сомножителями
, отсутствием знака между сомножителями 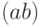 или звездочкой, как при программировании
или звездочкой, как при программировании  . Случайные величины обозначают либо латинскими буквами, либо греческими. Для математического ожидания используют либо символ
. Случайные величины обозначают либо латинскими буквами, либо греческими. Для математического ожидания используют либо символ  , либо символ
, либо символ  , и т.п.. Обычно можно без труда понять, о чем идет речь.
, и т.п.. Обычно можно без труда понять, о чем идет речь.
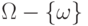 лежит в основе
лежит в основе  -алгебру
-алгебру 
 , определенная на всех случайных событиях и такая, что
, определенная на всех случайных событиях и такая, что 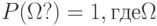 ? - пространство
? - пространство  его вероятность
его вероятность 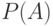 . Термин "мера" понимают в смысле математической теории меры. Синонимы: вероятностное распределение, распределение вероятностей, распределение, вероятность на пространстве
. Термин "мера" понимают в смысле математической теории меры. Синонимы: вероятностное распределение, распределение вероятностей, распределение, вероятность на пространстве 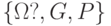 пространства
пространства  ?, класса случайных событий
?, класса случайных событий 
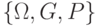 , стремится к вероятности этого события
, стремится к вероятности этого события 
 ,
,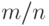 - частота,
- частота,  - вероятность события
- вероятность события  - число повторений. Это свойство нельзя принимать за определение вероятности события в математической теории вероятностей. Оно указывает способ оценивания вероятности по опытным данным.
- число повторений. Это свойство нельзя принимать за определение вероятности события в математической теории вероятностей. Оно указывает способ оценивания вероятности по опытным данным. и
и  являются независимыми, если
являются независимыми, если 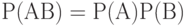 , где
, где 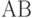 -
- 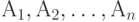 называются независимыми (в совокупности), если
называются независимыми (в совокупности), если  и аналогичные равенства справедливы для всех поднаборов этих событий
и аналогичные равенства справедливы для всех поднаборов этих событий 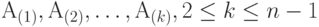
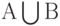 в теории вероятностей по традиции эквивалентно понятию произведения событий
в теории вероятностей по традиции эквивалентно понятию произведения событий  принимает значения в измеримом пространстве
принимает значения в измеримом пространстве 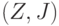 , где
, где  - пространство значений
- пространство значений 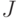 - класс измеримых подмножеств
- класс измеримых подмножеств  множество
множество 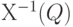 является случайным событием.
является случайным событием.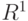 , то случайный элемент
, то случайный элемент 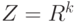 - конечномерное векторное пространство размерности
- конечномерное векторное пространство размерности 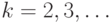 , то случайный элемент
, то случайный элемент ![P_1:J -\to [0,1]](/sites/default/files/tex_cache/bfc756bbd0cbecf84df5712578077d16.png) задается формулой
задается формулой 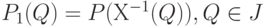 .
.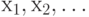 , полностью описывается числами
, полностью описывается числами  , причем
, причем 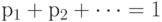 .
. -мерного параметра" часто говорят "зависимость от k параметров".
-мерного параметра" часто говорят "зависимость от k параметров".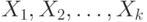 со значениями в измеримых пространствах
со значениями в измеримых пространствах 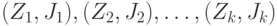 соответственно называются независимыми, если для любых
соответственно называются независимыми, если для любых 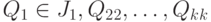 имеем
имеем  .
.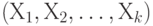 равна произведению плотностей вероятностей случайных величин
равна произведению плотностей вероятностей случайных величин 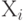 , т.е.
, т.е.  . Результаты экспериментов, которые проведены независимо друг от друга, как правило, моделируются с помощью независимых случайных величин.
. Результаты экспериментов, которые проведены независимо друг от друга, как правило, моделируются с помощью независимых случайных величин.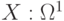 является случайной величиной, если для любого
является случайной величиной, если для любого 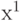 множество
множество  является случайным событием. Случайная величина - это случайный элемент со значениями в
является случайным событием. Случайная величина - это случайный элемент со значениями в  вероятность того, что случайная величина
вероятность того, что случайная величина 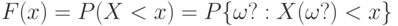 . Функция распределения непрерывна слева. Примечание. Иногда функцию распределения определяют как
. Функция распределения непрерывна слева. Примечание. Иногда функцию распределения определяют как 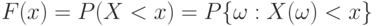 . Тогда она непрерывна справа
. Тогда она непрерывна справа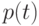 такая, что
такая, что  , при всех
, при всех  - функция распределения рассматриваемой случайной величины
- функция распределения рассматриваемой случайной величины непрерывна
непрерывна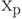 -
- 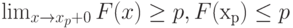 . Может случиться, что вышеуказанное условие выполняется для всех значений
. Может случиться, что вышеуказанное условие выполняется для всех значений  .
Примечание. Одни авторы употребляют термин "
.
Примечание. Одни авторы употребляют термин "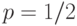 .
. , т.е.
, т.е. 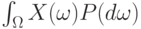
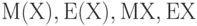 и др. Рекомендуемое обозначение:
и др. Рекомендуемое обозначение: 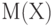 . При этом
. При этом 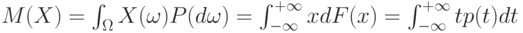 , где
, где 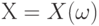 . Математическое ожидание существует не для всех случайных величин
. Математическое ожидание существует не для всех случайных величин  )
)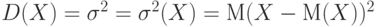 . Дисперсия равна 0 тогда и только тогда когда
. Дисперсия равна 0 тогда и только тогда когда 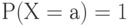 для некоторого а
для некоторого а (случайной величины
(случайной величины 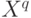
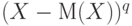 , где М(Х) - математическое ожидание
, где М(Х) - математическое ожидание  при каждом
при каждом  равная математическому ожиданию случайной величины
равная математическому ожиданию случайной величины  , где
, где  -
-  - основание натуральных логарифмов
- основание натуральных логарифмов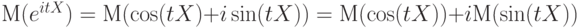 .
.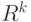 .
.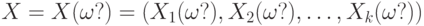 , где
, где 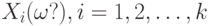 , - случайные величины, заданные на одном и том же вероятностном пространстве
, - случайные величины, заданные на одном и том же вероятностном пространстве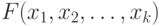 случайного вектора
случайного вектора  удовлетворяет равенству
удовлетворяет равенству  .
.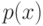 такая, что
такая, что  для случайного вектора
для случайного вектора 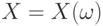 и любого борелевского подмножества
и любого борелевского подмножества 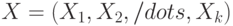 есть
есть 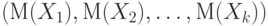 , где
, где 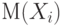 - математическое ожидание случайной величины
- математическое ожидание случайной величины  , являющейся
, являющейся 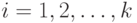 .
. называется математическое ожидание случайной величины
называется математическое ожидание случайной величины 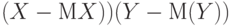 , где
, где  и
и 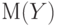 - математические ожидания случайных величин
- математические ожидания случайных величин  .
.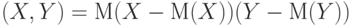 ; если
; если 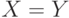 , то
, то 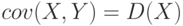 - дисперсия
- дисперсия 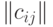 порядка
порядка 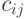 - ковариация двумерного вектора
- ковариация двумерного вектора 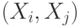 , где
, где  - компоненты случайного вектора
- компоненты случайного вектора 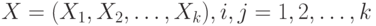 .
.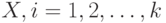 .
.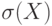 и
и 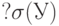 случайных величин
случайных величин 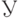 .
.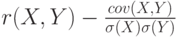 . Если
. Если  . Верно и обратное: если
. Верно и обратное: если 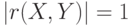 , то
, то 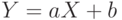 ..
..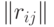 порядка
порядка 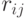 -
- 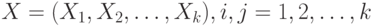 .
. - число объектов конечной совокупности, то для получения случайной выборки объема
- число объектов конечной совокупности, то для получения случайной выборки объема  , отбор объектов для проведения наблюдений должен проводиться так, чтобы любой набор из
, отбор объектов для проведения наблюдений должен проводиться так, чтобы любой набор из  !, т.е. обратной величине к числу сочетаний из
!, т.е. обратной величине к числу сочетаний из 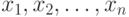 , то эмпирическое распределение - это распределение случайной величины
, то эмпирическое распределение - это распределение случайной величины 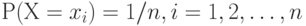 . Если несколько результатов наблюдений совпадают:
. Если несколько результатов наблюдений совпадают:  , то полагают
, то полагают  .
.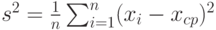 , где
, где 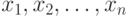 - результаты наблюдений, включенные в выборку;
- результаты наблюдений, включенные в выборку; 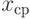 -
- 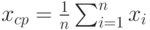 . Выборочная дисперсия равна дисперсии случайной величины, имеющей эмпирическое распределение
. Выборочная дисперсия равна дисперсии случайной величины, имеющей эмпирическое распределение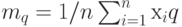 , где
, где 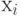 по п.2.2.5.
по п.2.2.5. где
где 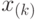 в вариационном ряду, полученном из выборки объема
в вариационном ряду, полученном из выборки объема 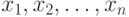 расположены в порядке неубывания:
расположены в порядке неубывания:  .
.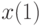 и
и 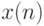 - первая и
- первая и 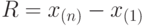 .
.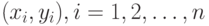 , - результаты наблюдений, включенные в выборку, то выборочная ковариация равна
, - результаты наблюдений, включенные в выборку, то выборочная ковариация равна 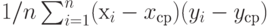 , где
, где 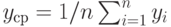
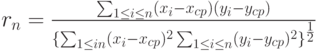 , где
, где  и
и 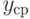 по п.2.2.11.
по п.2.2.11. верхней доверительной границей является число
верхней доверительной границей является число 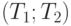 с вероятностью 1 справедливо неравенство
с вероятностью 1 справедливо неравенство  .
.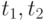 в случае, если
в случае, если 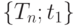 ,
, 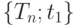 или
или  , где
, где 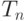 - статистика критерия
- статистика критерия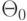 ), то вероятность ошибки первого рода может быть не числом
), то вероятность ошибки первого рода может быть не числом  , а функцией
, а функцией 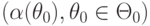 . В качестве уровня значимости берут точную верхнюю грань значений указанной функции:
. В качестве уровня значимости берут точную верхнюю грань значений указанной функции: 
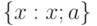 достигаемый уровень значимости есть
достигаемый уровень значимости есть 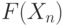 , где
, где 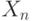 - рассчитанное по выборке значение статистики критерия
- рассчитанное по выборке значение статистики критерия 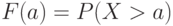 - дополнение до 1 функции распределения статистики критерия
- дополнение до 1 функции распределения статистики критерия 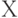 в новом независимом эксперименте примет значение большее, чем при расчете по конкретной выборке, т.е. большее, чем
в новом независимом эксперименте примет значение большее, чем при расчете по конкретной выборке, т.е. большее, чем