|
Здравствуйте! Записался на ваш курс, но не понимаю как произвести оплату. Надо ли писать заявление и, если да, то куда отправлять? как я получу диплом о профессиональной переподготовке? |
Корректность и устойчивость программных систем
Проект к данной лекции Вы можете скачать ![]() здесь.
здесь.
Корректность и устойчивость
Корректность и устойчивость - два основных качества программной системы, без которых все остальные ее достоинства не имеют особого смысла.
Корректность - это способность программной системы работать в строгом соответствии со своей спецификацией. Отладка - процесс, направленный на достижение корректности.
Понятие корректности программной системы имеет смысл только тогда, когда задана ее спецификация. В зависимости от того, как формализуется спецификация, уточняется понятие корректности.
Во время работы системы могут возникать ситуации, которые выходят за пределы, предусмотренные спецификацией. Такие ситуации называются исключительными.
Устойчивость - это способность программной системы должным образом реагировать на исключительные ситуации. Обработка исключительных ситуаций - процесс, направленный на достижение устойчивости.
Почему так трудно создавать корректные и устойчивые программные системы? Все дело в сложности разрабатываемых систем. Когда в 60-х годах прошлого века фирмой IBM создавалась операционная система OS-360, то на ее создание потребовалось 5000 человеко-лет, и проект по сложности сравнивался с проектом высадки первого человека на Луну. Сложность нынешних сетевых операционных систем, систем управления хранилищами данных, прикладных систем программирования на порядок превосходит сложность OS-360, так что, несмотря на прогресс, достигнутый в области технологии программирования, проблемы, стоящие перед разработчиками, не стали проще.
Жизненный цикл программной системы
Под " жизненным циклом " понимается период от замысла программного продукта до его "кончины". Обычно рассматриваются следующие фазы этого процесса:
Проектирование  Разработка
Разработка  Развертывание и Сопровождение
Развертывание и Сопровождение
Все это называется циклом, поскольку после каждой фазы возможен возврат к предыдущим этапам. В объектной технологии этот процесс является бесшовным, все этапы которого тесно переплетены. Не следует рассматривать его как однонаправленный - от проектирования к сопровождению. Чаще всего, ситуация обратная: уже существующая реализация системы, прошедшая сопровождение, и существующие библиотеки компонентов оказывают решающее влияние на то, какой будет новая система, каковы будут ее спецификации.
Вот некоторые типовые правила, характерные для процесса разработки ПО.
- Уделяйте этапу проектирования самое пристальное внимание. Успех дела во многом определяется первым этапом. Нет смысла торопиться с переходом на последующие этапы, пока не составлены ясные и четкие спецификации. Ошибки этого этапа- самые дорогие и трудно исправляемые.
- Помните о тех, для кого разрабатывается программный продукт. Идите "в люди", чтобы понять, что нужно делать. Вместе с тем не следует полностью полагаться на пользователей - их опыт консервативен, новые идеи могут часто приходить от разработчиков, а не от пользователей.
- Разработка не начинается "с нуля". Только используя уже готовые компоненты, можно своевременно создать новую систему. Работая над проектом, думайте о будущем создавайте компоненты, допускающие их повторное использование в других проектах.
- Создавайте как можно раньше прототип своей системы и передавайте его пользователям в опытную эксплуатацию. Это поможет устранить множество недостатков и ошибок в заключительной версии программного продукта.
- Какие бы хорошие спецификации не были написаны, какими бы хорошими технологиями и инструментами не пользовались разработчики, какими бы профессионалами они ни были - этого еще не достаточно для успеха дела. Необходимым условием является управление проектом, наличие специальных средств управления. Но и этого не достаточно. Третьим важным фактором является существование команды. Коллектив разработчиков должен представлять собой единый коллектив. Умение работать в команде так же важно, как и профессиональные навыки разработчика.
Три закона программотехники
Первый закон (закон для разработчика)
Корректность системы - недостижима. Каждая последняя найденная ошибка является предпоследней.
Этот закон отражает сложность нетривиальных систем. Разработчик всегда должен быть готов к тому, что в работающей системе имеются ситуации, в которых система работает не в точном соответствии со своей спецификацией, так что от него может требоваться очередное изменение либо системы, либо ее спецификации. Как следствие, отсюда вытекает важность обеспечения устойчивости системы.
Второй закон (закон для пользователя)
Не бывает некорректных систем. Каждая появляющаяся ошибка при эксплуатации системы - это следствие незнания спецификации системы.
Есть два объяснения справедливости второго закона. Несерьезное объяснение состоит в том, что любая система, что бы она ни делала, при любом постусловии корректна по отношению к предусловию False, поскольку невозможно подобрать ни один набор входных данных, удовлетворяющих этому предусловию. Так что все системы корректны, если задать False в качестве их предусловия. Если вам пришлось столкнуться с системой, предусловие которой близко к False, то лучшее, что можно сделать, это отложить ее в сторону и найти другую.
Более поучительна реальная ситуация, подтверждающая второй закон и рассказанная мне в былые годы Виталием Кауфманом - специалистом по тестированию трансляторов. В одной серьезной организации была разработана серьезная прикладная система, имеющая для них большое значение. К сожалению, при ее эксплуатации сплошь и рядом возникали ошибки, из-за которых организация вынуждена была отказаться от использования системы. Разработчики обратились к нему за помощью. Он, исследуя систему, не внес в нее ни строчки кода. Единственное, что он сделал, это вместе с разработчиками описал точную спецификацию системы, благодаря чему стала возможной нормальная эксплуатация.
Обратите внимание на философию, характерную для этих законов: при возникновении ошибки разработчик и пользователь должны винить себя, а не кивать друг на друга. Так что часто встречающиеся фразы: "Ох, уж эта фирма Чейтософт, вечно у них ошибки!" характеризует, мягко говоря, непрофессионализм пользователя.
Третий закон (закон чечако)
Если спецификацию можно нарушить, она будет нарушена. Новичок (чечако) способен "подвесить" любую систему.
Неквалифицированный пользователь в любом контексте всегда способен выбрать наименее подходящее действие, явно не удовлетворяющее спецификации, которая ориентирована на "разумное" поведение пользователей. Полезным практическим следствием этого закона является привлечение к этапу тестирования системы неквалифицированного пользователя - "человека с улицы".
Надежный код
Что должно делать для создания корректного и устойчивого программного продукта? Как минимум, необходимо:
- создавать код, корректность которого предусматривается с самого начала;
- отладить этот код;
- предусмотреть в нем обработку исключительных ситуаций.
Создание надежного кода
Большинство вопросов, затрагиваемых в этой лекции, в том числе и проблемы создания надежного кода, заслуживают отдельного и глубокого рассмотрения. К сожалению, придется ограничиться лишь высказыванием ряда тезисов.
Для повышения надежности нужно уменьшить сложность системы, и главное в этом процессе - это повторное использование. В идеале большая часть системы должна быть собрана из уже готовых компонентов. Объектная технология проектирования вносит свой вклад в повышение надежности кода. Наследование и универсализация позволяют, не изменяя уже существующие классы, создать новые классы, новые типы данных, придающие проектируемой системе новые свойства при минимальных добавлениях нового кода. Статический контроль типов дает возможность выявить многие ошибки еще на этапе компиляции. Динамическое связывание и полиморфизм позволяют автоматически включать объекты классов-потомков в уже существующие схемы работы - методы родителя могут вызывать методы потомков, не зная о появлении этих новых потомков. Автоматическая сборка мусора дает возможность снять с разработчика обязанности управления освобождением памяти и предотвратить появление крайне неприятных и опасных ошибок, связанных с некорректным удалением объектов.
Крайне важную роль в создании надежного кода играют спецификации методов класса, класса в целом, системы классов. Спецификации являются частью документации, встроенной в проект, и вообще важной его частью. Их существование облегчает не только создание корректного кода, соответствующего спецификации, но и создание системы тестов, проверяющих корректность кода. Существуют специальные инструментальные средства, поддерживающие автоматическое создание тестов на основе спецификаций. Незаменима роль спецификаций на этапе сопровождения и повторного использования компонентов. Невозможно повторно использовать компонент, если у него нет ясной и полной спецификации.
Написать программную систему нетрудно. Это может сделать каждый. Значительно сложнее написать ее так, чтобы она корректно решала задачи пользователя. Корректность системы - это не внутреннее понятие, подлежащее определению в терминах самой системы. Корректность определяется по отношению к внешним спецификациям системы. Если нет спецификаций, то говорить о корректности "некорректно".
Корректность методов
Спецификации метода можно задавать по-разному. Определим их здесь через понятия предусловий и постусловий метода, используя символику триад Xoара, введенных Чарльзом Энтони Хоаром - выдающимся программистом и ученым.
Пусть P(x,z) - метод P с входными аргументами x и выходными z. Пусть Q(y) - некоторое логическое условие (предикат) над переменными y. Предусловием метода P(x,z) будем называть предикат Pre(x), заданный на входах метода. Постусловием метода P(x,z) будем называть предикат Post(x,z), связывающий входы и выходы метода. Для простоты будем полагать, что метод P не изменяет своих входов x в процессе своей работы. Теперь несколько определений:
Определение 1 ( частичной корректности ). Метод P(x,z) корректен (частично, или условно) по отношению к предусловию Pre(x) и постусловию Post(x,z), если из истинности предиката Pre(x) следует, что для метода P(x,z), запущенного на входе x, гарантируется выполнение предиката Post(x,z) при условии завершения метода на этом входе.
Условие частичной корректности записывается в виде триады Хоара, связывающей метод с его предусловием и постусловием:
[Pre(x)]P(x,z)[Post(x,z)]
Определение 2 ( полной корректности ). Метод P(x,z) корректен (полностью, или тотально) по отношению к предусловию Pre(x) и постусловию Post(x,z), если из истинности предиката Pre(x) следует, что для метода P(x,z), запущенного на входе x, гарантируется его завершение и выполнение предиката Post(x,z) в точке завершения метода.
Условие полной корректности записывается в виде триады Хоара, связывающей программу с ее предусловием и постусловием:
{Pre(x)}P(x,z){Post(x,z)}Доказательство полной корректности обычно состоит из двух независимых этапов - доказательства частичной корректности и доказательства завершаемости программы. Заметьте, полностью корректная программа, которая запущена на входе, не удовлетворяющем ее предусловию, вправе зацикливаться, вправе возвращать любой результат. Любая программа корректна по отношению к предусловию, заданному тождественно ложным предикатом False. Любая завершающаяся программа корректна по отношению к постусловию, заданному тождественно истинным предикатом True.
Корректная программа говорит своим клиентам: если вы хотите вызвать меня и ждете гарантии выполнения постусловия после моего завершения, то будьте добры гарантировать выполнение предусловия на входе. Задание предусловий и постусловий методов - это такая же важная часть работы программиста, как и написание самого метода. На языке C# пред- и постусловия обычно задаются в теге summary, предшествующем методу, и являются частью XML-отчета. К сожалению, технология работы в Visual Studio не предусматривает возможности автоматической проверки предусловия перед вызовом метода и проверки постусловия после его завершения с выбрасыванием исключений в случае их невыполнения. Программисты, для которых требование корректности является важнейшим условием качества их работы, сами встраивают такую проверку в свои программы. Как правило, подобная проверка обязательна на этапе отладки и может быть отключена в готовой системе, в корректности которой программист уже уверен. А вот проверку предусловий важно оставлять и в готовой системе, поскольку истинность предусловий должен гарантировать не разработчик метода, а клиент, вызывающий метод. Клиентам же свойственно ошибаться и вызывать метод в неподходящих условиях.
Формальное доказательство корректности метода - задача ничуть не проще, чем написание корректной программы. Но вот парадокс. Чем сложнее метод, его алгоритм, а следовательно, и само доказательство, тем важнее использовать понятия предусловий и постусловий, понятия инвариантов циклов в процессе разработки метода. Рассмотрение этих понятий параллельно с разработкой метода может существенно облегчить построение корректного метода.
Инварианты и варианты цикла
Циклы, как правило, являются наиболее сложной частью метода, большинство ошибок связано именно с ними. При написании корректно работающих циклов крайне важно понимать и использовать понятия инварианта и варианта цикла. Без этих понятий не обходится формальное доказательство корректности циклов. Но и неформальное понимание правильности работы программы основано на этих понятиях.
Рассмотрим цикл в форме, к которой можно привести все виды циклов:
Init(x,z); while(B)S(x,z);
Здесь B - условие цикла while, S - его тело, а Init - группа предшествующих операторов, задающая инициализацию цикла. Реально ни один цикл не обходится без инициализирующей части. Синтаксически было бы правильно, чтобы Init являлся бы формальной частью оператора цикла. В операторе for это частично сделано - инициализация счетчиков является частью цикла.
Определение 3 ( инварианта цикла ). Предикат Inv(x, z) называется инвариантом цикла while, если истинна следующая триада Хоара:
{Inv(x, z)& B}S(x,z){Inv(x,z)}Содержательно это означает, что из истинности инварианта цикла до начала выполнения тела цикла и из истинности условия цикла, гарантирующего выполнение тела, следует истинность инварианта после выполнения тела цикла. Сколько бы раз ни выполнялось тело цикла, его инвариант остается истинным.
Для любого цикла можно написать сколь угодно много инвариантов. Любое тождественное условие (2*2 =4) является инвариантом любого цикла. Поэтому среди инвариантов выделяются так называемые подходящие инварианты цикла. Они называются подходящими, поскольку позволяют доказать корректность цикла по отношению к его пред- и постусловиям. Как доказать корректность цикла? Рассмотрим соответствующую триаду:
{Pre(x)} Init(x,z); while(B)S(x,z);{Post(x,z)}Доказательство разбивается на три этапа. Вначале доказываем истинность триады:
(*) {Pre(x)} Init(x,z){RealInv(x,z)}Содержательно это означает, что предикат RealInv становится истинным после выполнения инициализирующей части. Далее доказывается, что RealInv является инвариантом цикла:
(**) {RealInv(x, z)& B} S(x,z){ RealInv(x,z)}На последнем шаге доказывается, что наш инвариант обеспечивает решение задачи после завершения цикла:
(***) ~B & RealInv(x, z) -> Post(x,z)
Это означает, что из истинности инварианта и условия завершения цикла следует требуемое постусловие.
Определение 4 ( подходящего инварианта ). Предикат RealInv, удовлетворяющий условиям (*), (**), (***) называется подходящим инвариантом цикла.
С циклом связано еще одно важное понятие - варианта цикла, используемое для доказательства завершаемости цикла.
Определение 5 ( варианта цикла ). Целочисленное неотрицательное выражение Var(x, z) называется вариантом цикла, если выполняется следующая триада:
{(Var(x,z)= n) & B} S(x,z){(Var(x,z)= m) & (m < n)}Содержательно это означает, что каждое выполнение тела цикла приводит к уменьшению значения его варианта. После конечного числа шагов вариант достигает своей нижней границы, и цикл завершается. Простейшим примером варианта цикла является выражение n - i для цикла
for(i = 1; i <= n; i++) S(x, z);.
Пользоваться инвариантами и вариантами цикла нужно не только и не столько для того, чтобы проводить формальное доказательство корректности циклов. Они способствуют написанию корректных циклов. Правило корректного программирования гласит: "При написании каждого цикла программист должен определить его походящий инвариант и вариант". Задание предусловий, постусловий, вариантов и инвариантов циклов является такой же частью процесса разработки корректного метода, как и написание самого кода.
Трудно ли строить инварианты и варианты цикла? Необходима некоторая практика, но обычно понимание алгоритма означает и понимание инвариантов, обеспечивающих корректность работы алгоритма. Рассмотрим простой пример класса, методы которого вычисляют различные суммы элементов массива.
class Simple
{
double[] x;
public Simple(double[] x)
{
this.x = x;
}
public double Sum1()
{
//Init:
double S = 0;
int i = 0;
while (i < x.Length)
{
S += x[i]; i++;
}
return S;
}
public double Sum2()
{
//Init:
double S = 0;
int i = 0;
while (i < x.Length -1)
{
i++; S += x[i];
}
return S;
}
public double Sum3()
{
//Init:
double S = 0;
int i = 0;
while (i < x.Length -1)
{
S += x[i]; i++;
}
return S;
}
public double Sum4()
{
//Init:
double S = x[0];
int i = 1;
while (i < x.Length)
{
S += x[i]; i++;
}
return S;
}
}Ограничимся рассмотрением метода Sum1. В качестве предусловия выберем следующий предикат Pre(x):
Pre(x): (x - массив элементов типа double) && ( x.Length >= 0)
В качестве подходящего инварианта цикла выберем предикат Inv(x, S, i):
![Inv(x,S,i): |left ( S = \sum\limits_{k=0}^{i-1}{x[k]} \right ) & & (i \le x.Length)](/sites/default/files/tex_cache/dcb9af523d28ac3765b782415f731b0e.png)
Содержательно инвариант говорит, что на каждом шаге цикла S представляет сумму элементов начального отрезка массива. В качестве постусловия метода Post(x, S) выберем предикат:
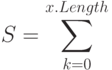
Постусловие отражает требование к методу - по его завершению S должно представлять сумму элементов массива. Нетрудно строго доказать, что метод Sum1 корректен по отношению к заданным спецификациям - предусловию и постусловию. Другими словами, справедлива истинность триады Хоара:
{Pre(x)} Sum1{Post(x, S)}Формального доказательства приводить не буду. Понятно, что инициализация обеспечивает истинность инварианта, поскольку по определению для пустого множества функция ? равна нулю. Выполнение тела цикла сохраняет истинность инварианта, а из условия завершаемости цикла и истинности инварианта следует предусловие. В момент завершения цикла счетчик цикла i принимает значение x.Length.
Очевидно, что имеет место завершаемость цикла, вариантом которого является выражение x.Length - i.
Что должен понимать начинающий программист, осваивающий азы программирования, в задачу которого входит написание программы вычисления суммы элементов масива? Он должен понимать, что на каждом шаге выполнения цикла переменная S представляет сумму начального отрезка массива. Вначале отрезок пуст и сумма равна нулю. Когда цикл завершается, начальный отрезок совпадает со всем массивом. В этом суть алгоритма, и инвариант отражает эту суть.
Метод Sum4 также корректен по отношению к тем же предикатам. Небольшое отличие существует в предусловии, требующем, чтобы массив был не пуст. Методы Sum2 и Sum3 вычисляют сумму части массива и не гарантируют корректности по отношению к заданным спецификациям. Хотя, конечно, можно изменить предусловие и постусловие так, чтобы методы были корректны по отношению к ним. Другое дело, устроит ли пользователя такая спецификация. Еще раз повторяю, без спецификации нельзя говорить о корректности.
